Презентация на тему Тригонометрическая окружность

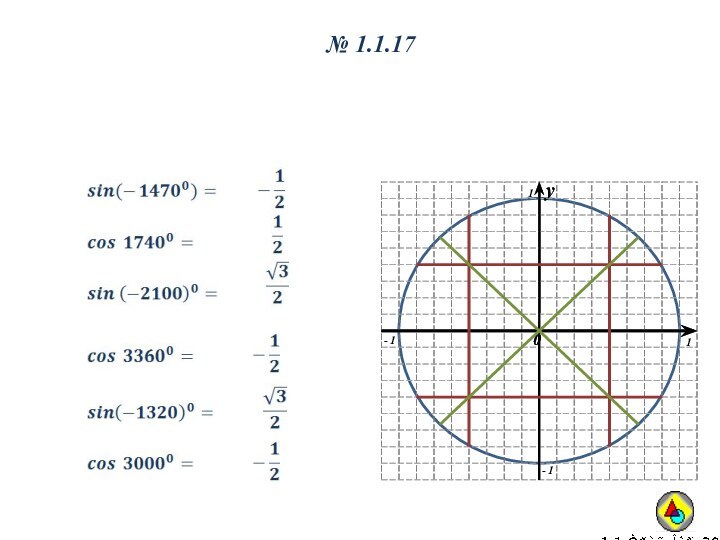
Р240° ϵ
IIIчетверти
в) Р-240° ϵ
II четверти
г) Р125° ϵ
II четверти
д) Р-340°

I четверти

Р-340°

е) Р1040° ϵ

IVчетверти

Р1040°

ж) Р-800° ϵ

IVчетверти

Р-800°

I

II

III

IV

В-540°

В810°

В-1170°

(В1350°)

(В-1260°)

В-1800°

Р30°
б) Р-230°
в) Р-560°
г) Р130°
д) Р-228°

ϵ I четв.;

ϵ III четв.;

ϵ II четв.;

ϵ II четв.;

ϵ II четв.;

ϵ II четв.;

ϵ II четв.;

ϵ IV четв.;

ϵ IV четв.;

и проведем через середины единичных отрезков прямые, параллельные соответствующим

С

D

F

E

Рассмотрим прямоугольные треугольники OCD и OFE.

∆ OCD = ∆ OFE ( по катету и гипотенузе)

Следовательно дуги АС, СF и FM равны между собой и равны 300.

Вся окружность оказалась поделена на двенадцать равных между собой дуг, с градусной мерой 300.

A

M

кратна 300.

x
Р30°
№ 1.1.6
а) 300
Р120°
б) 1200
Р210°
в) 2100
Р330°
г) 3300
Р780°
д) 7800
Р-60°
е) -

Р-120°

ж) – 1200

Р-210°

з) - 2100

Р360°

и) - 3600

кратна 450.

x
Р45°
№ 1.1.7
а) 45 0
Р135°
б) 1350
Р225°
в) 2250
Р315°
г) 3150
Р270°
д) 2700

-1350
Р-60°
е) - 3900
Р150°

– 4050
Р90°

– 7800
Р495°

11700
Р1110°

α =
yα
?
(

xα

xα

;

?

)

yα

yα

xα

cos α =

косинуса, тангенса и котангенса
произвольного угла

котангенса
произвольного угла

∆OCD:
CD= ½; ОС=1
1
Тогда по теореме Пифагора:
OD=

( ; )

; )
∆ OEF = ∆ OCD

( ; )

Рассмотрим ∆ OEF :

Таким образом легко находятся значения синуса, косинуса, тангенса и котангенса углов кратных 300.

OSH, прямоугольный и равнобедренный:
1
OS = 1
По теореме Пифагора:

Тогда SH = OH = .

( ; )

Следовательно, известны

координаты точки S.

существ.
- 1
0
0
не существ.