Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Тригонометрические функции угла

Содержание

Что такое косинус угла ?Это число, которое можно определить следующим образом:Харьковский В.З.
Тригонометрические функции угла(00 – 1800)Харьковский В.З. Что такое косинус угла ?Это число, которое можно определить следующим образом:Харьковский В.З. cos α ≈ 0,410-11-1В прямоугольной системе коодинатпроводим полуокружностьс центром в начале координати Попробуйте теперь сами:выполните чертеж и определите (приближенно) косинус угла 1100Харьковский В.З. cos α ≈ - 0,310-11-1В прямоугольной системе коодинатпроводим полуокружностьс центром в начале Что такое синус угла ?Это число, которое можно определить следующим образом:Харьковский В.З. 10-11-1В прямоугольной системе коодинатпроводим полуокружностьс центром в начале координати радиусом, равным 1Точку, Помните: синус угла – это ордината точки; косинус угла Найдите самостоятельносинус другого угла, например синус угла 1570Харьковский В.З. 10-11-1В прямоугольной системе коодинатпроводим полуокружностьс центром в начале координати радиусом, равным 1Точку, Что такое тангенс угла ?Это число, которое можно определить следующим образом:tg α Что такое котангенс угла ?Это число, которое можно определить следующим образом:сtg α А теперь задания:1. Определите:cos 900sin 900sin 1800cos 1800tg 1800cos 450sin 300tg 600ctg 10-11-10,5Харьковский В.З. Харьковский В.З.Харьковский В.З.
Слайды презентации

Слайд 2 Что такое косинус угла ?
Это число, которое можно

Что такое косинус угла ?Это число, которое можно определить следующим образом:Харьковский В.З.

определить следующим образом:
Харьковский В.З.

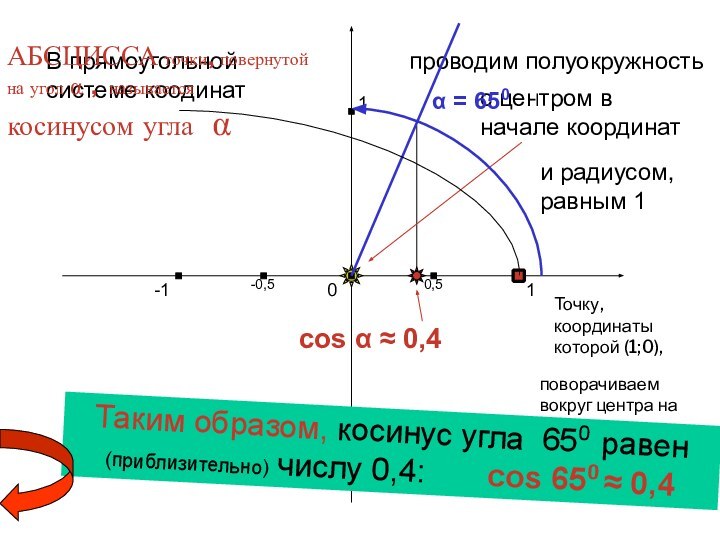
Слайд 3 cos α ≈ 0,4
1


0
-1




1

-1


В прямоугольной системе коодинат
проводим полуокружность
с

cos α ≈ 0,410-11-1В прямоугольной системе коодинатпроводим полуокружностьс центром в начале

центром в начале координат
и радиусом, равным 1

Точку, координаты которой

(1;0),

поворачиваем вокруг центра на угол α

АБСЦИССА точки, повернутой на угол α , называется косинусом угла α

α = 650



0,5

-0,5

Таким образом, косинус угла 650 равен (приблизительно) числу 0,4: cos 650 ≈ 0,4


Харьковский В.З.

Слайд 4 Попробуйте теперь сами:
выполните чертеж и определите (приближенно)
косинус

Попробуйте теперь сами:выполните чертеж и определите (приближенно) косинус угла 1100Харьковский В.З.

угла 1100
Харьковский В.З.

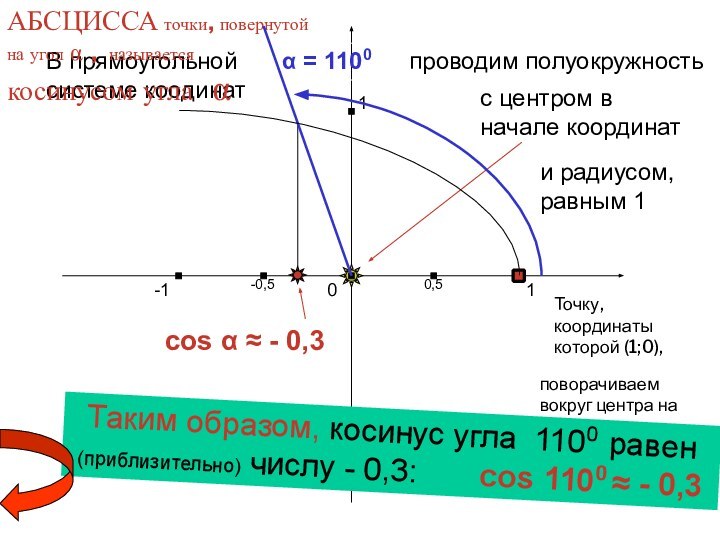
Слайд 5 cos α ≈ - 0,3
1


0
-1




1

-1


В прямоугольной системе коодинат
проводим

cos α ≈ - 0,310-11-1В прямоугольной системе коодинатпроводим полуокружностьс центром в

полуокружность
с центром в начале координат
и радиусом, равным 1

Точку, координаты

которой (1;0),

поворачиваем вокруг центра на угол α

АБСЦИССА точки, повернутой на угол α , называется косинусом угла α

α = 1100



0,5

-0,5

Таким образом, косинус угла 1100 равен (приблизительно) числу - 0,3: cos 1100 ≈ - 0,3


Харьковский В.З.

Слайд 6 Что такое синус угла ?
Это число, которое можно

Что такое синус угла ?Это число, которое можно определить следующим образом:Харьковский В.З.

определить следующим образом:
Харьковский В.З.

Слайд 7 1


0
-1



1

-1


В прямоугольной системе коодинат
проводим полуокружность
с центром в начале

10-11-1В прямоугольной системе коодинатпроводим полуокружностьс центром в начале координати радиусом, равным

координат
и радиусом, равным 1

Точку, координаты которой (1;0),
поворачиваем вокруг

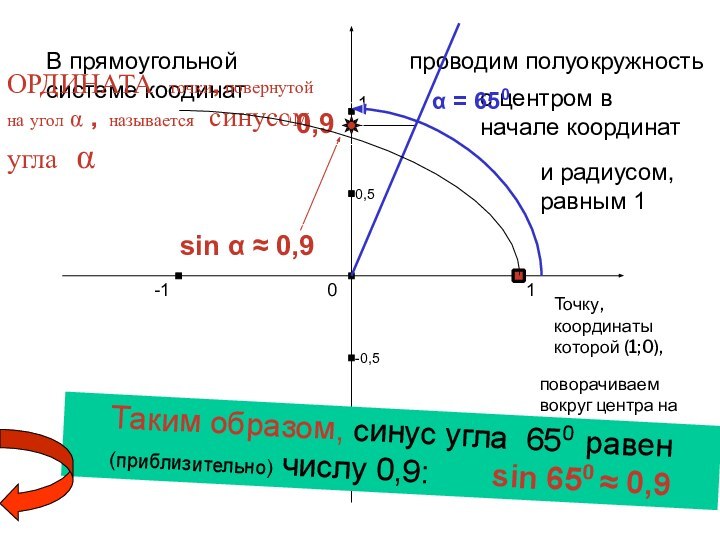
центра на угол α

ОРДИНАТА точки, повернутой на угол α , называется синусом угла α

α = 650



0,5

-0,5

Таким образом, синус угла 650 равен (приблизительно) числу 0,9: sin 650 ≈ 0,9

sin α ≈ 0,9

0,9


Харьковский В.З.

Слайд 8 Помните: синус угла – это ордината точки; косинус угла

Помните: синус угла – это ордината точки; косинус угла – это абсцисса точкиХарьковский В.З.

– это абсцисса точки
Харьковский В.З.

Слайд 9 Найдите самостоятельно
синус другого угла, например
синус угла 1570
Харьковский

Найдите самостоятельносинус другого угла, например синус угла 1570Харьковский В.З.

В.З.

Слайд 10 1


0
-1



1

-1


В прямоугольной системе коодинат
проводим полуокружность
с центром в начале

10-11-1В прямоугольной системе коодинатпроводим полуокружностьс центром в начале координати радиусом, равным

координат
и радиусом, равным 1

Точку, координаты которой (1;0),
поворачиваем вокруг

центра на угол α

ОРДИНАТА точки, повернутой на угол α , называется синусом угла α

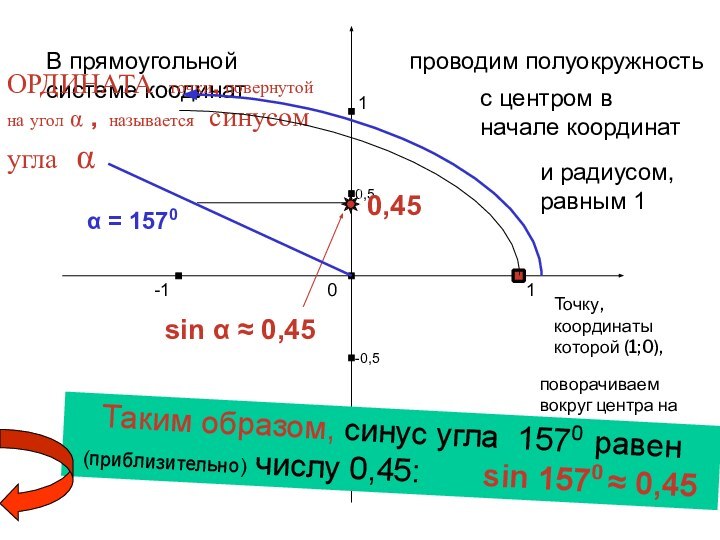
α = 1570



0,5

-0,5

Таким образом, синус угла 1570 равен (приблизительно) числу 0,45: sin 1570 ≈ 0,45

sin α ≈ 0,45

0,45


Харьковский В.З.

Слайд 11 Что такое тангенс угла ?
Это число, которое можно

Что такое тангенс угла ?Это число, которое можно определить следующим образом:tg

определить следующим образом:
tg α =
sin α
cos α
Харьковский

В.З.

Слайд 12 Что такое котангенс угла ?
Это число, которое можно

Что такое котангенс угла ?Это число, которое можно определить следующим образом:сtg

определить следующим образом:
сtg α =
cos α
sin α
Харьковский

В.З.

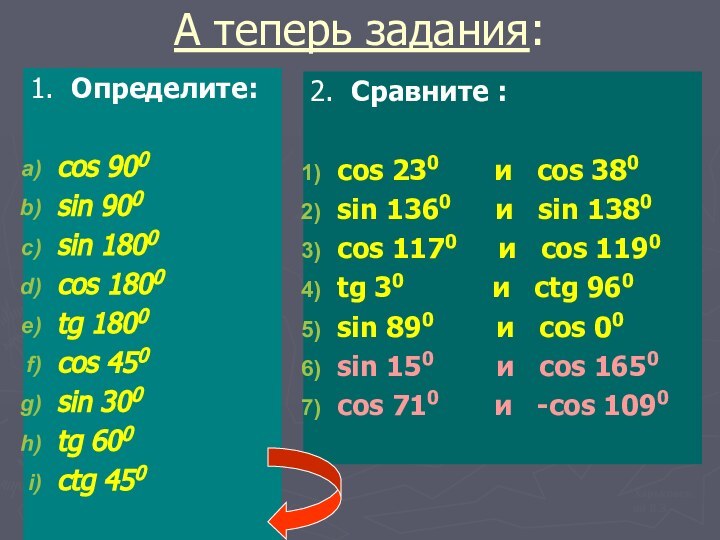
Слайд 13 А теперь задания:
1. Определите:

cos 900
sin 900
sin 1800
cos 1800
tg

А теперь задания:1. Определите:cos 900sin 900sin 1800cos 1800tg 1800cos 450sin 300tg

1800
cos 450
sin 300
tg 600
ctg 450


2. Сравните :

cos 230

и cos 380
sin 1360 и sin 1380
cos 1170 и cos 1190
tg 30 и ctg 960
sin 890 и cos 00
sin 150 и cos 1650
cos 710 и -cos 1090


Харьковский В.З.

Слайд 14 1


0
-1



1

-1



0,5
Харьковский В.З.

10-11-10,5Харьковский В.З.
  • Имя файла: trigonometricheskie-funktsii-ugla.pptx
  • Количество просмотров: 114
  • Количество скачиваний: 0
- Предыдущая Помоги первокласснику безопасно прийти в школу
Следующая - Новгород-Сіверське медичне училище

Похожие презентации

НОД по ФЭМП в средней группе план-конспект занятия по математике (средняя группа) НОД по ФЭМП в средней группе план-конспект занятия по математике (средняя группа) 174
Уменьшаемое. Вычитаемое. Разность. план-конспект урока по математике (1 класс) Уменьшаемое. Вычитаемое. Разность. план-конспект урока по математике (1 класс) 119
Способы нахождения корней многочленов Способы нахождения корней многочленов 153
Решение заданий ЕГЭ математика В6 Решение заданий ЕГЭ математика В6 122
Решение иррациональных неравенств (11 класс) Решение иррациональных неравенств (11 класс) 120
Мастер-класс Танграм презентация к уроку по математике Мастер-класс Танграм презентация к уроку по математике 111
Площадь прямоугольника Площадь прямоугольника 101
prezentaciya 2 0 prezentaciya 2 0 111
Презентация по математике по теме Прямоугольник Презентация по математике по теме Прямоугольник 104
Вероятностные задачи в ГИА 9,11 классах Вероятностные задачи в ГИА 9,11 классах 111
Интерактивный тренажер по теме Сравни величины. Единицы времени Интерактивный тренажер по теме Сравни величины. Единицы времени 110
ПРЕЗЕНТАЦИЯ: Формирование навыков логического мышления, внимания, памяти через занимательные игры математического содержания. презентация к уроку по математике (подготовительная группа) по теме ПРЕЗЕНТАЦИЯ: Формирование навыков логического мышления, внимания, памяти через занимательные игры математического содержания. презентация к уроку по математике (подготовительная группа) по теме 102
Формулы для вычисления площадей различных треугольников. 10-й класс Формулы для вычисления площадей различных треугольников. 10-й класс 113
Презентация Понятие Отрезок (1 класс) Презентация Понятие Отрезок (1 класс) 124
конспект и презентация урока математики в 3 классе Таблица умножения на 6 (ФГОС) план-конспект урока по математике (3 класс) конспект и презентация урока математики в 3 классе Таблица умножения на 6 (ФГОС) план-конспект урока по математике (3 класс) 129
Ещё раз про проценты Ещё раз про проценты 107
Презентация к родительскому собранию. презентация к уроку (средняя группа) по теме Презентация к родительскому собранию. презентация к уроку (средняя группа) по теме 79
Десятичные дроби Десятичные дроби 117
Функции y=tg x и y=ctg x, их свойства и графики Функции y=tg x и y=ctg x, их свойства и графики 125
Умножение многочленов Умножение многочленов 95
Задачи, приводящие к понятию производной Задачи, приводящие к понятию производной 109
Сложение и вычитание Сложение и вычитание 102
Конус геометрия Конус геометрия 100
Деление двузначного числа на двузначное. Математика. 3 класс. презентация к уроку по математике (3 класс) по теме Деление двузначного числа на двузначное. Математика. 3 класс. презентация к уроку по математике (3 класс) по теме 134
m urok68 m urok68 68
Конспект интегрированной НОД в старшей группе по математике Осень план-конспект занятия по математике (старшая группа) Конспект интегрированной НОД в старшей группе по математике Осень план-конспект занятия по математике (старшая группа) 131
Инструменты, приборы и приспособления для вычислений Инструменты, приборы и приспособления для вычислений 135
Урок математики в 4 классе Диаграммы план-конспект урока по математике (4 класс) Урок математики в 4 классе Диаграммы план-конспект урока по математике (4 класс) 60
Решение планиметрических задач на нахождение геометрических величин Решение планиметрических задач на нахождение геометрических величин 162
Урок – путешествие по математике Сложение и вычитание в пределах 100. Закрепление.(2 класс) Урок – путешествие по математике Сложение и вычитание в пределах 100. Закрепление.(2 класс) 126