Презентация на тему Центральная симметрия

себя, при котором любая точка переходит в симметричную ей

точку, относительно центра О.
Точка О называется центром симметрии фигуры.

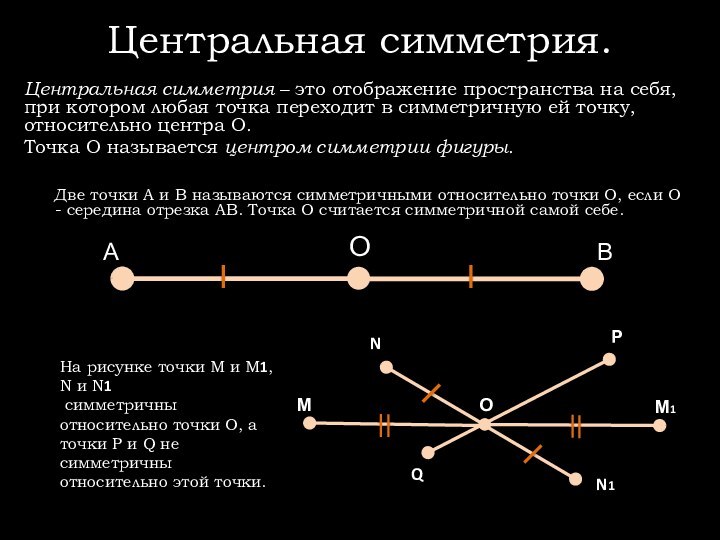
Две точки А и В называются симметричными относительно точки О, если О - середина отрезка АВ. Точка О считается симметричной самой себе.

На рисунке точки М и М1, N и N1
симметричны относительно точки О, а точки Р и Q не симметричны относительно этой точки.

М

М1

N

N1

О

Р

Q

с центром в точке О точки X и Y

отобразились на X' и Y'. Тогда, как ясно из определения центральной симметрии, OX' = -OX, OY' = -OY.

Вместе с тем XY = OY - OX, X'Y' = OY' - OX'

Поэтому имеем: X'Y' = -OY + OX = -XY

Отсюда выходит, что центральная симметрия является движением, изменяющим направление на противоположное и наоборот, движение, изменяющее направление на противоположное, есть центральная симметрия.

Y'

Y

X'

X

O

Свойство центральной симметрии: центральная симметрия переводит прямую (плоскость) в себя или в параллельную ей прямую (плоскость).

Если в прямоугольной системе координат точка А имеет координаты

(x0;y0), то координаты (-x0;-y0) точки А1, симметричной точке А относительно начала координат, выражаются формулами:

x0 = -x0 y0 = -y0

у

х

0

А(x0;y0)

А1(-x0;-y0)

x0

-x0

y0

-y0

окружность и параллелограмм.
Центром симметрии окружности является центр окружности, а

центром симметрии параллелограмма точка пересечения его диагоналей.

Центральная симметрия встречается в форме воздушного и подводного транспорта (воздушный шар, парашют), архитектуре, технике, искусстве и быту.

Центральная симметрия наиболее характерна для плодов растений и некоторых цветов(голубика, черника, вишня, цветок мать-и-мачехи, цветок кувшинки), а также для животных, ведущих подводный образ жизни (амёба).

О

О

симметрии является снежинка.

Центральную симметрию имеют многие геометрические тела. К

ним следует отнести все правильные многогранники (за исключением тетраэдра), все правильные призмы с четным числом боковых граней, некоторые тела вращения (эллипсоид, цилиндр, гиперболоид, тор, шар).

Куб

Октаэдр

Икосаэдр

Додекаэдр

Три различных гиперболоида

BCK, CDP, DAH - правильные
Доказать: KPHM - параллелограмм
Решение:


Рассмотрим центральную

симметрию (поворот на 180 градусов) относительно точки O. Пусть f - центральная симметрия.
f(B) = D, f(A) = C, f(D) = B, f(C) = A.

При центральной симметрии f треугольник BCK (правильный) перейдет в равный ему треугольник DAH (правильный), по свойствам осевой симметрии (углы сохраняются). Аналогично треугольник AMB переходит в треугольник CPD.

f(M) = P, f(K) = H, отсюда KO = OH, MO = OP, по признаку параллелограмма, KPHM – параллелограмм.