- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Центральная симметрия
Содержание
- 2. Центральная симметрияЧто такое центральная симметрия ?Доказательство центральной
- 3. Центральная симметрияОпределение центральной симметрии: поворот на угол
- 4. Доказательство центральной симметрии Проводим отрезки АА’ и
- 5. О симметрии фигурГоворят, что фигура обладает симметрией
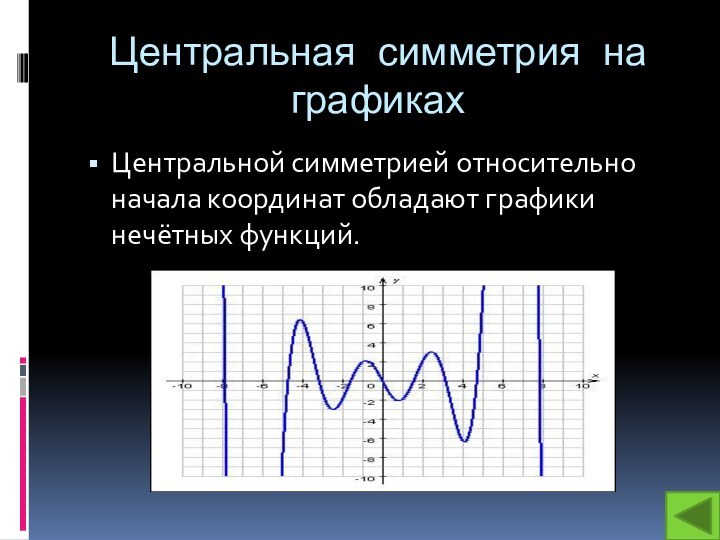
- 6. Центральная симметрия на графиках Центральной симметрией относительно начала координат обладают графики нечётных функций.
- 7. Применение центральной симметрии в жизни Центральная симметрия
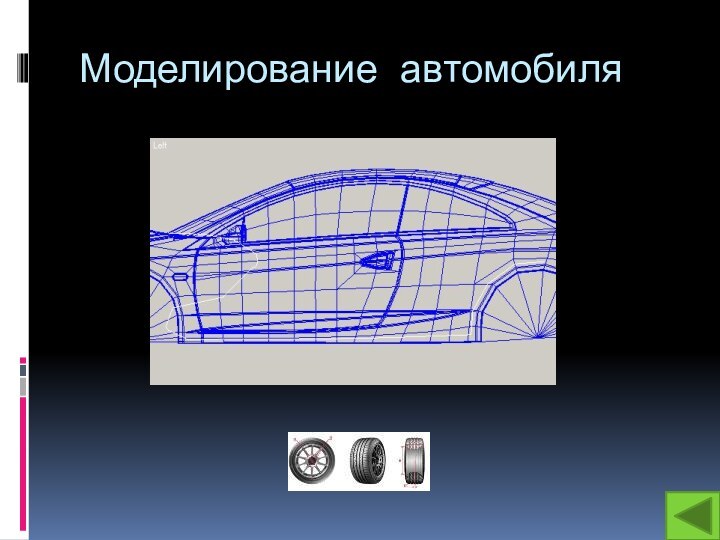
- 8. Моделирование автомобиля
- 9. Архитектура
- 10. Скачать презентацию
- 11. Похожие презентации
Центральная симметрияЧто такое центральная симметрия ?Доказательство центральной симметрииО симметрии фигурЦентральная симметрия на графикахПрименение центральной симметрии в жизни








Слайд 2
Центральная симметрия
Что такое центральная симметрия ?
Доказательство центральной симметрии
О
симметрии фигур
Слайд 3
Центральная симметрия
Определение центральной симметрии: поворот на угол 180
градусов называется центральной симметрией.
Еще можно дать такое определение
Центральная симметрия с центром в точке O это такое отображение плоскости, при котором любой точке X сопоставляется такая точка X', что точка O является серединой отрезка XX'.
Слайд 4
Доказательство центральной симметрии
Проводим отрезки АА’ и ВВ’, они
проходят через т.О
Измеряем и убеждаемся, что АС=AC’, АВ=АВ’,
Порядок
построения точки, центрально симметричной точке В на бумаге:1.Проводим луч ВА.
2.Откладываем на нем от т А в другую сторону отрезок АВ’
Слайд 5
О симметрии фигур
Говорят, что фигура обладает симметрией (симметрична)
, если существует такое движение (не тождественное), переводящее эту
фигуру в себя. Например, фигура обладает поворотной симметрией , если она переходит в себя некоторым поворотом.Рассмотрим симметрию некоторых фигур:
1. Отрезок имеет две оси симметрии (серединный перпендикуляр и прямая, содержащая этот отрезок) и центр симметрии (середина).
2. Треугольник общего вида не имеет осей или центров симметрии, он несимметричен. Равнобедренный (но не равносторонний) треугольник имеет одну ось симметрии: серединный перпендикуляр к основанию.
3. Равносторонний треугольник имеет три оси симметрии (серединные перпендикуляры к сторонам) и поворотную симметрию относительно центра с углом поворота 120 ° .
4.У любого правильного n-угольника есть n осей симметрии, все они проходят через его центр. Он также имеет поворотную симметрию относительно центра с углом поворота
При четном n одни оси симметрии проходят через противоположные вершины, другие - через середины противоположных сторон.
При нечетном n каждая ось проходит через вершину и середину противополжной стороны.
Центр правильного многоугольника с четным числом сторон является его центром симметрии. У правильного многоугольника с нечетным числом сторон центра симметрии нет.
Любая прямая, проходящая через центр окружности является ее осью симметрии, окружность также обладает поворотной симметрией, причем угол поворота может быть любым.