- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Делимость натуральных чисел
Содержание
- 2. Лекция №1Натуральные числа. Делимость натуральных чисел. Действительные числаи действия над ними.
- 3. 1. Классификация действительных чисел.Действительные числа RРациональные
- 4. 2. Натуральные числа. Делимость натуральных чисел.. Определение.Натуральные
- 5. 3. Признаки делимости натуральных чиселНатуральное число n
- 6. 3. Признаки делимости натуральных чиселПример:2: 264; 378605:
- 7. 4. Взаимно простые числа.
- 8. 5. НОК и НОД натуральных чисел.Определение.Наименьшее общее
- 9. 6. Основная теорема арифметики.Представленное в теореме разложение числа называется каноническим разложением числа n.
- 10. 7. Делимость суммы и произведения.
- 11. 8. Свойства, связанные с последовательным расположением натуральных
- 12. 9. Целые числа.Определение.Целые числа – натуральные числа,
- 13. 10. Дробные числа.
- 14. 10. Дробные числа.
- 15. Скачать презентацию
- 16. Похожие презентации
Лекция №1Натуральные числа. Делимость натуральных чисел. Действительные числаи действия над ними.














Слайд 2
Лекция №1
Натуральные числа.
Делимость натуральных чисел.
Действительные числа
и
действия над ними.
Слайд 3
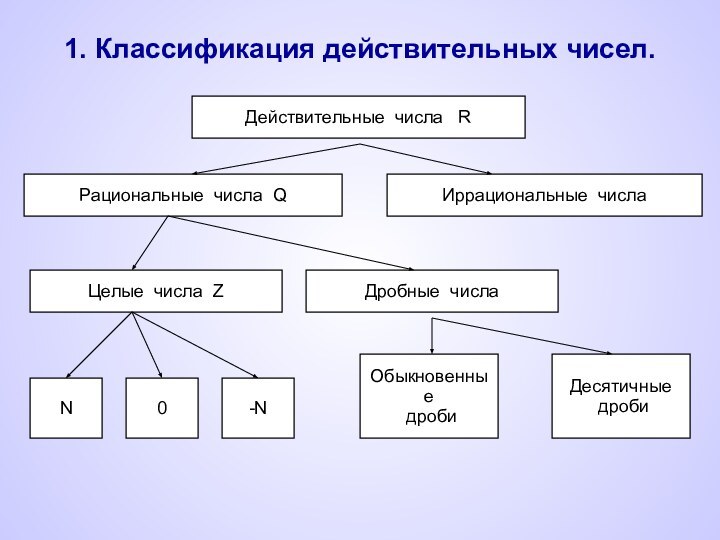
1. Классификация действительных чисел.
Действительные числа R
Рациональные числа
Q
Иррациональные числа
Дробные числа
Целые числа
Z Обыкновенные
дроби
Десятичные
дроби
N
0
-N
Слайд 4
2. Натуральные числа. Делимость натуральных чисел.
.
Определение.
Натуральные числа-
числа, используемые при счете предметов: 1, 2, 3, 4,
…Теорема.
Для любого натурального числа а и натурального числа b существует единственная пара чисел q и r таких, что a=bq+r, где q- натуральное число, r-натуральное число или нуль, причем .
Если остаток r=0, то число а делится на число b нацело (без остатка).
Пример:
Определение.
Натуральные числа- числа, используемые при счете предметов: 1, 2, 3, 4, …
Теорема.
Для любого натурального числа а и натурального числа b существует единственная пара чисел q и r таких, что a=bq+r, где q- натуральное число, r-натуральное число или нуль, причем .
Если остаток r=0, то число а делится на число b нацело (без остатка).
Пример:
Слайд 5
3. Признаки делимости натуральных чисел
Натуральное число n делится
на натуральное число р, равное
1) 2, если его последняя
цифра четная или 0;2) 5, если его последняя цифра 5 или 0;
3) 10, если его последняя цифра 0;
4) 4 (25) , если две его последние цифры нули или образуют число, делящаяся на 4(25);
5) 8 (125) , если три его последние цифры нули или образуют число, делящаяся на 8 (125);
6) 3 (9), если сумма всех его цифр делится на 3 (9);
7) 7 (11, 13), если разность между суммой его цифр стоящих на четных местах и суммой цифр, стоящих на нечетных местах делится на 7 (11,13).
Слайд 6
3. Признаки делимости натуральных чисел
Пример:
2: 264; 37860
5: 379800;
4675
10: 3786300
4 (25): 4500; 5316; 254750
8 (125): 53064 45250
2745;
3663872;
Слайд 8
5. НОК и НОД натуральных чисел.
Определение.
Наименьшее общее кратное
(НОК) натуральных чисел n1,n2,…nk – наименьшее число n, которое
делится нацело на числа n1,n2,…nk.n=НОК(n1,n2,…nk)
Определение.
Наибольший общий делитель (НОД) натуральных чисел n1,n2,…nk – наибольшее число n, на которое делятся нацело числа n1,n2,…nk.
n=НОД(n1,n2,…nk)
Слайд 9
6. Основная теорема арифметики.
Представленное в теореме разложение числа
называется каноническим разложением числа n.
Слайд 11
8. Свойства, связанные с последовательным расположением натуральных чисел.
Одно
из n последовательных целых чисел делится на n;
2) Одно
из двух последовательных четных чисел делится на 4;3) Произведение трех последовательных целых чисел делится
на 6;
4) Произведение двух последовательных четных чисел делится
на 8.