- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему УПРОЩЕНИЕ ВЫРАЖЕНИЙ (5 КЛАСС)
Содержание
- 2. Математику нельзя изучать, наблюдая, как это делает сосед. А. Нивен
- 3. Свойства сложения, вычитания, умножения и деления полезны
- 4. Вычислим сумму: 52 + 287 +
- 6. Также для упрощения вычисления произведений
- 7. Сочетательные (а·в)·с = а·(в·с)и переместительные а ·в
- 8. Распределительный закон умножениячасто применяется для упрощениявычислений.
- 9. Применяя распределительное свойство умноженияотносительно сложения или вычитания
- 10. ЗАПОМНИТЕ!!!Если перед буквой не записано число, топодразумевается,
- 11. Примеры вынесения общего множителя заскобки.73 • 8
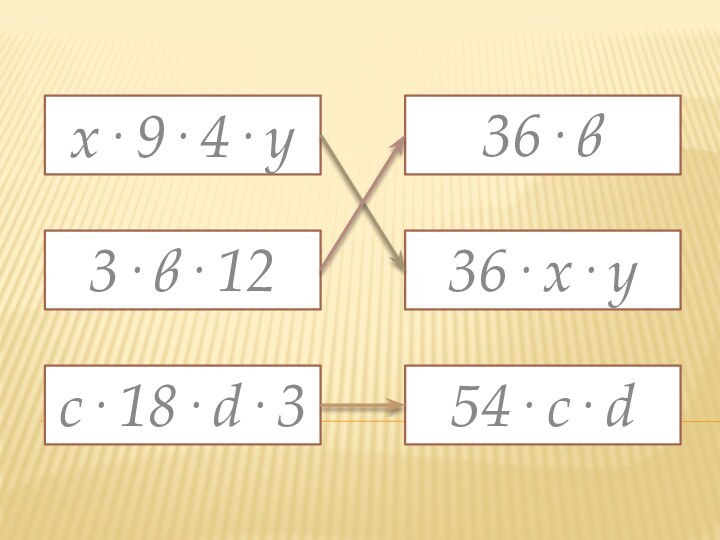
- 12. Упростить выражения
- 13. х· 9· 4· у3· в· 12с· 18· d· 336· в36· х· у54· с· d
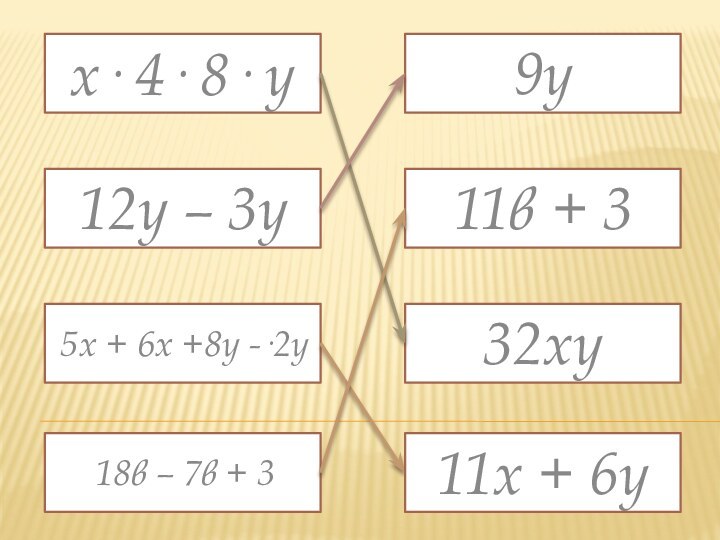
- 14. х· 4· 8· у12y – 3y5x +
- 15. Скачать презентацию
- 16. Похожие презентации
Математику нельзя изучать, наблюдая, как это делает сосед. А. Нивен











Слайд 3 Свойства сложения, вычитания, умножения и деления полезны тем,
что позволяют преобразовывать суммы и
произведения в удобные выражения
для вычислений.
Научимся, как можно с помощью этих свойств упрощать выражения.
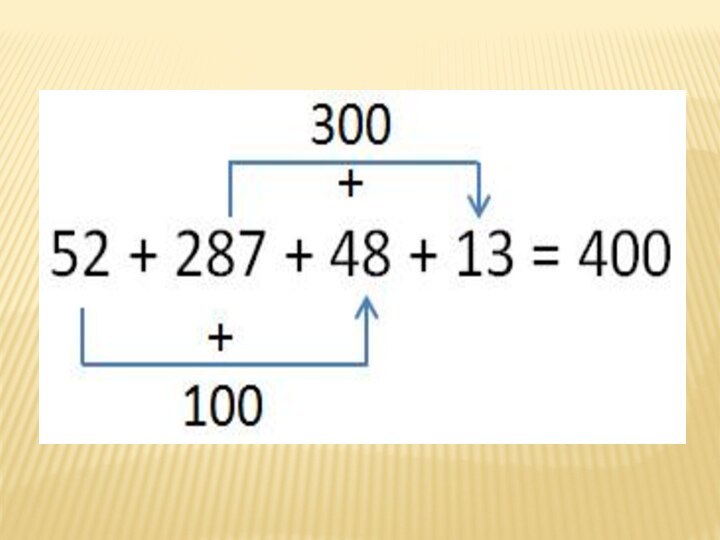
Слайд 4 Вычислим сумму: 52 + 287 + 48 + 13
=
В этом выражении есть числа, при сложении
которых получаются "круглые" числа. Заметив это, легко провести вычисления устно. Воспользуемся переместительным законом сложения: а + в = в + а
Слайд 6 Также для упрощения вычисления произведений можно
использовать переместительный закон умножения:
а ·в = в · а
7
• 2 • 9 • 5 = (2 • 5) • (7 • 9) = 10 • 63 = 630
Слайд 7
Сочетательные (а·в)·с = а·(в·с)
и переместительные а ·в =
в · а
свойства умножения используются и при
упрощении буквенных
выражений: 6 • a • 2 = 6 • 2 • a = 12a
2 • a • 4 • b = 2 • 4 • a • b = 8ab
5b + 8b = (5 + 8) • b = 13b
14y - 12y = (14 - 12) • y = 2y
Слайд 9
Применяя распределительное свойство умножения
относительно сложения или вычитания к
выражению
(a+ b) • с и (a - b)
• c, мы получаем выражение, несодержащее скобки. В этом случае говорят, что мы
раскрыли (опустили) скобки. Для применения свойств
не имеет значения, где записан множитель "c" – перед
скобками или после.
Раскроем скобки в выражениях:
2(t + 8) = 2t + 16
(3b - 5)4 = 4 • 3b - 4 • 5 = 12b - 20
Слайд 10
ЗАПОМНИТЕ!!!
Если перед буквой не записано число, то
подразумевается, что
перед буквой стоит числовой
множитель 1.
t + 4t = (1
+ 4)t = 5tВынесение общего множителя за скобки
Поменяем местами правую и левую часть равенства:
(a + b)с = ac + bc
Получим:
ac + bc = (a + b)с
В таких случаях говорят, что из "ac + bc" вынесен общий
множитель "с" за скобки.
Слайд 11
Примеры вынесения общего множителя за
скобки.
73 • 8 +
7 • 8 = (73 + 7) • 8
= 80 • 8 = 6407x - x - 6 = (7 - 1)x - 6 = 6x - 6 = 6(x - 1)