его начала и конца?
Как находят координаты середины отрезка?
Как находят
длину вектора?Как находят расстояние между точками?
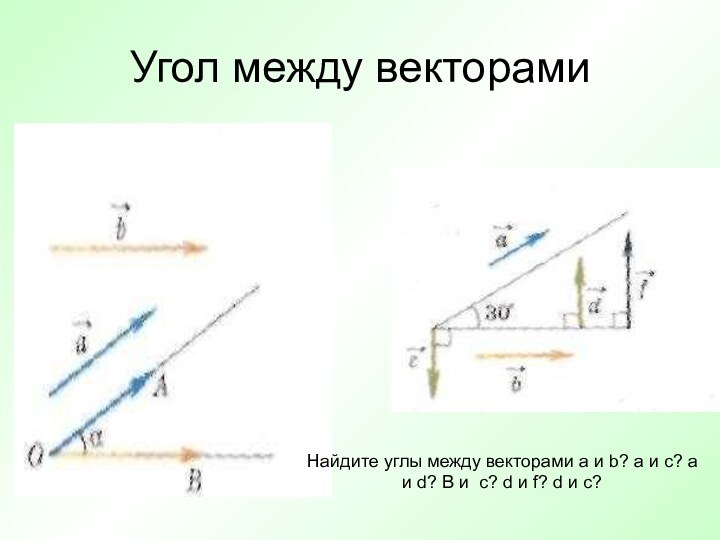
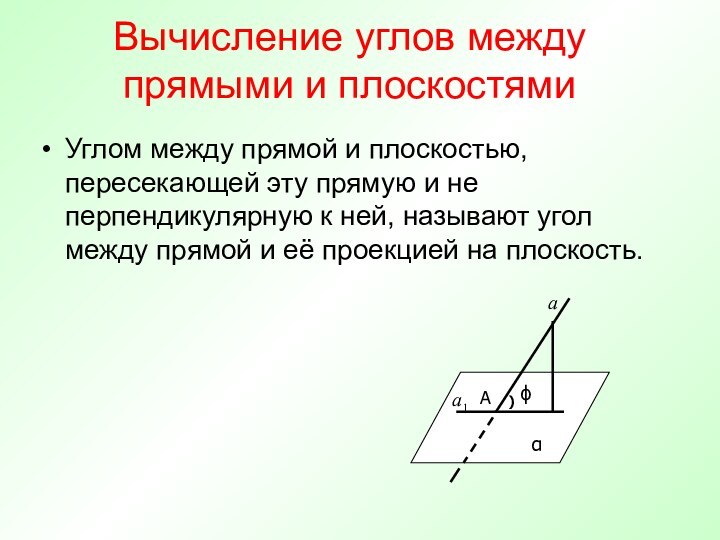
Как вы понимаете выражение «угол между векторами»?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть










Как находят расстояние между точками?
Как вы понимаете выражение «угол между векторами»?
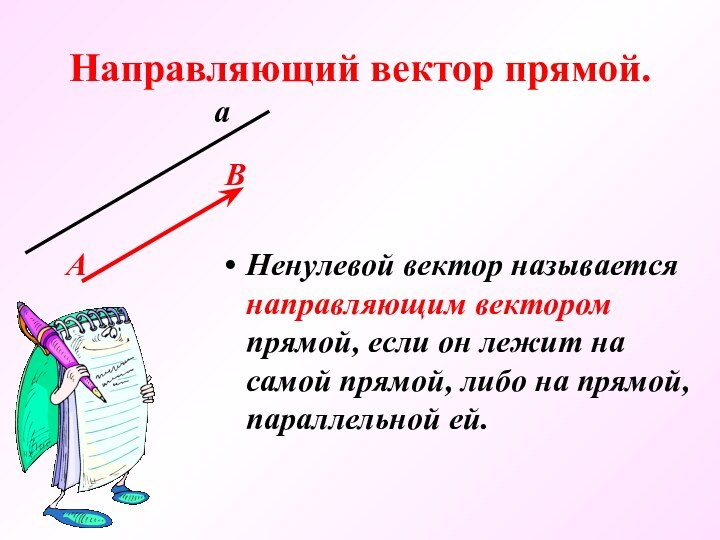
а
В
А
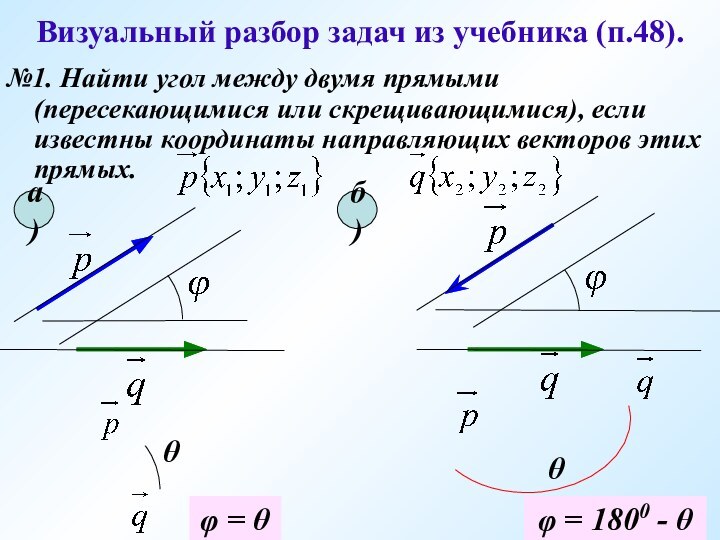
а)
б)
θ
θ
φ = θ
φ = 1800 - θ
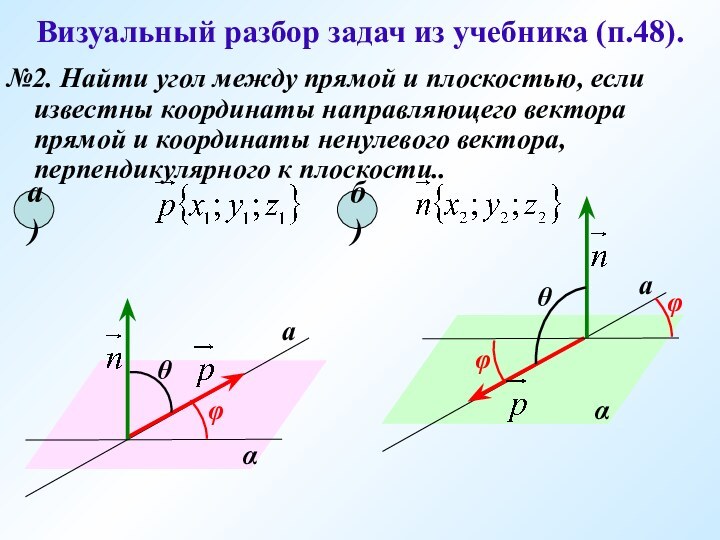
а)
б)
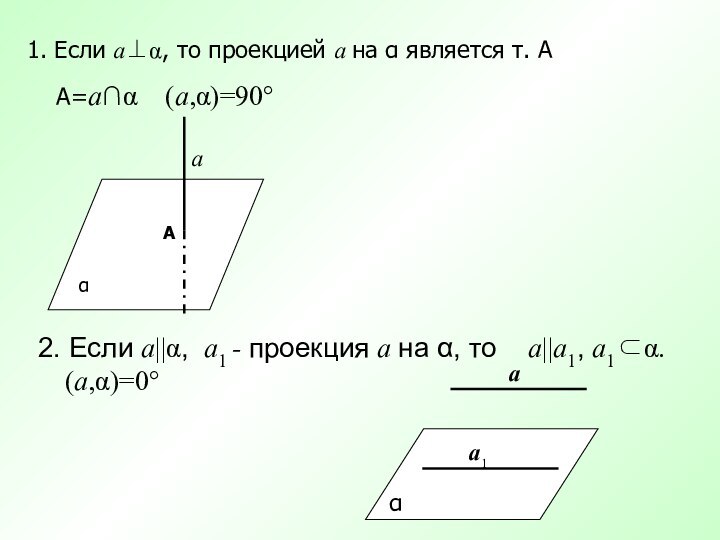
α
а
φ
θ
α
а
φ
φ
θ
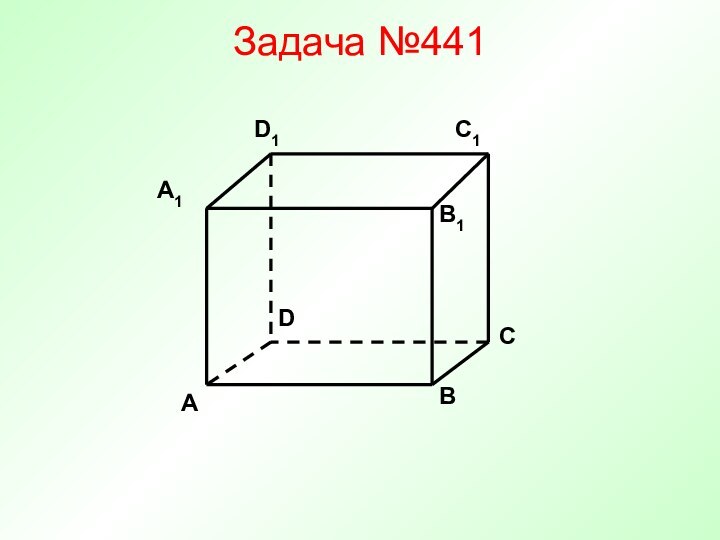
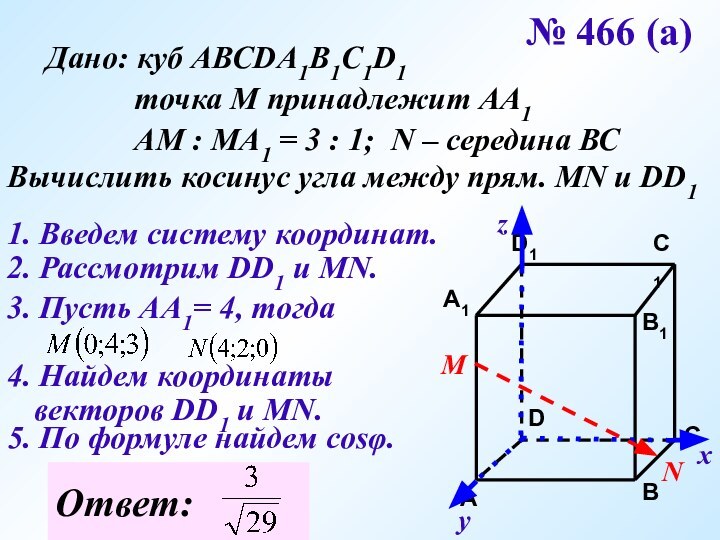
Вычислить косинус угла между прям. MN и DD1
1. Введем систему координат.
х
у
z
2. Рассмотрим DD1 и МN.
М
N
3. Пусть АА1= 4, тогда
4. Найдем координаты векторов DD1 и MN.
5. По формуле найдем cosφ.
Ответ:
х
у
z
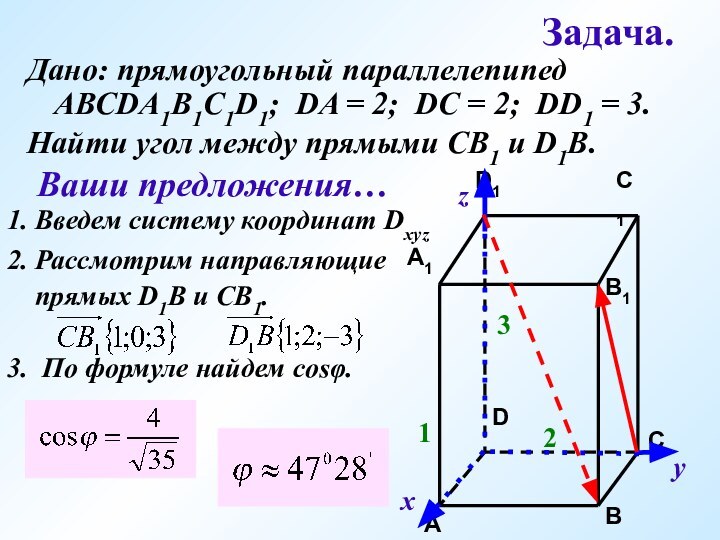
Ваши предложения…
1. Введем систему координат Dxyz
2. Рассмотрим направляющие
прямых D1B и CB1.
3. По формуле найдем cosφ.
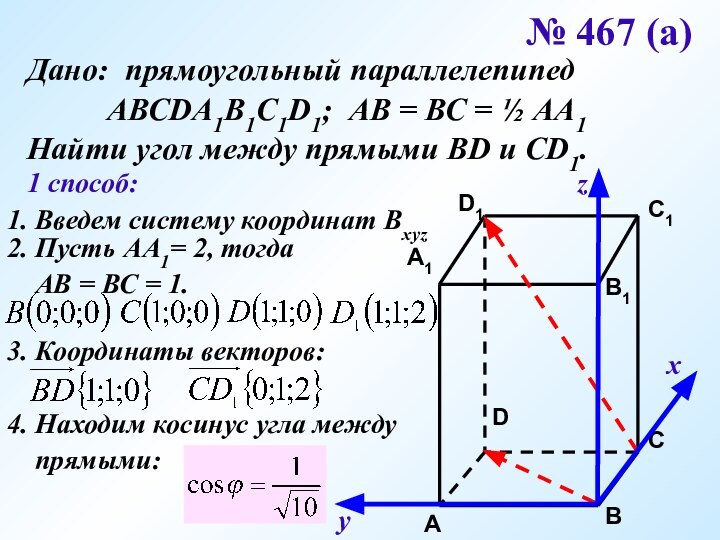
Найти угол между прямыми ВD и CD1.
1 способ:
1. Введем систему координат Bxyz
х
у
z
2. Пусть АА1= 2, тогда
АВ = ВС = 1.
3. Координаты векторов:
4. Находим косинус угла между
прямыми:
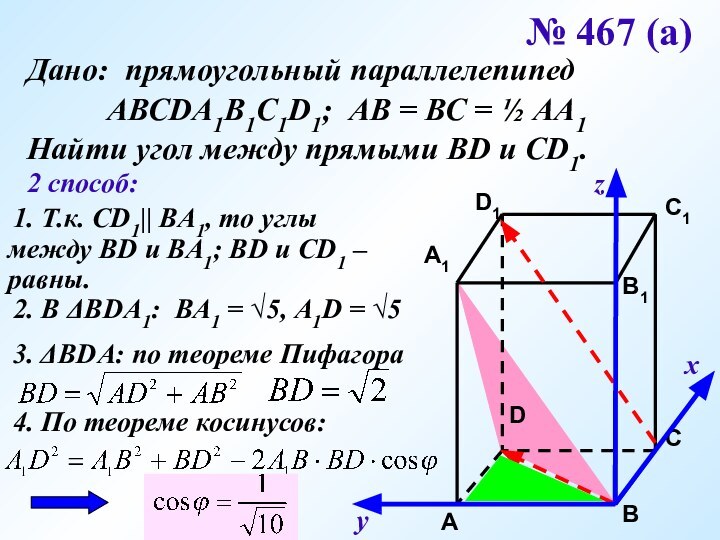
Найти угол между прямыми ВD и CD1.
2 способ:
1. Т.к. СD1|| ВА1, то углы между ВD и ВА1; ВD и СD1 – равны.
2. В ΔВDА1: ВА1 = √5, А1D = √5
3. ΔВDА: по теореме Пифагора
4. По теореме косинусов: