- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Векторы (8 класс)
Содержание
- 2. Историческая справкаТермин вектор (от лат. Vector –
- 3. Что такое вектор?
- 4. Геометрическое понятие вектораНаиболее наглядно величину и направление
- 5. Нулевой векторЛюбую точку плоскости можно считать вектором.
- 6. Длина вектораРасстояние между началом и концом вектора
- 7. Коллинеарные векторыНенулевые векторы называются коллинеарными, если они
- 8. Направление векторовЕсли два ненулевых вектора коллинеарны и
- 9. Направление векторовЕсли два ненулевых вектора коллинеарны и
- 10. Направление векторовЕсли два ненулевых вектора коллинеарны и
- 11. Равенство векторовВекторы называются равными, если они сонаправлены
- 12. Откладывание вектора от данной точкиОт любой точки
- 16. Скачать презентацию
- 17. Похожие презентации
Историческая справкаТермин вектор (от лат. Vector – “ несущий “) впервые появился в 1845 г. у ирландского математика Уильяма Гамильтона (1805 – 1865) в работах по построению числовых систем.








Слайд 3
Что такое вектор?
Понятие
вектора возникает там, где приходится иметь дело с объектами,
которые характеризуются величиной и направлением: например, скорость, сила, давление. Такие величины называются векторными величинами или векторами.
Слайд 4
Геометрическое понятие вектора
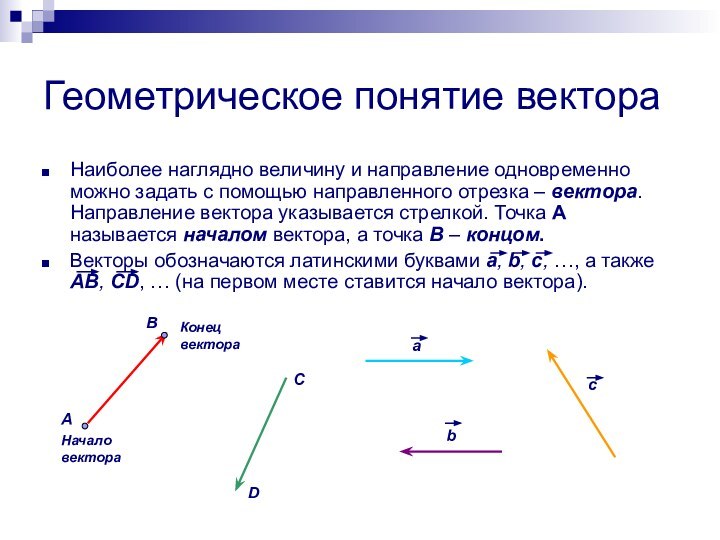
Наиболее наглядно величину и направление одновременно
можно задать с помощью направленного отрезка – вектора. Направление
вектора указывается стрелкой. Точка A называется началом вектора, а точка B – концом.Векторы обозначаются латинскими буквами a, b, c, …, а также AB, CD, … (на первом месте ставится начало вектора).
В
А
Начало вектора
Конец вектора
C
D
a
b
c
Слайд 5
Нулевой вектор
Любую точку плоскости можно считать вектором. Такой
вектор называется нулевым.
Начало нулевого вектора совпадает с его концом.
Нулевой
вектор обозначается 0 или СС.М
С
Слайд 6
Длина вектора
Расстояние между началом и концом вектора называется
длиной или модулем вектора. Длина вектора обозначается |а| или
|АВ|.Длина нулевого вектора считается равной нулю.
a
C
D
N
|AB| = 6 |CD| = 5
|a| = 5 |NN| = 0
(каждая клетка на рисунке имеет сторону, равную единице измерения отрезков)
Слайд 7
Коллинеарные векторы
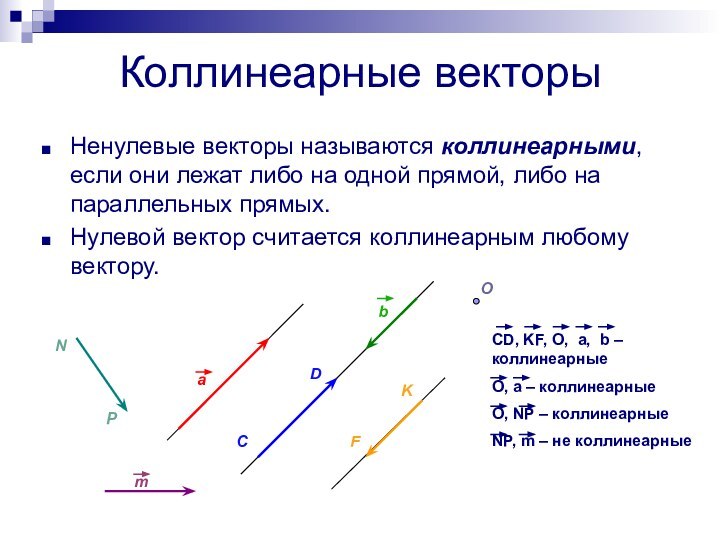
Ненулевые векторы называются коллинеарными, если они лежат
либо на одной прямой, либо на параллельных прямых.
Нулевой вектор
считается коллинеарным любому вектору.CD, KF, O, a, b – коллинеарные
O, a – коллинеарные
O, NP – коллинеарные
NP, m – не коллинеарные
Слайд 8
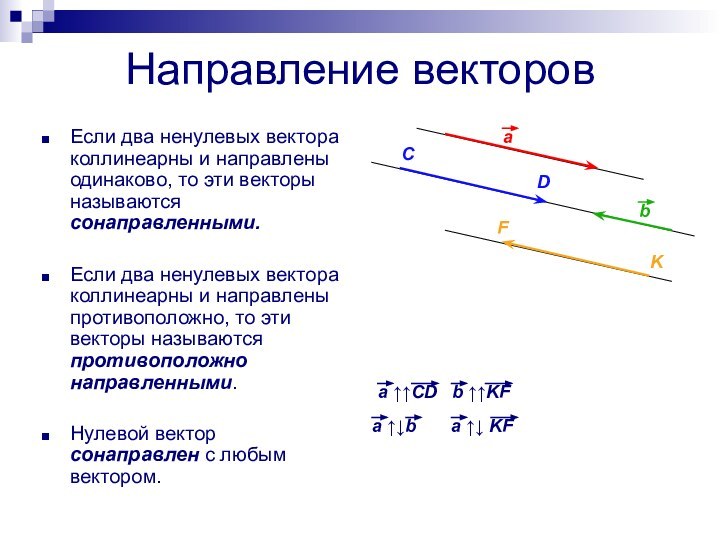
Направление векторов
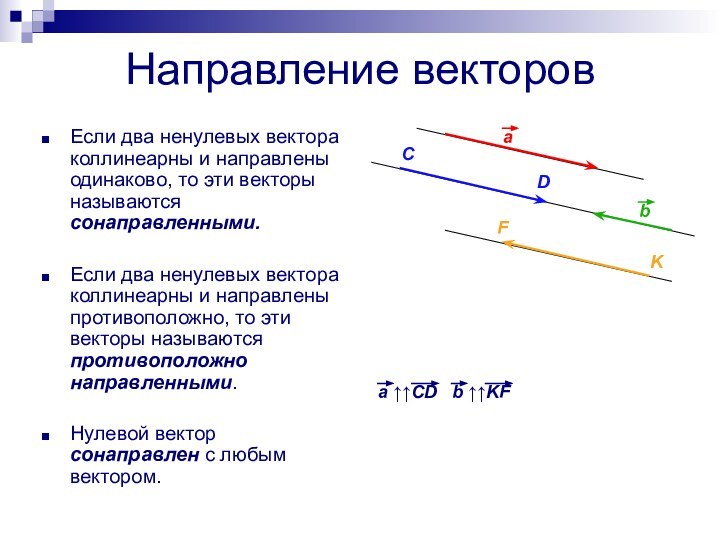
Если два ненулевых вектора коллинеарны и направлены
одинаково, то эти векторы называются сонаправленными.
Если два ненулевых вектора
коллинеарны и направлены противоположно, то эти векторы называются противоположно направленными.Нулевой вектор сонаправлен с любым вектором.
a ↑↑CD b ↑↑KF
Слайд 9
Направление векторов
Если два ненулевых вектора коллинеарны и направлены
одинаково, то эти векторы называются сонаправленными.
Если два ненулевых вектора
коллинеарны и направлены противоположно, то эти векторы называются противоположно направленными.Нулевой вектор сонаправлен с любым вектором.
a ↑↑CD b ↑↑KF
C
D
Слайд 10
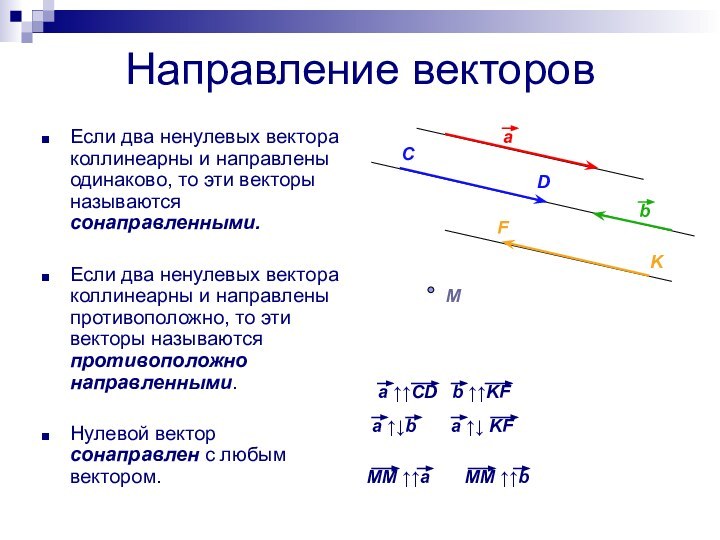
Направление векторов
Если два ненулевых вектора коллинеарны и направлены
одинаково, то эти векторы называются сонаправленными.
Если два ненулевых вектора
коллинеарны и направлены противоположно, то эти векторы называются противоположно направленными.Нулевой вектор сонаправлен с любым вектором.
a ↑↑CD b ↑↑KF
a ↑↓b a ↑↓ KF
a
C
D
Слайд 11
Равенство векторов
Векторы называются равными, если они сонаправлены и
их длины равны.
Равенство векторов обозначается: a = b
Все нулевые
векторы равны друг другу.
Слайд 12
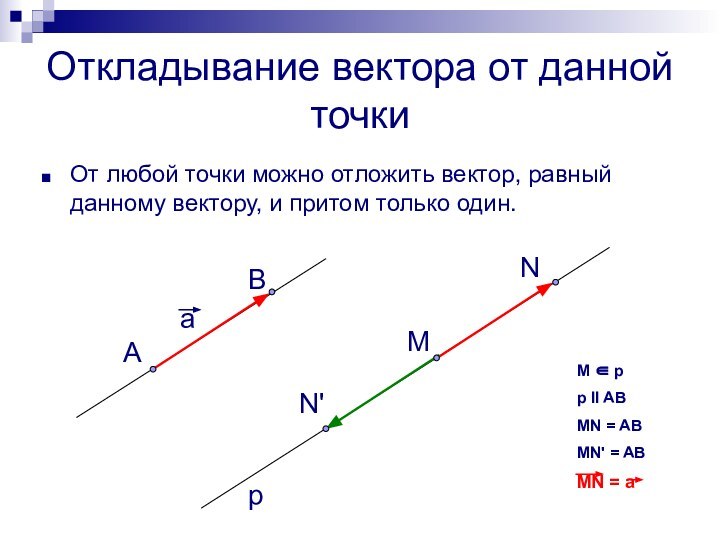
Откладывание вектора от данной точки
От любой точки можно
отложить вектор, равный данному вектору, и притом только один.
а
А
В
М
N'
N
p
M
pp II AB
MN = AB
MN' = AB
MN = a
Слайд 13
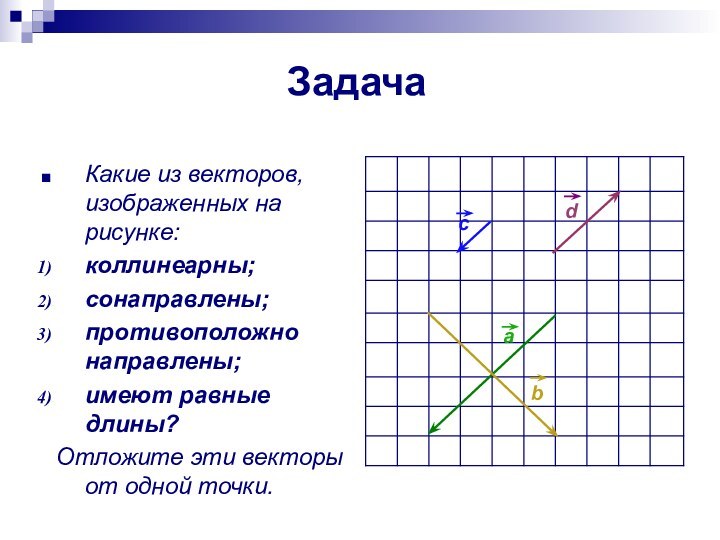
Задача
Какие из векторов, изображенных на рисунке:
коллинеарны;
сонаправлены;
противоположно
направлены;имеют равные длины?
Отложите эти векторы от одной точки.
a
b
d
c
Слайд 14
Задача
На рисунке изображена равнобедренная трапеция KLMN.
а)
Укажите сонаправленные, противоположно направленные, равные вектора.б) Укажите векторы, длины которых равны. Равны ли при этом сами векторы?
K
L
M
N
Слайд 15
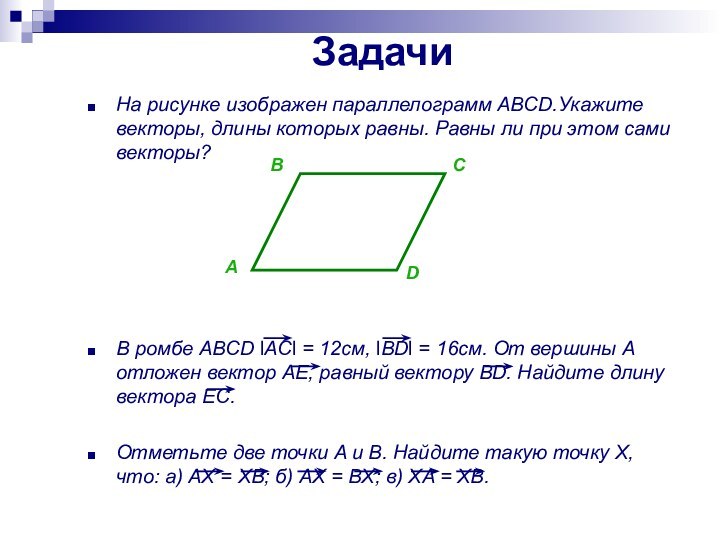
Задачи
Даны вектор BC и точка D(1;-2). Отложите от
точки D вектор, равный вектору BC.Как должен быть расположен ненулевой вектор a относительно прямой k, чтобы нашлись лежащие на этой прямой векторы, равные a? Сколько таких векторов найдется? Отметьте на чертеже три из них.
Векторы AB и DC равны. Докажите, что если точки A, B, C и D не лежат на одной прямой, то четырехугольник ABCD ― параллелограмм.