компьютере;
расширить и систематизировать знания о числе, системах счисления;
сформировать
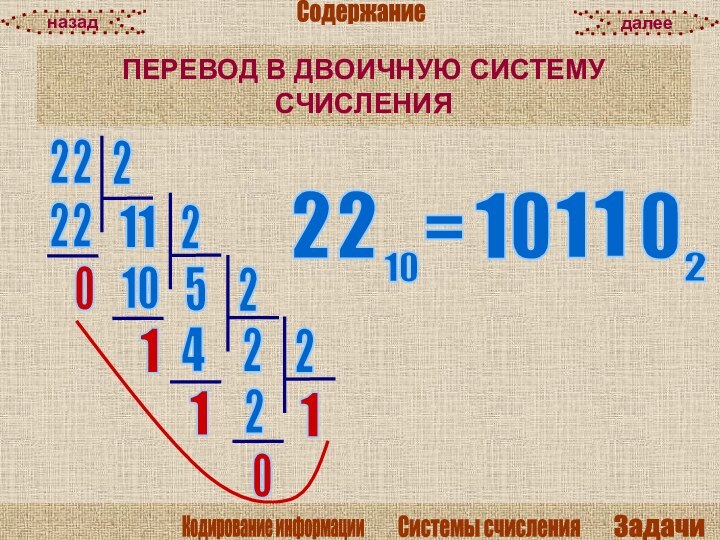
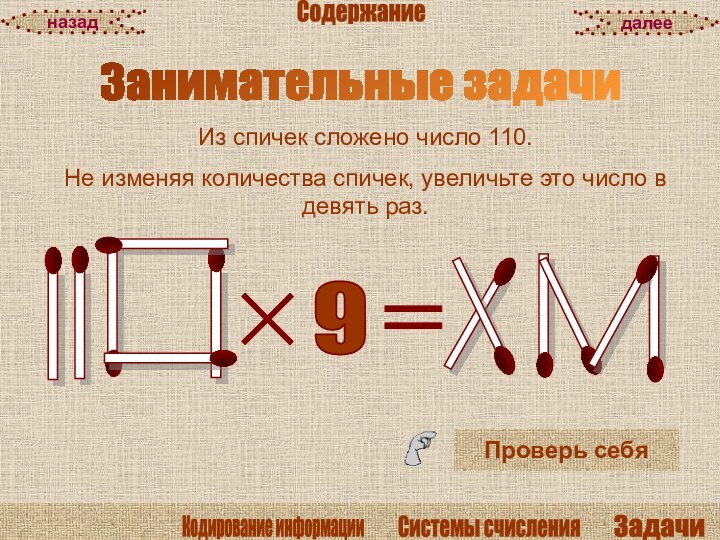
умение решать задачи по переводу числа из одной системы счисления в другую; продолжить формирование ведущих компонентов компьютерной грамотности.