- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Винтовые поверхности
Содержание
- 2. Винтовая поверхность образуется винтовым перемещением линии (образующей).
- 3. В технике часто встречаются винтовые поверхности, образованные
- 4. Прямые и наклонные геликоиды подразделяются на закрытые
- 5. Следует отметить одно важное свойство винтовых поверхностей,
- 6. Тело ограниченное цилиндрическим и винтовыми поверхностями называют
- 7. Развертки поверхности
- 8. Разверткой называется плоская фигура, полученная при совмещении
- 9. ОСНОВНЫЕ СВОЙСТВА РАЗВЕРТКИ 1) Длины двух соответствующих линий поверхности
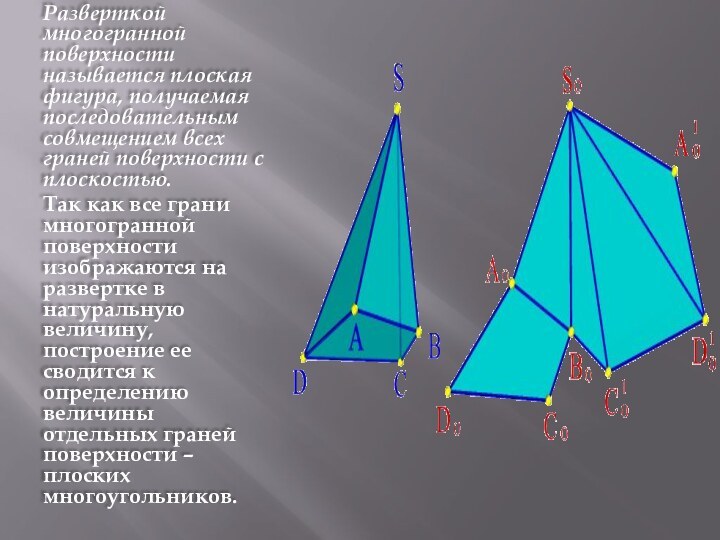
- 10. Разверткой многогранной поверхности называется плоская фигура, получаемая
- 11. При построении развертки пирамида применяется способ треугольника.
- 12. Развертки тел
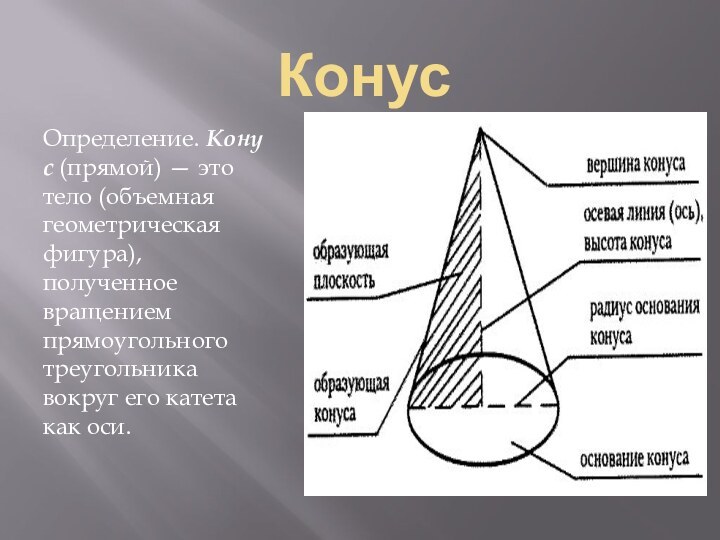
- 13. КонусОпределение. Конус (прямой) — это тело (объемная геометрическая фигура), полученное вращением прямоугольного треугольника вокруг его катета как оси.
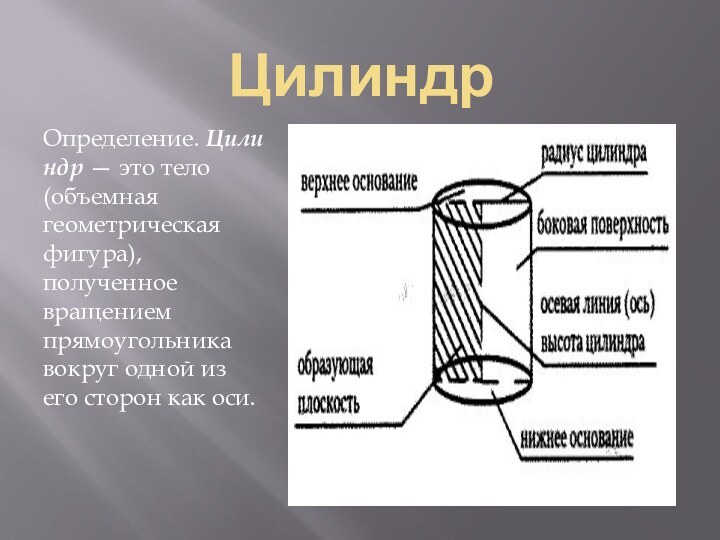
- 14. ЦилиндрОпределение. Цилиндр — это тело (объемная геометрическая фигура), полученное вращением прямоугольника вокруг одной из его сторон как оси.
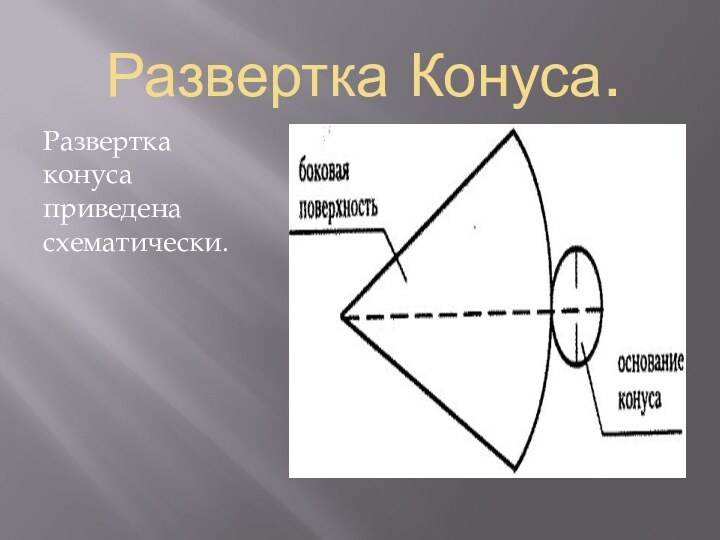
- 15. Развертка Конуса.Развертка конуса приведена схематически.
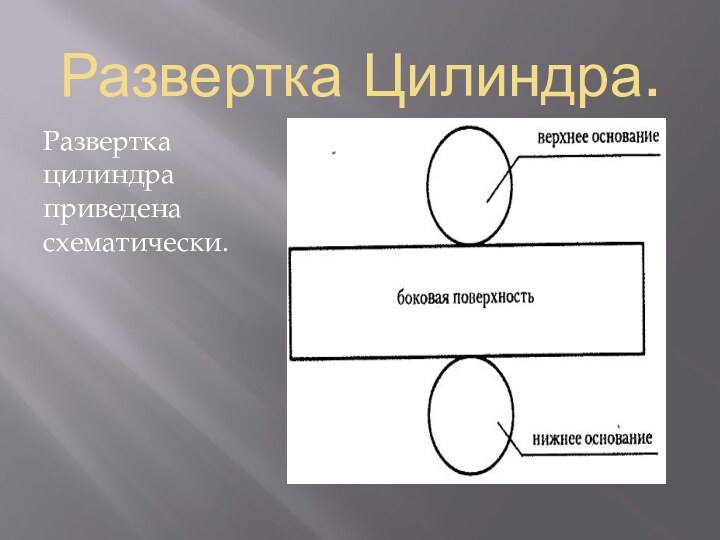
- 16. Развертка Цилиндра.Развертка цилиндра приведена схематически.
- 17. Скачать презентацию
- 18. Похожие презентации
Винтовая поверхность образуется винтовым перемещением линии (образующей). Поверхность можно задать начальным положением образующей и направляющей – цилиндрической винтовой линией, которая называется гелисой.


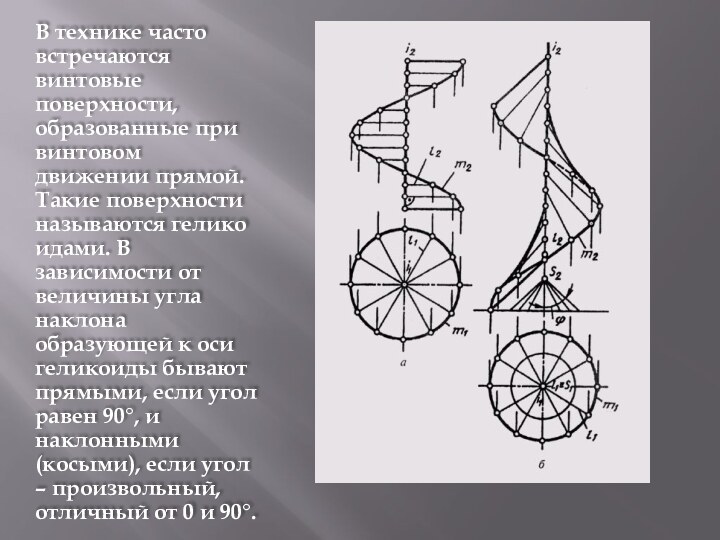








Слайд 3 В технике часто встречаются винтовые поверхности, образованные при
винтовом движении прямой. Такие поверхности называются геликоидами. В зависимости от
величины угла наклона образующей к оси геликоиды бывают прямыми, если угол равен 90°, и наклонными (косыми), если угол – произвольный, отличный от 0 и 90°.Слайд 4 Прямые и наклонные геликоиды подразделяются на закрытые и
открытые. Признаком для такого деления служат взаимное расположение оси
геликоида и образующей. Если образующая и ось пересекаются, геликоид называют закрытым, если скрещиваются – открытым. Выше были рассмотрены закрытые геликоиды.Слайд 5 Следует отметить одно важное свойство винтовых поверхностей, состоящее
в том, что они могут сдвигаться, т.е. совершая винтовое
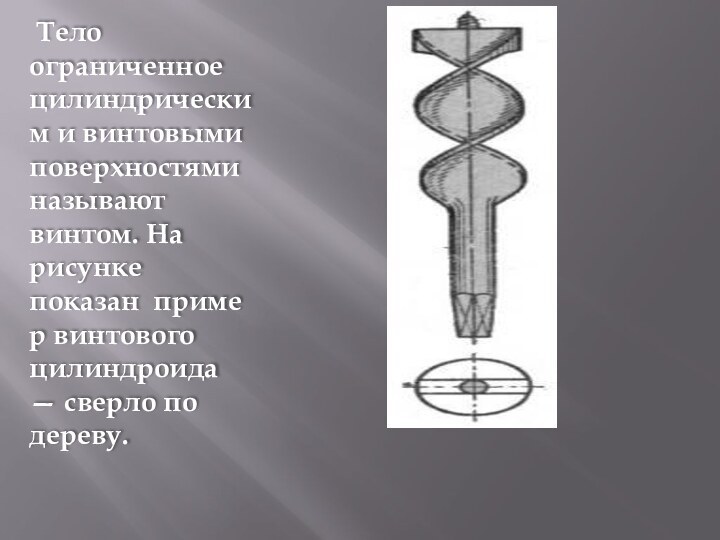
перемещение поверхность скользит вдоль самой себя. Это свойство обеспечивает винтовым поверхностям широкое применение: винты, шнеки, сверла, пружины, поверхности лопаток турбин и вентиляторов, рабочие органы судовых движителей, конструкции винтовых линий и др. Винтовые поверхности, и в частности прямой и наклонный геликоиды, широко применяются в технике. Этими поверхностями ограничены червяки (в червячных передачах) винты, болты и т.п.Слайд 6 Тело ограниченное цилиндрическим и винтовыми поверхностями называют винтом.
На рисунке показан пример винтового цилиндроида — сверло по
дереву.Слайд 8 Разверткой называется плоская фигура, полученная при совмещении поверхности
геометрического тела с одной плоскостью (без наложения граней или
иных элементов поверхности друг на друга).Приступая к изучению развертки поверхности, последнюю целесообразно рассматривать как гибкую, нерастяжимую пленку. Некоторые из представленных таким образом поверхностей можно путем изгибания совместить с плоскостью. При этом, если отсек поверхности может быть совмещен с плоскостью без разрывов и склеивания, то такую поверхность называют развертывающейся, а полученную плоскую фигуру – ее разверткой.
Слайд 9
ОСНОВНЫЕ СВОЙСТВА РАЗВЕРТКИ
1) Длины двух соответствующих линий поверхности и
ее развертки равны между собой;
Угол между линиями на поверхности
равен углу между соответствующими им линиями на развертке;2) Прямой на поверхности соответствует также прямая на развертке;
Параллельным прямым на поверхности соответствуют также параллельные прямые на развертке;
3) Если линии, принадлежащей поверхности и соединяющей две точки поверхности, соответствует прямая на развертке, то эта линия является геодезической.