- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Золотое сечение
Содержание
- 2. «Математика владеет не только истиной, но и
- 3. Тетраэдр, Гексаэдр, Октаэдр, Икосаэдр и Додекаэдр
- 4. Додекаэдр имеет 12 граней, 30 ребер и 60
- 5. Золотое сечение - это универсальное проявление структурной
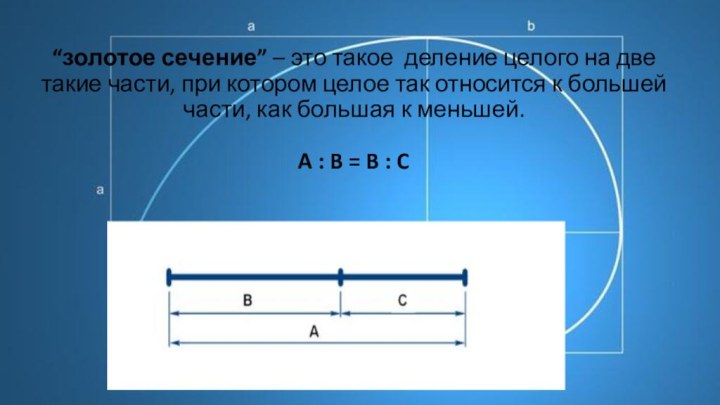
- 6. “золотое сечение” – это такое деление
- 7. Решаем пропорцию A : B = B
- 8. Алгебраические свойства «золотой пропорции»Представим уравнение золотой пропорциих²-х-1=0
- 9. В дошедшей до нас античной литературе деление
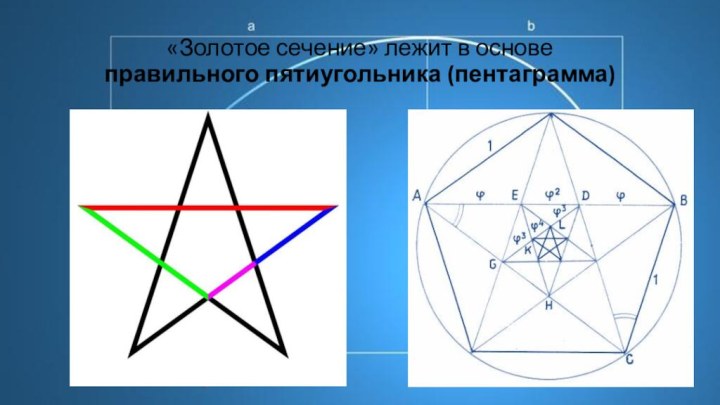
- 10. «Золотое сечение» лежит в основе правильного пятиугольника (пентаграмма)
- 11. Пятиконечная звезда с древних времен символ совершенства,
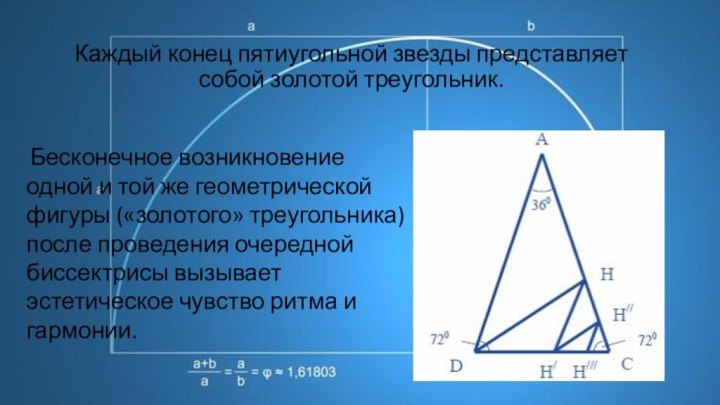
- 12. Каждый конец пятиугольной звезды представляет собой золотой
- 13. Золотое сечение в природеВ живой природе широко
- 14. Каждые восемь лет планета Венера описывает абсолютно
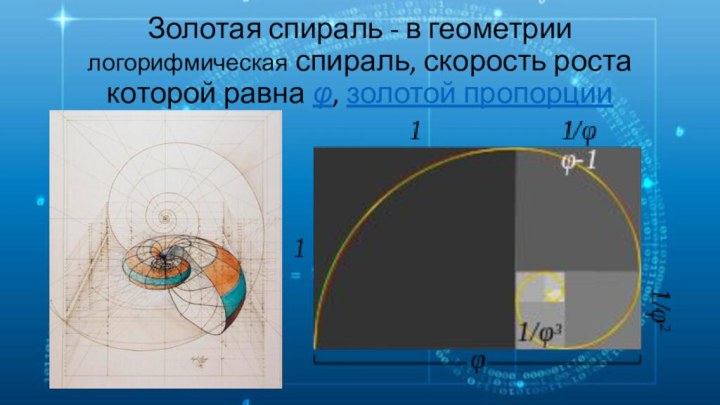
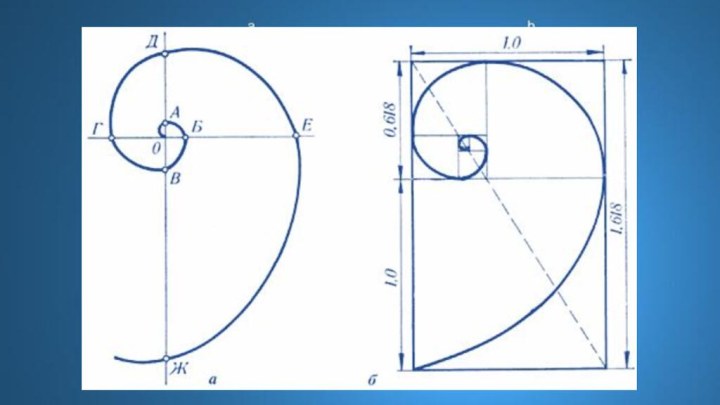
- 15. Золотая спираль - в геометрии логорифмическая спираль, скорость роста которой равна φ, золотой пропорции
- 16. Существует несколько похожих спиралей, которые близки, но не совпадают в точности с золотой спиралью
- 18. Тема золотого сечения популярна в современном образовательном
- 22. Скачать презентацию
- 23. Похожие презентации
«Математика владеет не только истиной, но и высокой красотой – красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства». Бертран Рассел


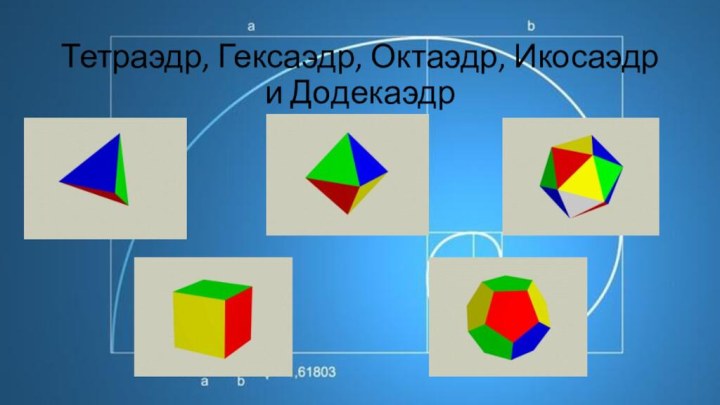














Слайд 4 Додекаэдр имеет 12 граней, 30 ребер и 60 плоских
углов на своей поверхности. Если исходить из гипотезы, что
египтяне знали додекаэдр и его числовые характеристики 12, 30. 60, то каково же было их удивление, когда они обнаружили, что этими же числами выражаются циклы Солнечной системы, а именно, 12-летний цикл Юпитера, 30-летний цикл Сатурна и, наконец, 60-летний цикл Солнечной системы. Таким образом, между такой совершенной пространственной фигурой, как додекаэдр, и Солнечной системой, существует глубокая математическая связь! Такой вывод сделали античные ученые. Это и привело к тому, что додекаэдр был принят в качестве «главной фигуры», которая символизировала Гармонию МирозданияСлайд 5 Золотое сечение - это универсальное проявление структурной гармонии.
Оно встречается в природе, науке, искусстве – во всем,
с чем может соприкоснуться человек.Слайд 6 “золотое сечение” – это такое деление целого на
две такие части, при котором целое так относится к
большей части, как большая к меньшей. A : B = B : CСлайд 7 Решаем пропорцию A : B = B :
C А*С=В² т.к. С=А-В, то получим А²-АВ-В²=0 . Разделив
на В² и обозначив А:B=x мы приходим к следующему алгебраическому уравнению х²-х-1=0 Решением является положительный корень х=(1+√5)/2 ≈ 1,618…Отношение А:В обозначают буквой Ф = 1,62.
Ф – не зависит от длины отрезка и называется числом Фидия.
В процентном округлённом значении золотое сечение — это деление какой-либо величины в отношении 62 % и 38 %.
Слайд 8
Алгебраические свойства «золотой пропорции»
Представим уравнение золотой пропорции
х²-х-1=0
в
следующем виде: х²=х+1.
Если корень Ф (золотая пропорция) подставить вместо
х, то получим следующее замечательное тождество:Ф²=Ф+1.
Если все члены тождества разделить на Ф, то придем к следующему выражению:
Ф=1+1/Ф или Ф-1=1/Ф.
Слайд 9 В дошедшей до нас античной литературе деление отрезка
в крайнем и среднем отношении (ἄκρος καὶ μέ- σος
λόγος) впервые встречается в «Началах» Евклида (ок. 300 лет до н. э.), где оно применяется для построения правильного пятиугольника.Слайд 11 Пятиконечная звезда с древних времен символ совершенства, а
в средние века ее наделяли еще магическими свойствами. Вспомните
«Фауста» Гете (в переводе Н. Холодковского):Мефистофель:
Нет, трудновато выйти мне теперь
Тут кое-что мешает мне немного:
Волшебный знак у вашего порога.
Фауст:
Не пентаграммаль этому виной?
Но как же, бес, пробрался ты за мной?
Каким путем впросак попался?





























