Презентация на тему Вневписанная окружность

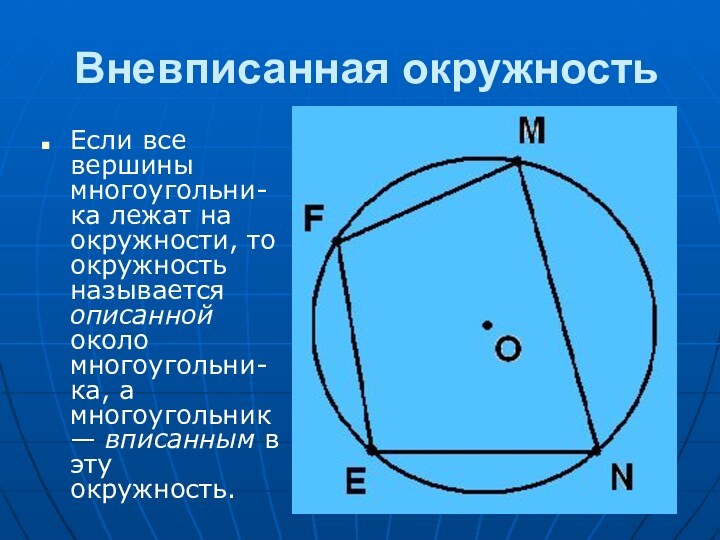
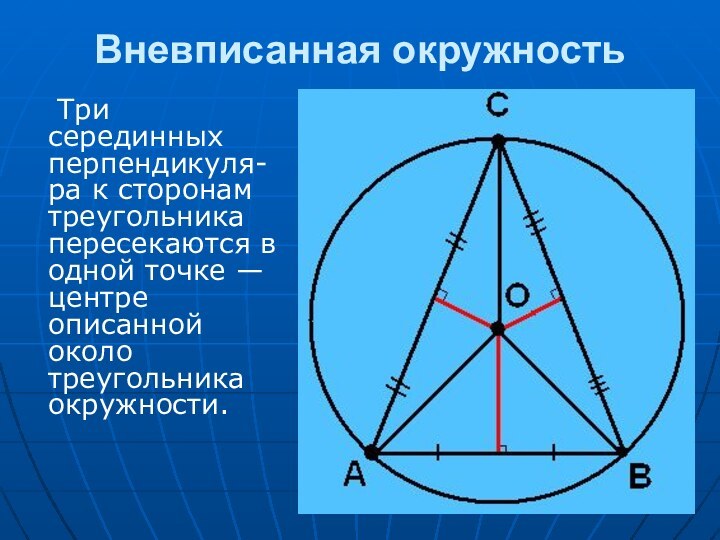
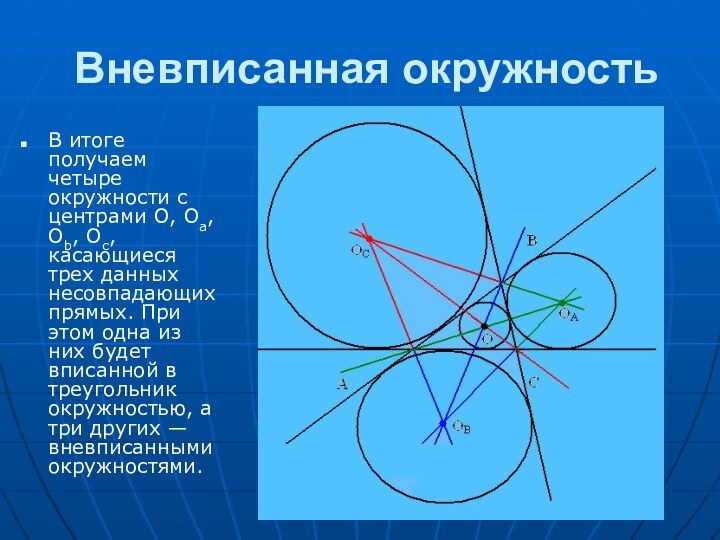
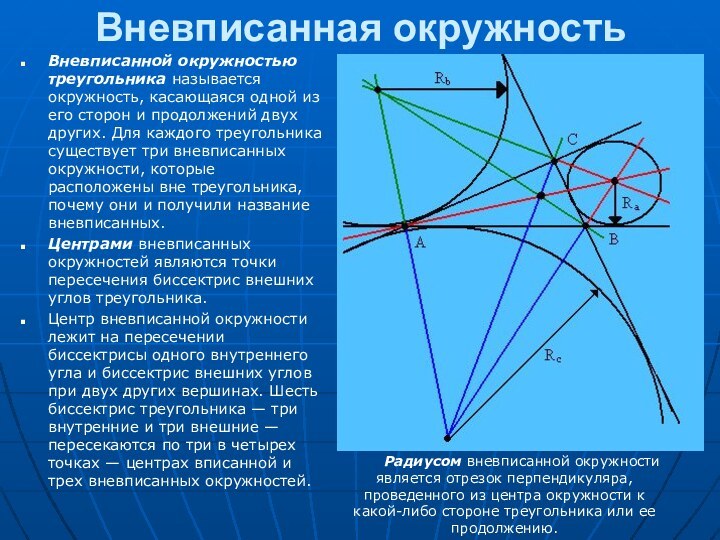
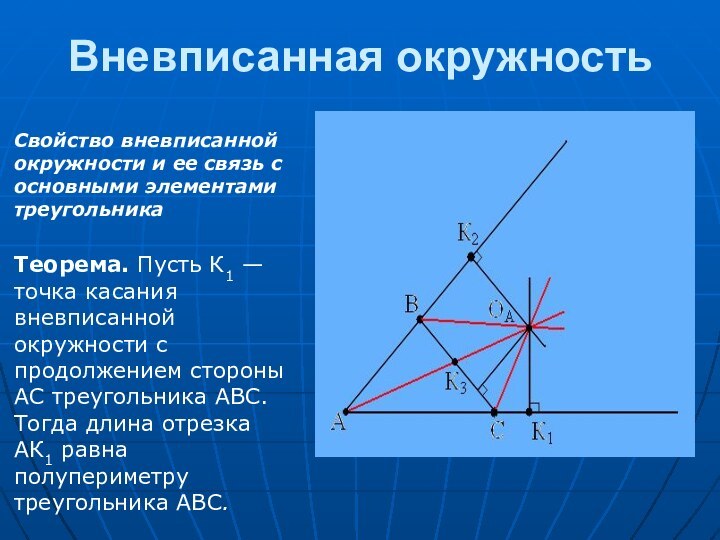
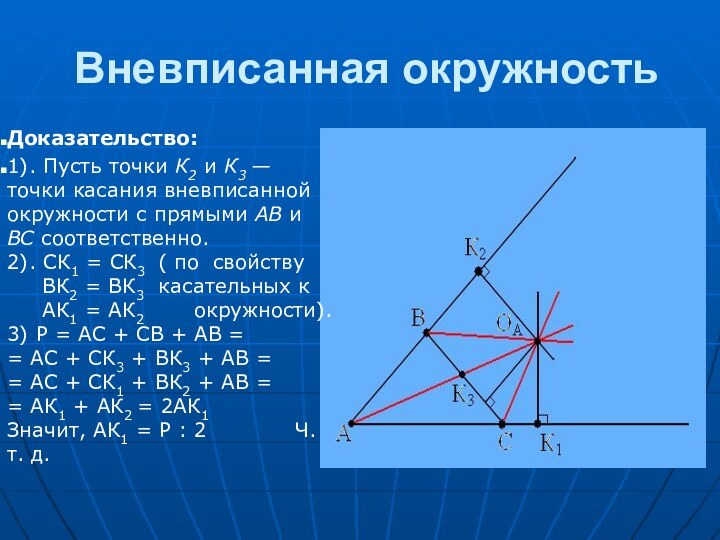
в геометрии особую роль. За несколько тысячелетий геометры столь

подробно изучили треугольник, что иногда говорят о «геометрии треугольника» как о самостоятельном разделе элементарной геометрии.
Первые упоминания о треугольнике и его свойствах можно найти в египетских папирусах, которым более 4000 лет. Через 2000 лет в Древней Греции изучение свойств треугольника достигает высокого уровня — достаточно вспомнить теорему Пифагора и формулу Герона.
Центральное место в геометрии треугольника занимают свойства так называемых замечательных точек и линий.

то окружность называется описанной около многоугольни-ка, а многоугольник —

вписанным в эту окружность.

то окружность называется вписанной в многоугольник, а многоугольник —

описанным около этой окружности.

в одной точке — центре описанной около треугольника окружности.

точке- центре вневписанной в этот треугольник окружности.

Если рассмотреть

дополнительно биссектрисы трех пар внешних углов треугольника, то получаются еще три замечательных точки — центры вневписанных окружностей.

центры окружностей касающихся прямых АВ, ВС, СА.

О, Оа, Ob, Oc, касающиеся трех данных несовпадающих прямых.

При этом одна из них будет вписанной в треугольник окружностью, а три других — вневписанными окружностями.

из его сторон и продолжений двух других. Для каждого

треугольника существует три вневписанных окружности, которые расположены вне треугольника, почему они и получили название вневписанных.
Центрами вневписанных окружностей являются точки пересечения биссектрис внешних углов треугольника.
Центр вневписанной окружности лежит на пересечении биссектрисы одного внутреннего угла и биссектрис внешних углов при двух других вершинах. Шесть биссектрис треугольника — три внутренние и три внешние — пересекаются по три в четырех точках — центрах вписанной и трех вневписанных окружностей.

Радиусом вневписанной окружности является отрезок перпендикуляра, проведенного из центра окружности к какой-либо стороне треугольника или ее продолжению.

основными элементами треугольника

Теорема. Пусть К1 — точка касания вневписанной

окружности с продолжением стороны АС треугольника ABC. Тогда длина отрезка АК1 равна полупериметру треугольника ABC.

— точки касания вневписанной окружности с прямыми АВ и

ВС соответственно.
2). СК1 = СК3 ( по свойству
ВК2 = ВК3 касательных к
АК1 = АК2 окружности).
3) Р = АС + СВ + АВ =
= АС + СК3 + ВК3 + АВ =
= АС + СК1 + ВК2 + АВ =
= АК1 + АК2 = 2АК1
Значит, АК1 = Р : 2 Ч. т. д.

треугольник окружности с центрами вневписанных окружностей, делятся пополам окружностью,

описанной вокруг этого треугольника