числа точек, называемых вершинами графа, и попарно соединяющих некоторые
из этих вершин линий, называемых ребрами или дугами графа.Граф
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть









![Элементы теории графов. Способы обходов графов Program graf;Var n,v,u: integer; gr: array [1..30, 1..30] of integer; nov: array [1..15] of](/img/tmb/14/1365107/f4619b2818f50d7898b0547b24c6e391-720x.jpg)
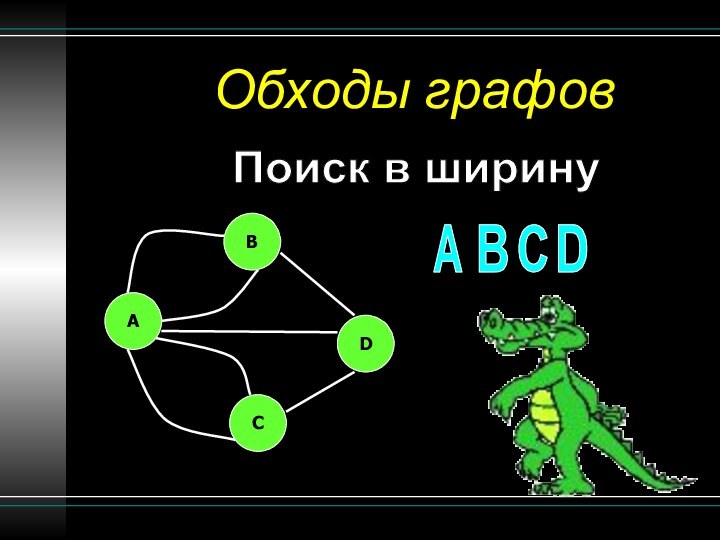

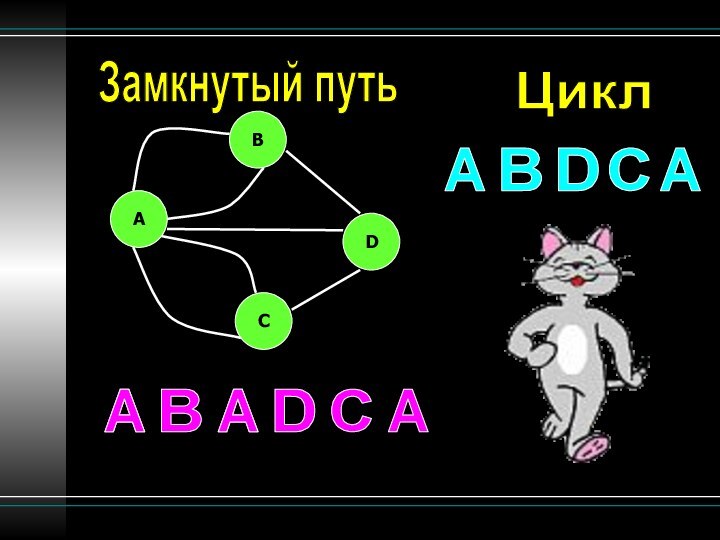
Граф
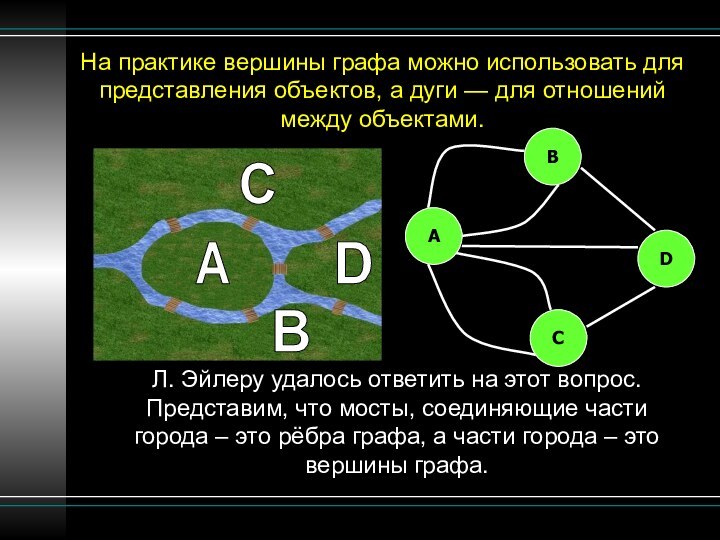
Кёненсбергские мосты
A
A
C
B
D
Кёненсбергские мосты
B
A
C
D
Begin
n:=4;
for v:=1 to n do
begin
nov [v]:= true;
Writeln;
For u:=1 to n do begin nov [u]:=true;
Write (‘ gr [‘ ,v,u, ‘ ]=‘);
Read (gr [v,u]);
Размерность массива
n =4
End;
End;
For v:=1 to n do begin
IF nov [v] then dfs (v);
End;
Readln;
End.