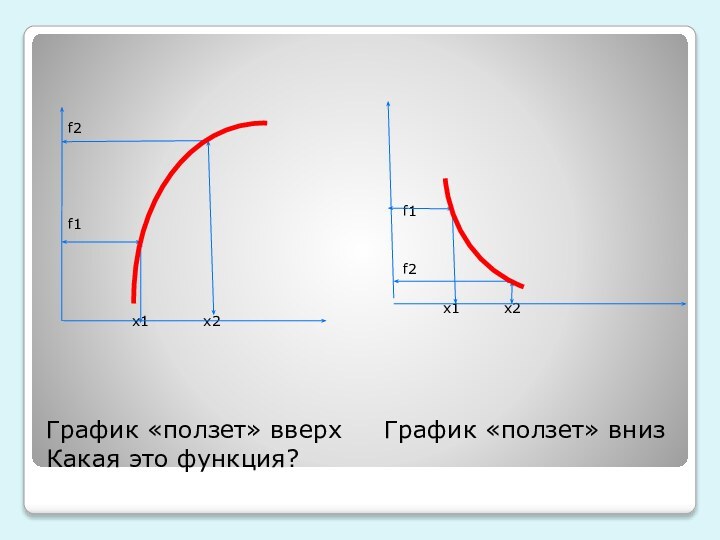
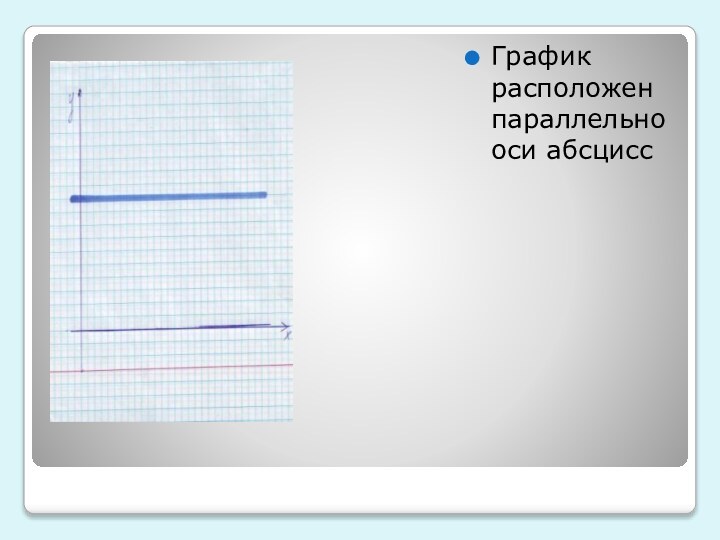
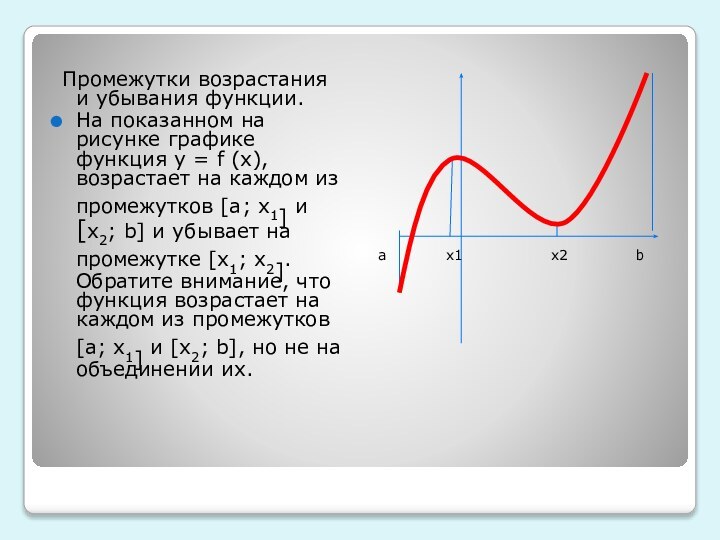
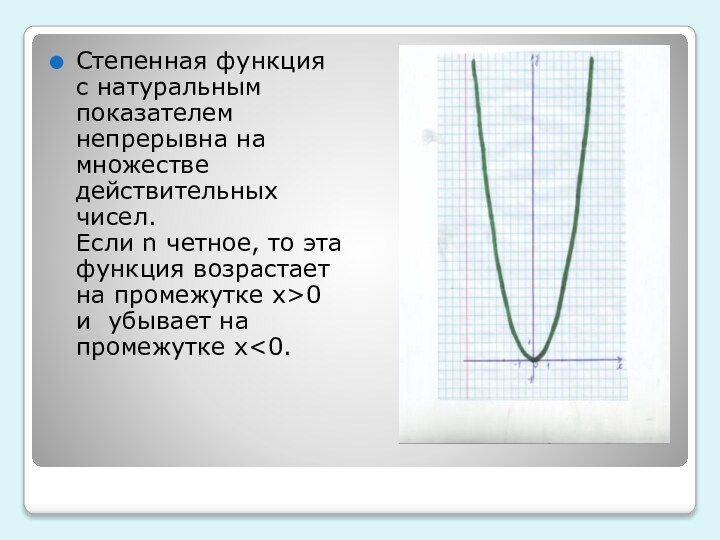
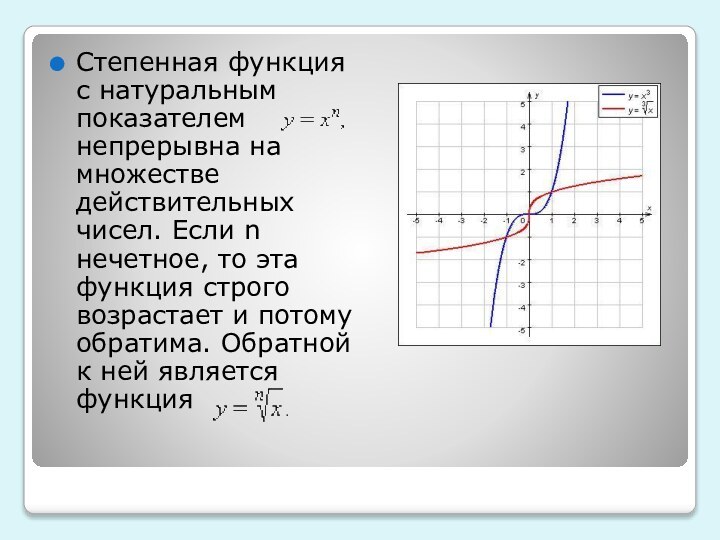
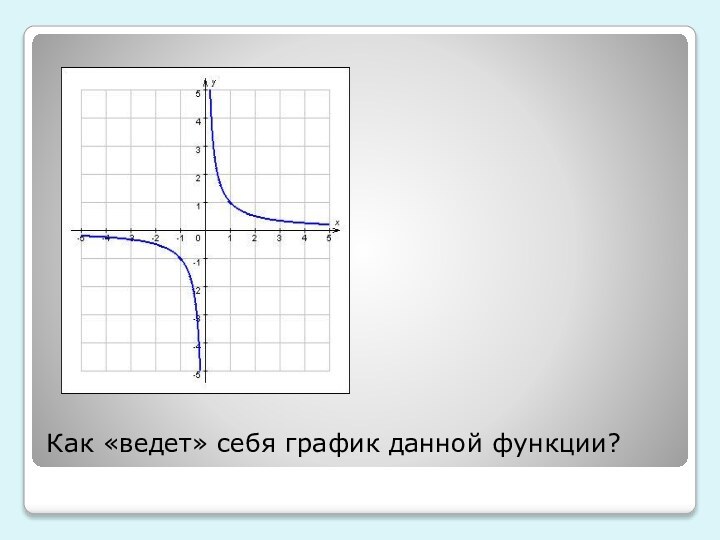
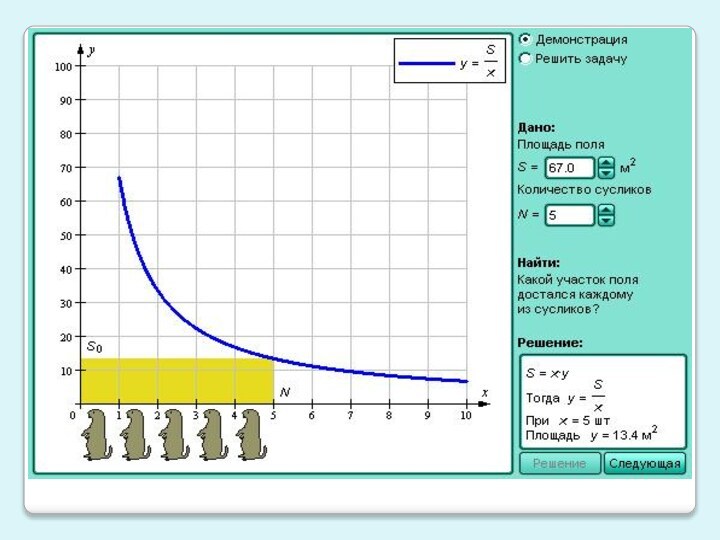
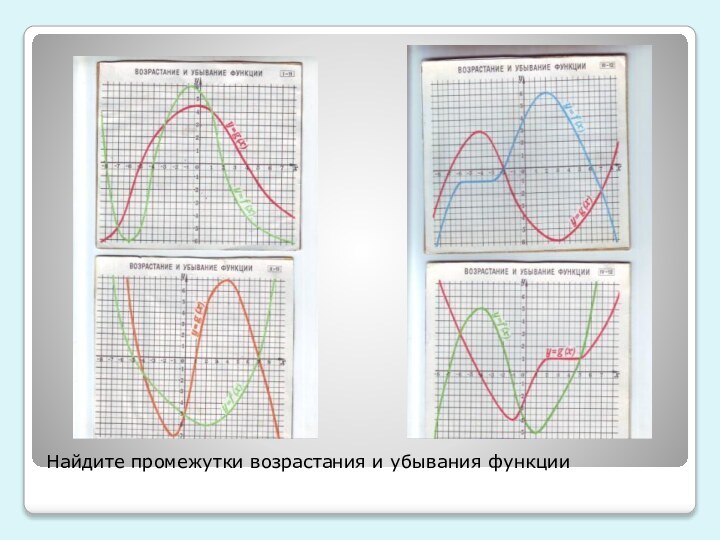
убывающей, постоянной функции. Привести примеры таких графиков
2)Показать некоторые степенные
функции3)Исследовать графики разных функций на возрастание и убывание
4) Показать связь данных понятий с жизнью