Биография великих математиков Чевы и Менелая
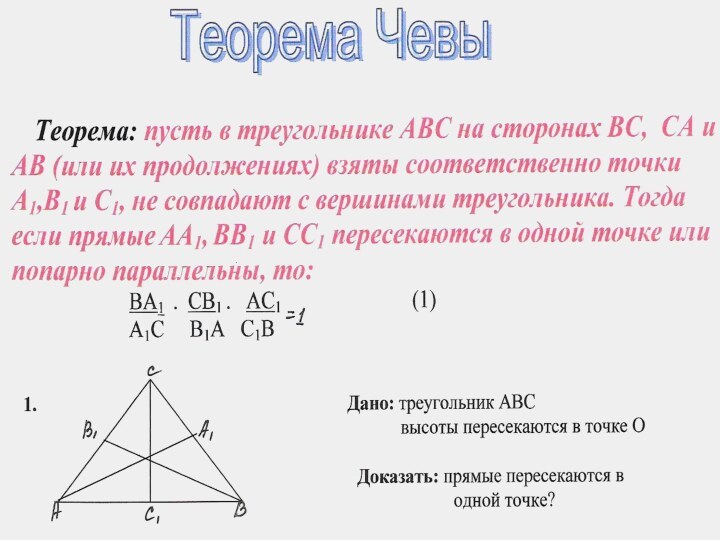
Теорема Чевы
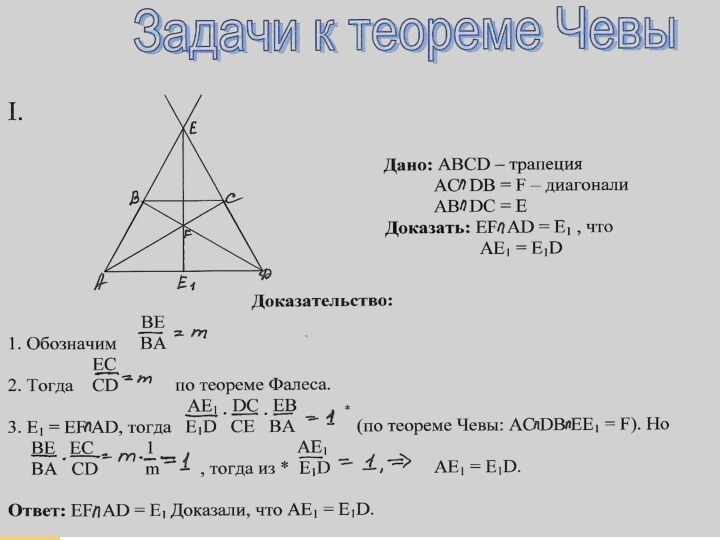
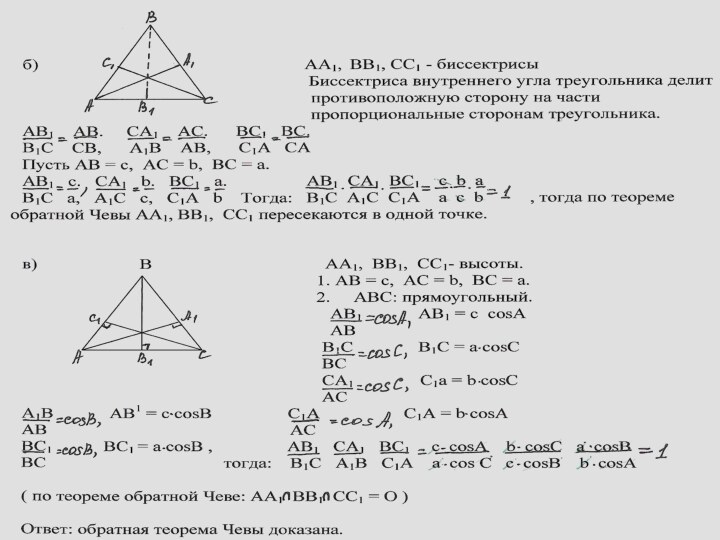
Задачи к теореме Чевы
Теорема Менелая
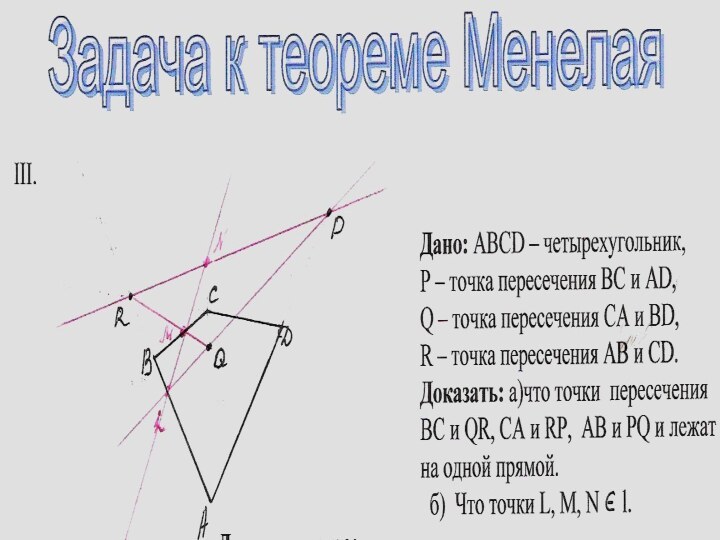
Задача к теореме Менелая
Литература
Слайд 3
Введение
В курсе геометрии были рассмотрены важные
и интересные свойства геометрических фигур на плоскости. Но многие
удивительные соотношения и изящные геометрические факты не вошли в основной курс. Здесь мы рассмотрим еще несколько замечательных теорем планиметрии.
Мы знаем, что: медианы треугольника пересекаются в одной точки; биссектрисы треугольника пересекаются в одной точке; высоты треугольника (или их продолжениях) пересекаются в одной точке.
Поставим теперь более общий вопрос. Рассмотрим треугольник ABC и отметим на его сторонах BC,CA и AB (или их продолжениях) точки A1,B1 и C1. При каком расположении этих точек прямые AA1, BB1 и CC1 пересекаются в одной точке или будут лежать на одной прямой?
Эти вопросы были решены математиками Чевой и Менелаем.
Слайд 4
Джованни Чева ( 1648-1734 ) – итальянский математик.
Основной заслугой Чевы является построение учения о секущих прямых,
которое положило начало новой синтетической геометрии; оно изложено в сочинении «О взаимопересекающихся прямых» (1678 году).
Слайд 5
Менелай Александрийский, древнегреческий астролог и математик ( I
века ). Автор работ по сферической тригонометрии: 6 книг о
вычислении хорд и 3 книги «Сферики» ( сохранились только в арабском переводе ). Тригонометрия у Менелая отделена от астрологии и геометрии. Арабские авторы упоминают также о книге Менелая по гидростатике.