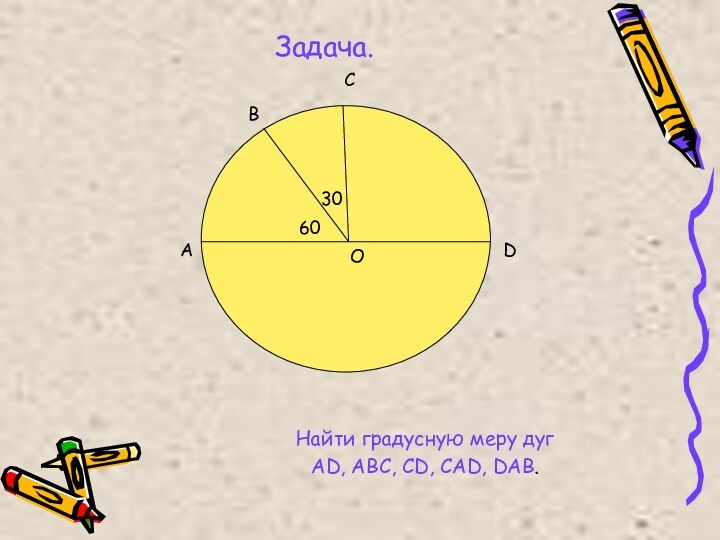
окружность?
Что такое радиус окружности?
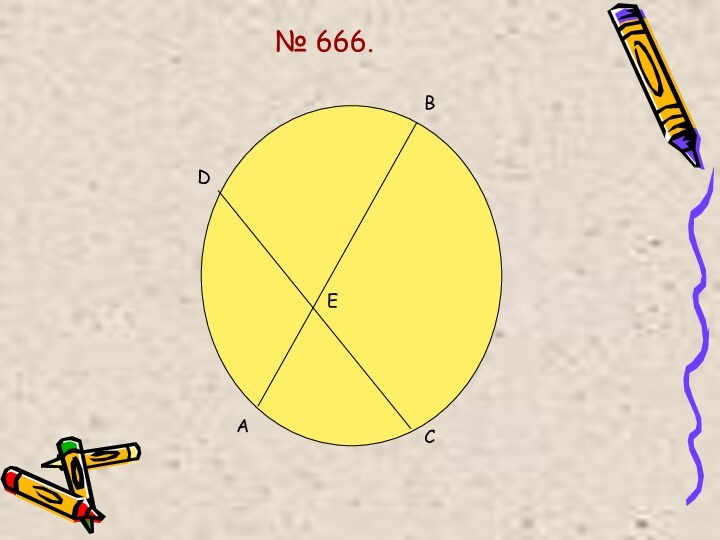
Что такое диаметр окружности?
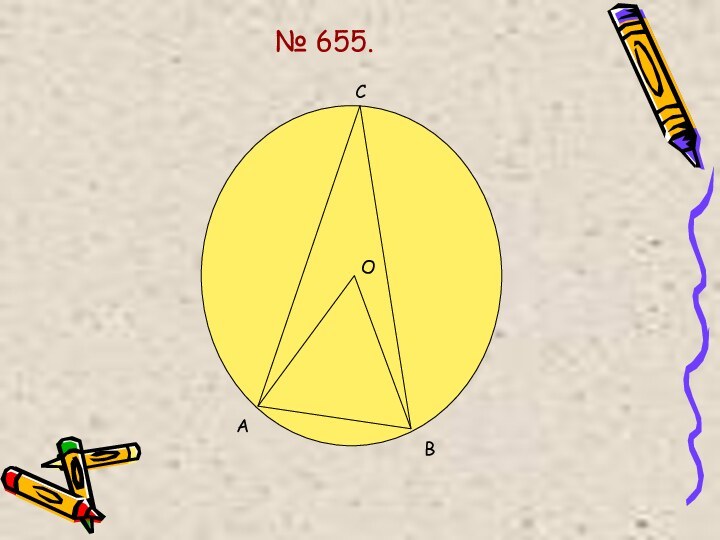
Что такое хорда
окружности?Прямая и окружность:
Не пересекаются, если расстояние от центра окружности до прямой больше радиуса
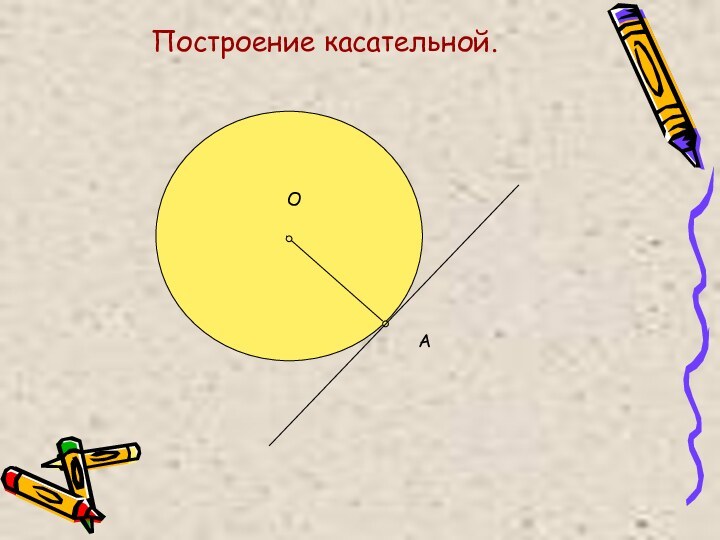
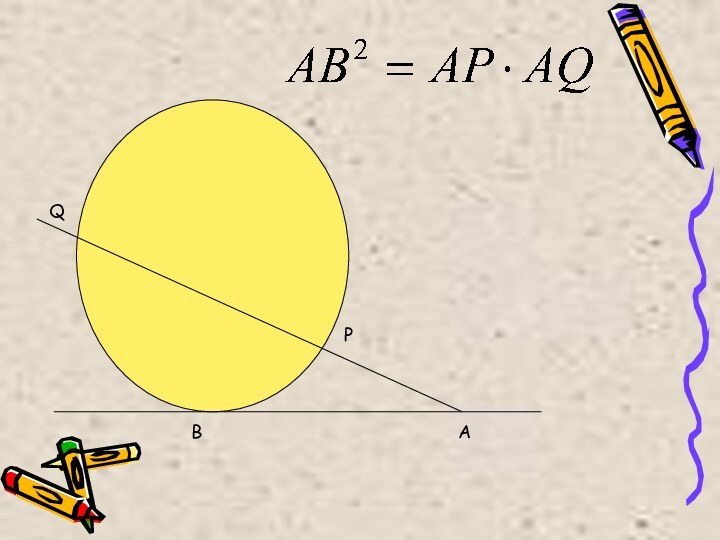
Касаются, если расстояние от центра окружности до прямой равно радиусу (имеют одну общую точку – точку касания).
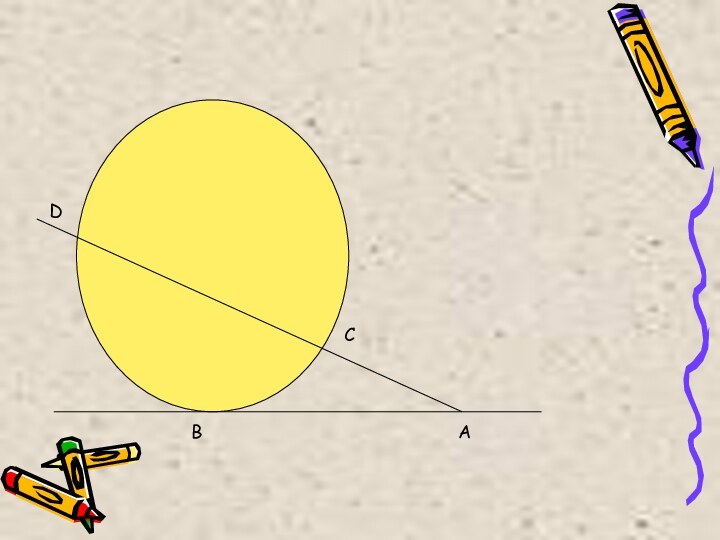
Пересекаются в двух точках, если расстояние от центра окружности до прямой меньше радиуса.