- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему История развития математики
Содержание
- 2. СодержаниеМатематика - это ?Возникновение арифметики и геометрииДревний ВостокВавилонДревняя ГрецияЗаключение
- 3. Математика - это наука, исторически основанная на
- 4. Математика в системе человеческих знаний есть раздел,
- 5. Египет Древнейшие древнеегипетские математические тексты относятся к
- 6. Египтяне писали на папирусе, который сохраняется плохо,
- 7. В области геометрии египтяне знали точные формулы
- 8. Иероглифическая запись уравнения
- 9. ВавилонВавилоняне писали клинописными значками на глиняных табличках,
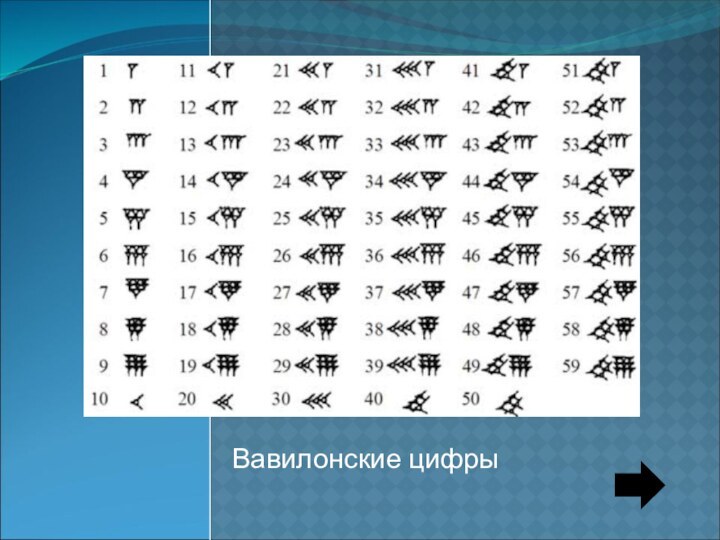
- 10. Вавилонские цифры
- 11. Вавилонская расчётная техника была намного совершеннее египетской,
- 12. Шумеры и вавилоняне использовали 60-ричную позиционную систему
- 13. Математика в современном понимании этого слова родилась
- 14. Попытка пифагорейцев положить в основу мировой гармонии
- 15. Греческая математика впечатляет прежде всего богатством содержания.
- 16. Скачать презентацию
- 17. Похожие презентации
СодержаниеМатематика - это ?Возникновение арифметики и геометрииДревний ВостокВавилонДревняя ГрецияЗаключение















Слайд 2
Содержание
Математика - это ?
Возникновение арифметики и геометрии
Древний Восток
Вавилон
Древняя
Греция
Слайд 3 Математика - это наука, исторически основанная на решении
задач о количественных и пространственных соотношениях реального мира путём
идеализации необходимых для этого свойств объектов и формализации этих задач.Слайд 4 Математика в системе человеческих знаний есть раздел, занимающийся
такими понятиями, как количество, структура, соотношение и т. п. Развитие
математики началось с создания практических искусств счёта и измерения линий, поверхностей и объёмов.Счёт долгое время оставался только вещественным — использовались пальцы, камешки, пометки и т. п.
С распространением счёта на большие количества появилась идея считать не только единицами, но и пакетами единиц, содержащими, например, 10 объектов. Эта идея немедленно отразилась в языке, а затем и в письменности.
Слайд 5
Египет
Древнейшие древнеегипетские математические тексты относятся к началу
II тысячелетия до н. э. Математика тогда использовалась в астрономии,
мореплавании, землемерии, при строительстве домов, плотин, каналов и военных укреплений. Денежных расчётов, как и самих денег, в Египте не было.Слайд 6 Египтяне писали на папирусе, который сохраняется плохо, и
поэтому в настоящее время знаний о математике Египта существенно
меньше, чем о математике Вавилона или Греции. Вероятно, она была развита лучше, чем можно представить, исходя из дошедших до нас документов, что подтверждается тем, что греческие математики учились у египтян.Основные сохранившиеся источники: папирус Ахмеса, он же папирус Ринда (84 математические задачи), и московский папирус Голенищева (25 задач).
Слайд 7 В области геометрии египтяне знали точные формулы для
площади прямоугольника, треугольника и трапеции.
Площадь круга вычислялась, исходя
из предположения П = 3,1605 (погрешность менее 1 %).Египтяне знали точные формулы для объёма параллелепипеда и различных цилиндрических тел, а также пирамиды и усечённой пирамиды.
О более раннем ходе развития математики в Египте сведений нет никаких.
Слайд 9
Вавилон
Вавилоняне писали клинописными значками на глиняных табличках, которые
в немалом количестве дошли до наших дней (более 500000,
из них около 400 связаны с математикой). Поэтому мы имеем довольно полное представление о математических достижениях учёных Вавилонского государства. Отметим, что корни культуры вавилонян были в значительной степени унаследованы от шумеров — клинописное письмо, счётная методика и т. п.Слайд 11 Вавилонская расчётная техника была намного совершеннее египетской, а
круг решаемых задач существенно шире. Есть задачи на решение
уравнений второй степени, геометрические прогрессии. При решении применялись пропорции, средние арифметические, проценты. Методы работы с прогрессиями были глубже, чем у египтян.Встречаются также кубические уравнения и системы линейных уравнений. Венцом планиметрии была теорема Пифагора.
Слайд 12 Шумеры и вавилоняне использовали 60-ричную позиционную систему счисления,
увековеченную в нашем делении круга на 360°, часа на
60 минут и минуты на 60 секунд.В геометрии рассматривались те же фигуры, что и в Египте, плюс сегмент круга и усечённый конус. Вавилоняне умели вычислять площади правильных многоугольников.
Слайд 13 Математика в современном понимании этого слова родилась в
Греции. Греки подошли к использованию математики таким образом.
Во-первых, пифагорейская
школа выдвинула тезис «Числа правят миром». Или, как сформулировали эту же мысль два тысячелетия спустя: «Природа разговаривает с нами на языке математики» (Галилей). Во-вторых, для открытия таких истин пифагорейцы разработали законченную методологию. Сначала они составили список первичных, интуитивно очевидных математических истин (аксиомы, постулаты). Затем с помощью логических рассуждений из этих истин выводились новые утверждения, которые также обязаны быть истинными. Так появилась дедуктивная математика.
Греки проверили справедливость этого тезиса во многих областях: астрономия, оптика, музыка, геометрия, позже — механика.
Слайд 14 Попытка пифагорейцев положить в основу мировой гармонии целые
числа была поставлена под сомнение после того, как были
обнаружены иррациональные числа. Платоновская школа (IV век до н. э.) выбрала иной, геометрический фундамент математики. На этом пути были достигнуты величайшие успехи античной математики (Евклид, Архимед, Аполлоний Пергский и другие).Слайд 15 Греческая математика впечатляет прежде всего богатством содержания. Зачатки
анализа заметны у Архимеда, корни алгебры — у Диофанта,
аналитическая геометрия — у Аполлония и т. д. Но главное не в этом. Два достижения греческой математики далеко пережили своих творцов.Первое — греки построили математику как целостную науку с собственной методологией, основанной на чётко сформулированных законах логики (гарантирующих истинность выводов при условии, что истинны предпосылки).
Второе — они провозгласили, что законы природы постижимы для человеческого разума, и математические модели — ключ к их познанию.
В этих двух отношениях древнегреческая математика вполне родственна современной.