Слайд 2
Просторові геометричні фігури
Прямокутний паралелепіпед – це просторова геометрична
фігура, яка обмежена шістьма прямокутниками, що називаються гранями.
Сторони прямокутників
називаються ребрами прямокутного паралелепіпеда, а вершини прямокутників – вершинами прямокутного паралелепіпеда. Верхню і нижню грані прямокутного паралелепіпеда називають основами, а ребра цих граней – ребрами основи, інші ребра називають бічними ребрами, а інші грані – бічними гранями.
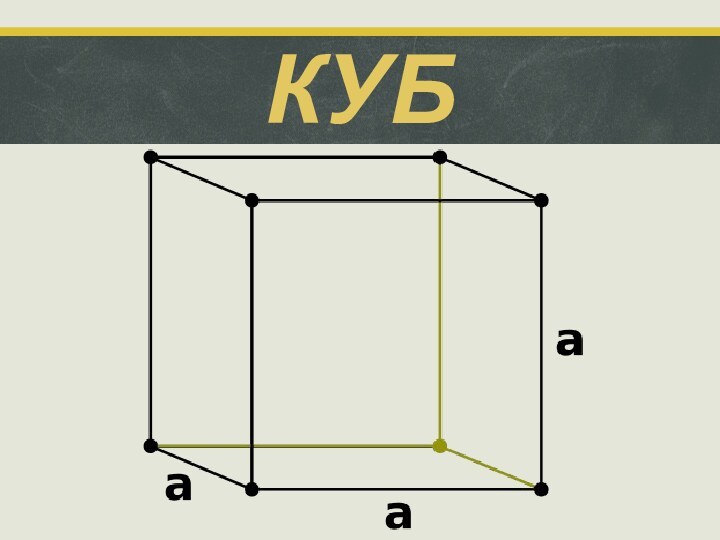
Куб – це прямокутний паралелепіпед, у якого всі шість граней – квадрати.
Слайд 4
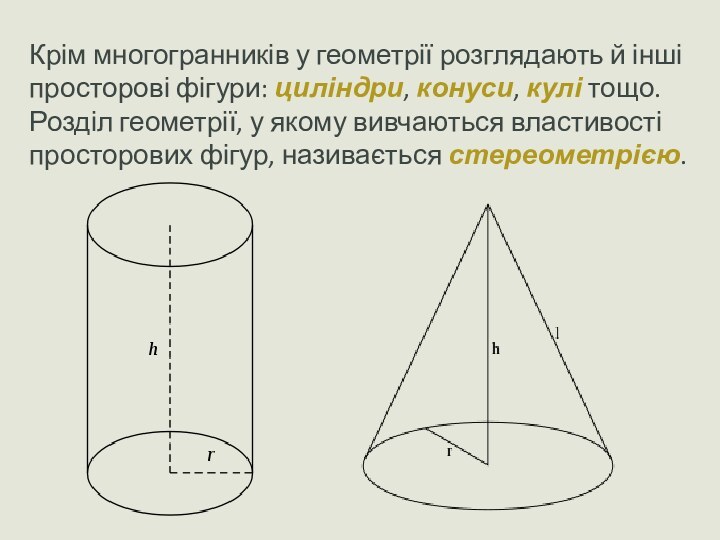
Крім многогранників у геометрії розглядають й інші просторові
фігури: циліндри, конуси, кулі тощо.
Розділ геометрії, у якому вивчаються
властивості просторових фігур, називається стереометрією.
Слайд 5
Основні просторові фігури
Основними фігурами простору є точка, пряма
і площина.
Пригадаємо, що точки позначають великими латинськими буквами, наприклад,
- А,В,С…, прямі позначають малими латинськими буквами, наприклад, - прямі а,в,с…, або двома великими буквами,наприклад, - прямі АВ, ВС, …. Зображують площину у вигляді паралелограма або у вигляді довільної області і позначають площини малими грецькими буквами, наприклад – площини α, β, γ.
Слайд 6
Основні аксіоми стереометрії
Властивості основних фігур у стереометрії виражаються
аксіомами.
Аксіома 1. Яка б не була площина, існують точки,
які належать цій площині, і точки які їй не належать.
Аксіома 2. Якщо дві різні площини мають спільну точку, то вони перетинаються по прямій, що проходить через цю точку.
Аксіома 3. Якщо дві різні прямі мають спільну точку, то через них можна провести площину і до того ж тільки одну.
Ніяких інструментів, якими б можна було побудувати в просторі площину, немає. Тому вираз «можна провести площину» вживається в значенні «існує площина».
Слайд 9
Взаємне розміщення двох прямих у просторі
Із планіметрії відомо,
що дві прямі, що лежать у площині, можуть перетинатися
або не мати спільних точок. Якщо дві прямі лежать одній площині й не мають спільних точок, то вони називаються паралельними. У просторі дві різні прямі або перетинаються, або не перетинаються. Проте другий випадок допускає дві можливості: прямі лежать в одній площині або прямі не лежать в одній площині.
Прямі, які не перетинаються і лежать в одній площині, називаються паралельними.
Прямі, які не перетинаються і не лежать в одній площині, називаються мимобіжними.
(Випадки взаємного розташування двох прямих у просторі демонструються за допомогою стереометричного ящика або на каркасній моделі куба).
Отже, дві прямі а і в в просторі можуть перетинатися, бути паралельними, бути мимобіжними.
Слайд 10
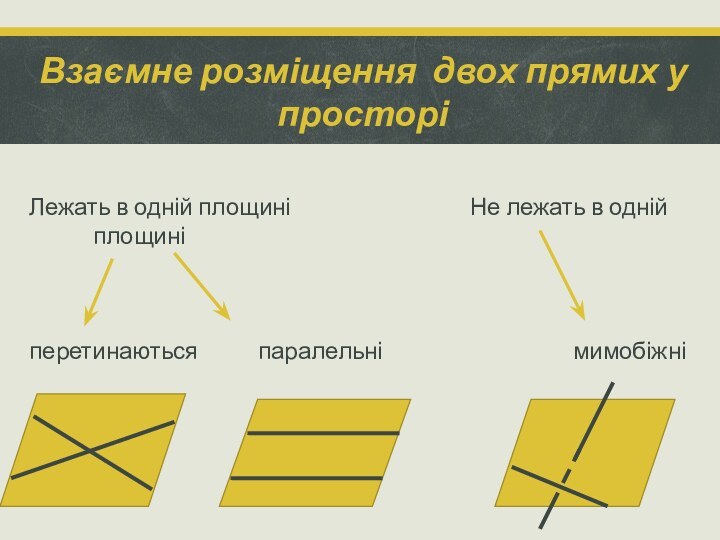
Взаємне розміщення двох прямих у просторі
Лежать в одній
площині
Не лежать в одній площині
перетинаються паралельні мимобіжні
Слайд 11
Взаємне розміщення двох площин
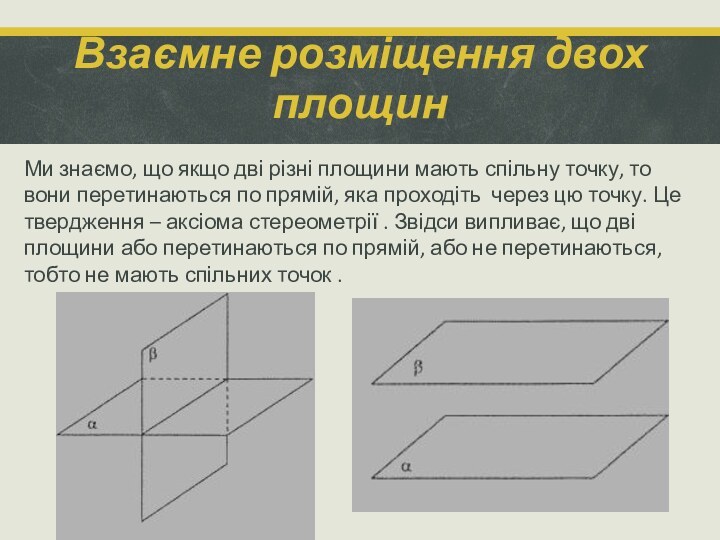
Ми знаємо, що якщо дві
різні площини мають спільну точку, то вони перетинаються по
прямій, яка проходіть через цю точку. Це твердження – аксіома стереометрії . Звідси випливає, що дві площини або перетинаються по прямій, або не перетинаються, тобто не мають спільних точок .
Слайд 12
Взаємне розміщення двох площин
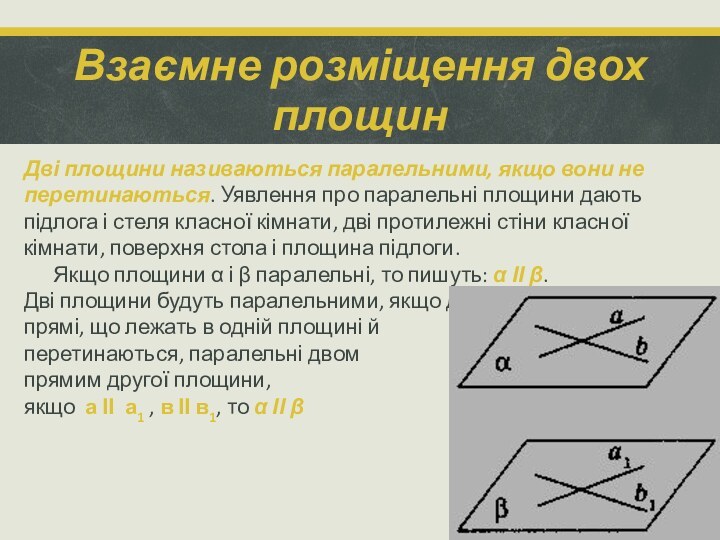
Дві площини називаються паралельними, якщо
вони не перетинаються. Уявлення про паралельні площини дають підлога
і стеля класної кімнати, дві протилежні стіни класної кімнати, поверхня стола і площина підлоги.
Якщо площини α і β паралельні, то пишуть: α ІІ β.
Дві площини будуть паралельними, якщо дві прямі, що лежать в одній площині й перетинаються, паралельні двом прямим другої площини, тобто якщо а ІІ а1 , в ІІ в1, то α ІІ β
Слайд 13
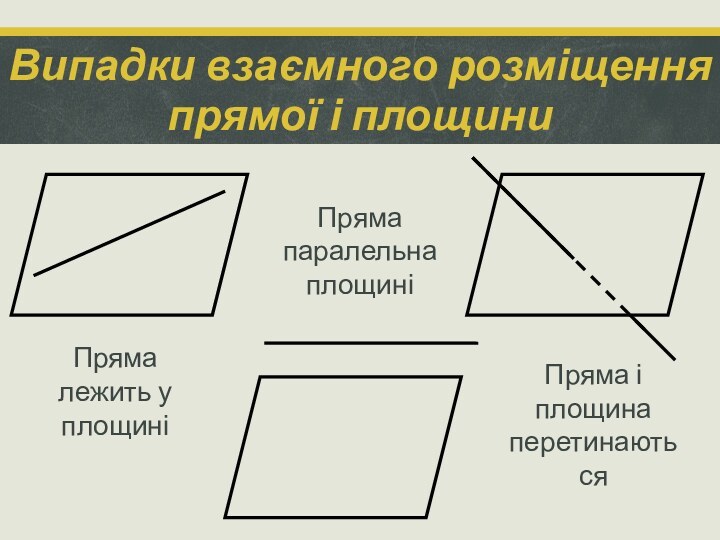
Випадки взаємного розміщення прямої і площини
Пряма лежить у
площині
Пряма паралельна площині
Пряма і площина перетинаються
Слайд 14
Випадки взаємного розміщення прямої і площини
с
в
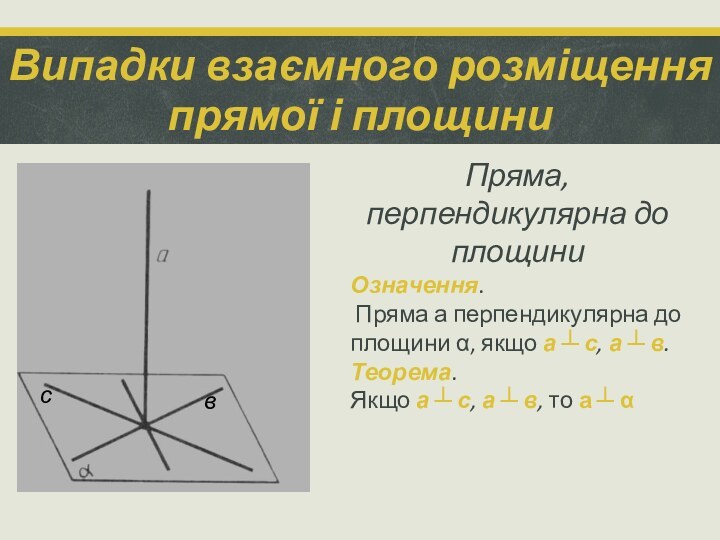
Пряма, перпендикулярна до
площини
Означення.
Пряма а перпендикулярна до площини α, якщо а
┴ с, а ┴ в.
Теорема.
Якщо а ┴ с, а ┴ в, то а ┴ α