Слайд 2
Как известно…
Теорема Пифагора звучит так: «В прямоугольном треугольнике
квадрат гипотенузы равен сумме квадратов его катетов», но…
Как звучала
эта теорема у Евклида: «В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол »
Как звучала у Аннаирици: «Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол»
Слайд 3
Научное открытие
В настоящее время известно, что эта теорема
не была открыта Пифагором. Однако одни полагают, что Пифатор
первым дал ее полноценное докзательство, а другие отказывают ему и в этой заслуге. Некоторые приписывают Пифагору доказательство, которое Евклид приводит в первой книге своих "Начал". С другой стороны, Прокл утверждает, что доказательство в "Началах" принадлежит самому Евклиду. Как мы видим, история математики почти не сохранила достоверных данных о жизни Пифагора и его математической деятельности. Зато легенда сообщает даже ближайшие обстоятельства, сопровождавшие открытие теоремы. Многим известен сонет Шамиссо:
Слайд 4
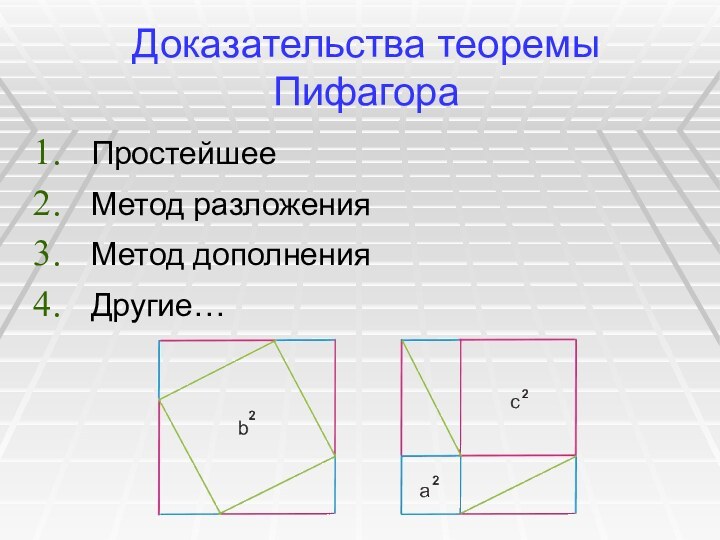
Доказательства теоремы Пифагора
Простейшее
Метод разложения
Метод дополнения
Другие…
Слайд 5
Простейшее доказательство
Простейшее доказательство теоремы получается в простейшем случае
равнобедренного прямоугольного треугольника. В самом деле, достаточно просто посмотреть
на мозаику равнобедренных прямоугольных треугольников , чтобы убедиться в справедливости теоремы. Например, для треугольника ABC : квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах,- по два.
Теорема доказана.
Слайд 6
Доказательство методом дополнения
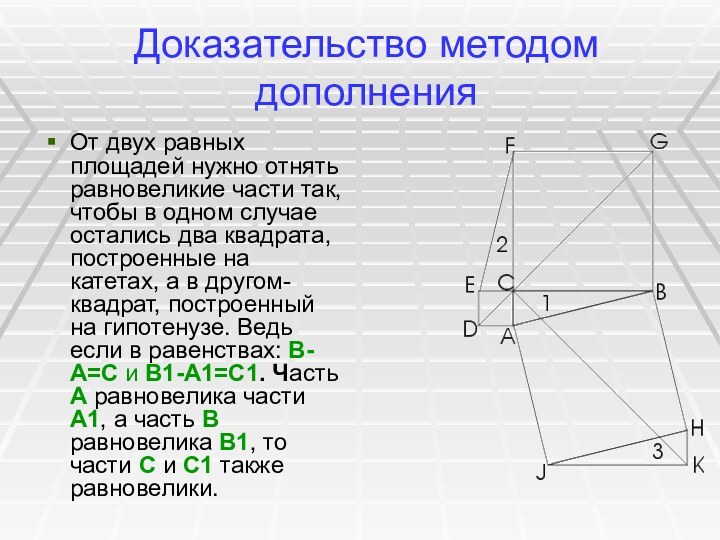
От двух равных площадей нужно отнять
равновеликие части так, чтобы в одном случае остались два
квадрата, построенные на катетах, а в другом- квадрат, построенный на гипотенузе. Ведь если в равенствах: В-А=С и В1-А1=С1. Часть А равновелика части А1, а часть В равновелика В1, то части С и С1 также равновелики.
Слайд 7
Доказательство методом дополнения
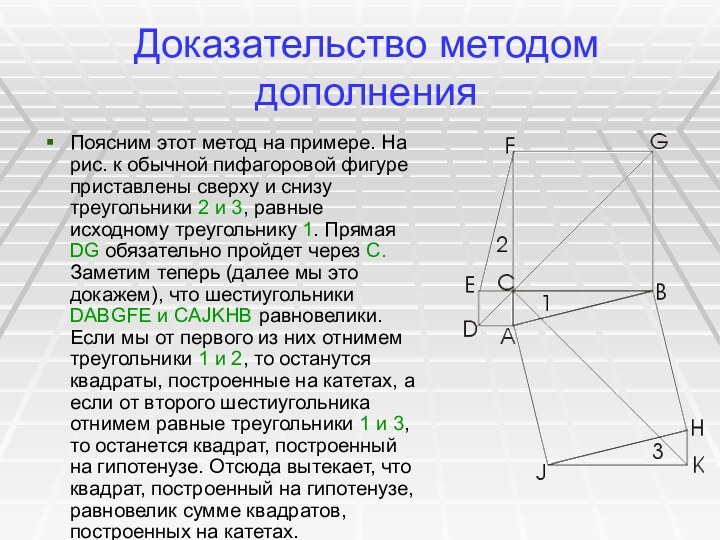
Поясним этот метод на примере. На
рис. к обычной пифагоровой фигуре приставлены сверху и снизу
треугольники 2 и 3, равные исходному треугольнику 1. Прямая DG обязательно пройдет через C. Заметим теперь (далее мы это докажем), что шестиугольники DABGFE и CAJKHB равновелики. Если мы от первого из них отнимем треугольники 1 и 2, то останутся квадраты, построенные на катетах, а если от второго шестиугольника отнимем равные треугольники 1 и 3, то останется квадрат, построенный на гипотенузе. Отсюда вытекает, что квадрат, построенный на гипотенузе, равновелик сумме квадратов,построенных на катетах.
Слайд 8
Доказательство методом дополнения
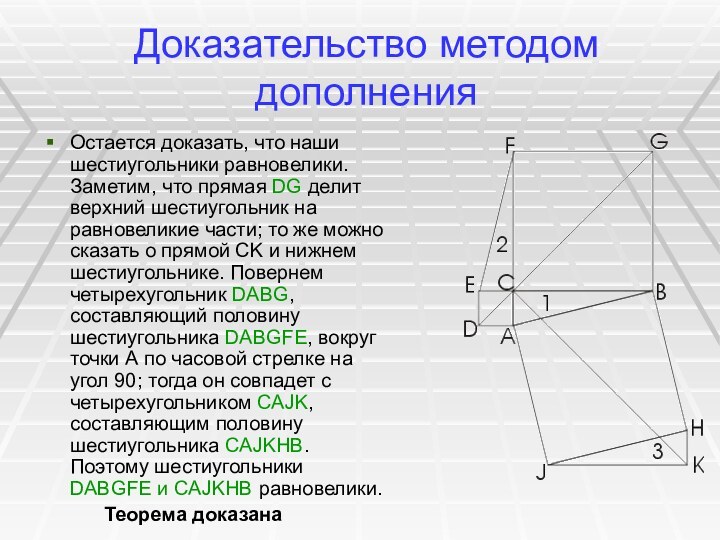
Остается доказать, что наши шестиугольники равновелики.
Заметим, что прямая DG делит верхний шестиугольник на равновеликие
части; то же можно сказать о прямой CK и нижнем шестиугольнике. Повернем четырехугольник DABG, составляющий половину шестиугольника DABGFE, вокруг точки А по часовой стрелке на угол 90; тогда он совпадет с четырехугольником CAJK, составляющим половину шестиугольника CAJKHB. Поэтому шестиугольники DABGFE и CAJKHB равновелики.
Теорема доказана
Слайд 9
Доказательство методом вычитания
Знакомый нам чертеж теоремы Пифагора
заключим в прямоугольную рамку, направления сторон которой совпадают с
направлениями катетов треугольника. Продолжим некоторые из отрезков фигуры так, как указано на рисунке, при этом прямоугольник распадается на несколько треугольников, прямоугольников и квадратов. Выбросим из прямоугольника сначала несколько частей так чтобы остался лишь квадрат, построенный на гипотенузе. Эти части следующие:
Слайд 10
Доказательство методом вычитания
треугольники 1, 2, 3, 4;
прямоугольник
5;
прямоугольник 6 и квадрат 8;
прямоугольник 7 и
квадрат 9;
Затем выбросим из прямоугольника части так, чтобы остались только квадраты, построенные на катетах. Этими частями будут:
прямоугольники 6 и 7;
прямоугольник 5;
прямоугольник 1(заштрихован);
прямоугольник 2(заштрихован);
Слайд 11
Доказательство методом вычитания
Нам осталось лишь показать, что отнятые
части равновелики. Это легко видеть в силу расположения фигур.
Из рисунка ясно, что:
прямоугольник 5 равновелик самому себе;
четыре треугольника 1,2,3,4 равновелики двум прямоугольникам 6 и 7;
прямоугольник 6 и квадрат 8, взятые вместе, равновелики прямоугольнику 1 (заштрихован);;
прямоугольник 7 вместе с квадратом 9 равновелики прямоугольнику 2(заштрихован);
Доказательство закончено
Слайд 12
Доказательство Хоукинсa
Прямоугольный треугольник ABC с прямым углом
C повернем на 90° так, чтобы он занял положение
A'CB'. Продолжим гипотенузу A'В' за точку A' до пересечения с линией АВ в точке D. Отрезок В'D будет высотой треугольника В'АВ. Рассмотрим теперь заштрихованный четырехугольник A'АВ'В . Его можно разложить на два равнобедренных треугольника САA' и СВВ' (или на два треугольника A'В'А и A'В'В).
Слайд 13
Доказательство Хоукинсa
SCAA'=b²/2, SCBB'=a²/2
SA'AB'B=(a²+b²)/2
Треугольники A'В'А и A'В'В имеют общее
основание с и высоты DA
и DB, поэтому :
SA'AB'B=c*DA/2+ c*DB/2=c(DA+DB)/2=c²/2
Сравнивая
два полученных выражения для площади, получим:
a²+b²=c²
Теорема доказана.
Слайд 14
Векторное доказательство
Пусть АВС - прямоугольный треугольник с прямым
углом при вершине С, построенный на векторах. Тогда справедливо
векторное равенство:b+c=a
откуда имеем
c = a - b
возводя обе части в квадрат, получим
c²=a²+b²-2ab
Так как a перпендикулярно b, то ab=0, откуда
c²=a²+b² или c²=a²+b²
Нами снова доказана теорема Пифагора.
Если треугольник АВС - произвольный, то та же формула дает т. н. теорему косинусов, обобщающую теорему Пифагора.
Слайд 15
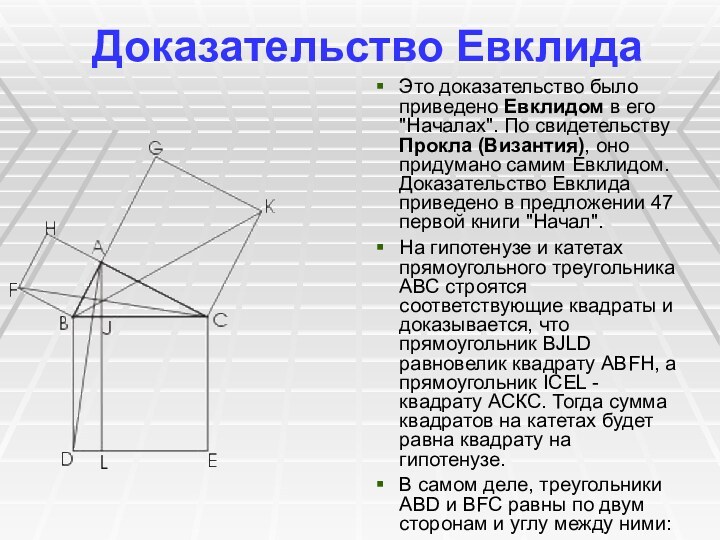
Доказательство Евклида
Это доказательство было приведено Евклидом в
его "Началах". По свидетельству Прокла (Византия), оно придумано самим
Евклидом. Доказательство Евклида приведено в предложении 47 первой книги "Начал".
На гипотенузе и катетах прямоугольного треугольника АВС строятся соответствующие квадраты и доказывается, что прямоугольник BJLD равновелик квадрату ABFH, а прямоугольник ICEL - квадрату АСКС. Тогда сумма квадратов на катетах будет равна квадрату на гипотенузе.
В самом деле, треугольники ABD и BFC равны по двум сторонам и углу между ними:
Слайд 16
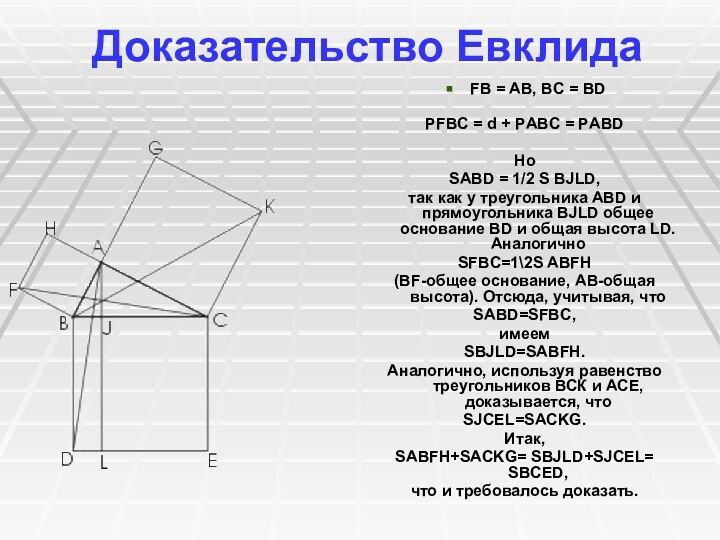
Доказательство Евклида
FB = AB, BC = BD
РFBC = d + РABC = РABD
Но
SABD = 1/2 S BJLD,
так как у треугольника ABD
и прямоугольника BJLD общее основание BD и общая высота
LD. Аналогично
SFBC=1\2S ABFH
(BF-общее основание, АВ-общая высота). Отсюда, учитывая, что
SABD=SFBC,
имеем
SBJLD=SABFH.
Аналогично, используя равенство треугольников ВСК и АСЕ, доказывается, что
SJCEL=SACKG.
Итак,
SABFH+SACKG= SBJLD+SJCEL= SBCED,
что и требовалось доказать.
Слайд 17
Удивительный факт
Вопрос о том, можно ли с помощью
световых сигналов объясняться с этими гипотетическими существами, вызвал оживленную
дискуссию. Парижской академией наук была даже установлена премия в 100000 франков тому, кто первый установит связь с каким-нибудь обитателем другого небесного тела; эта премия все еще ждет счастливца. В шутку, хотя и не совсем безосновательно , было решено передать обитателям Марса сигнал в виде теоремы Пифагора.
Неизвестно, как это сделать; но для всех очевидно, что математический факт, выражаемый теоремой Пифагора имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.