Презентация на тему Задача Эйлера

Содержание

2. Теорема ЭйлераТеорема. Для связного простого графа имеет
3. Решение задачи ЭйлераПредположим, что можно провести непересекающиеся
4. Упражнение 1Посчитайте число вершин (В), ребер (Р)
5. Упражнение 2Посчитайте число вершин (В), ребер (Р)
6. Упражнение 3Два соседа имеют: а) три общих
7. Упражнение 4Три соседа имеют: а) два общих
8. Упражнение 5Четыре соседа имеют четыре общих колодца.
9. Скачать презентацию
10. Похожие презентации

Теорема ЭйлераТеорема. Для связного простого графа имеет место равенство В - Р + Г = 2, где В - число вершин, Р - общее число ребер, Г - число областей (граней), на которые граф разбивает плоскость.Доказательство.

Задача ЭйлераЗадача. Три соседа имеют три общих колодца. Можно ли провести непересекающиеся

Решение задачи ЭйлераПредположим, что можно провести непересекающиеся дорожки от каждого дома к

Упражнение 1Посчитайте число вершин (В), ребер (Р) и областей (Г) для графов,

Упражнение 2Посчитайте число вершин (В), ребер (Р) и граней (Г) для многогранников,

Упражнение 3Два соседа имеют: а) три общих колодца; б) четыре общих колодца.

Упражнение 4Три соседа имеют: а) два общих колодца; б) четыре общих колодца.

Упражнение 5Четыре соседа имеют четыре общих колодца. Можно ли провести непересекающиеся дорожки

Упражнение 6Докажите, что пять домиков нельзя соединить непересекающимися дорожками так, чтобы каждый

Слайды презентации

Слайд 2 Теорема Эйлера
Теорема. Для связного простого графа имеет место

Теорема ЭйлераТеорема. Для связного простого графа имеет место равенство В -

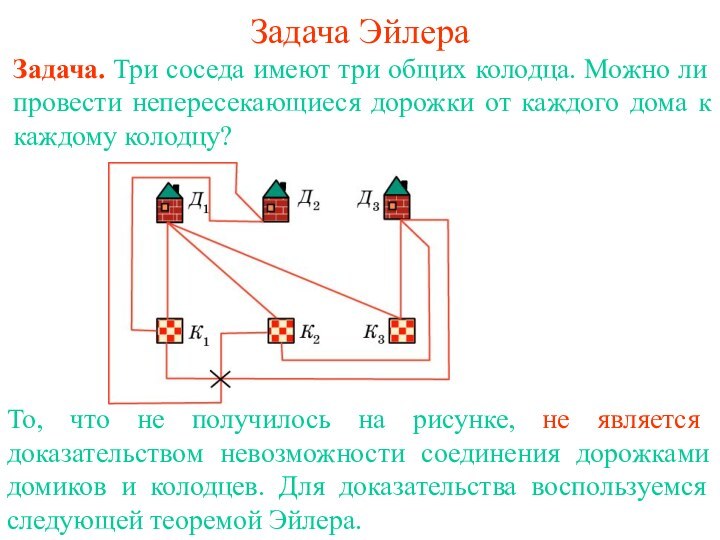
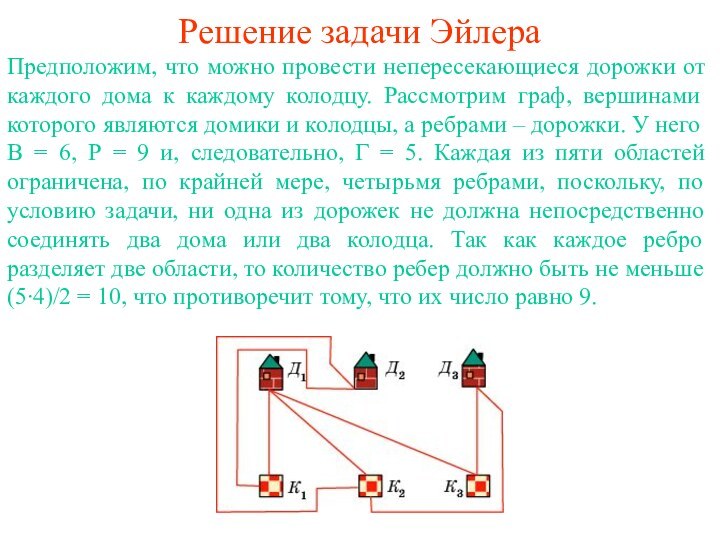
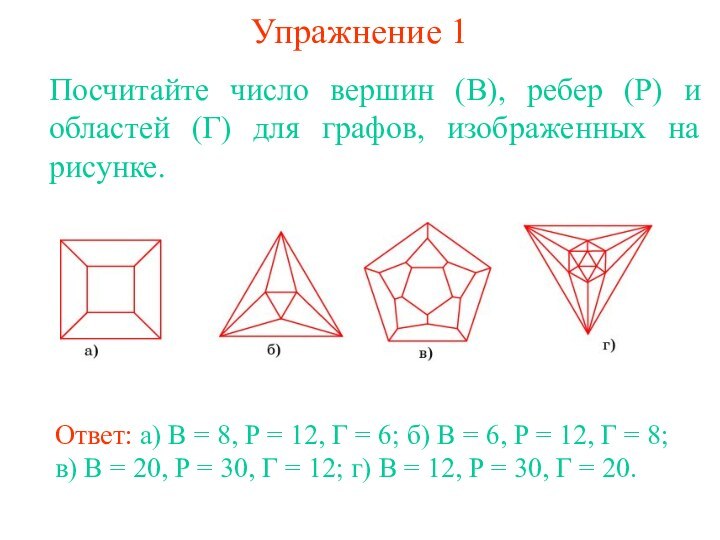
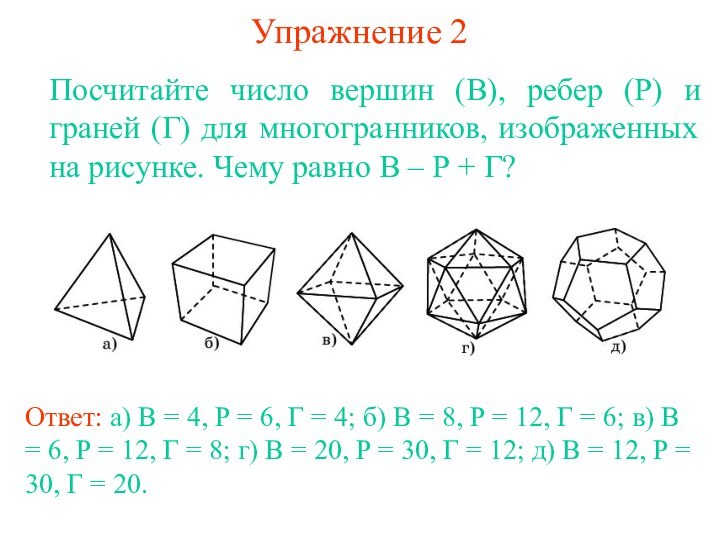
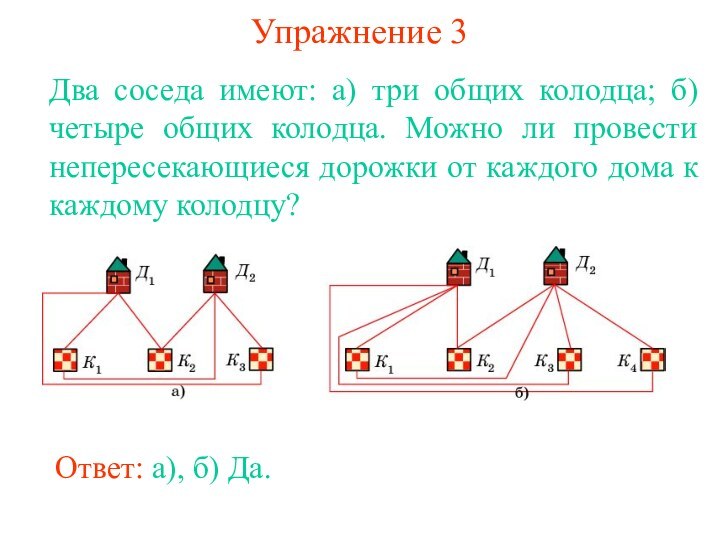
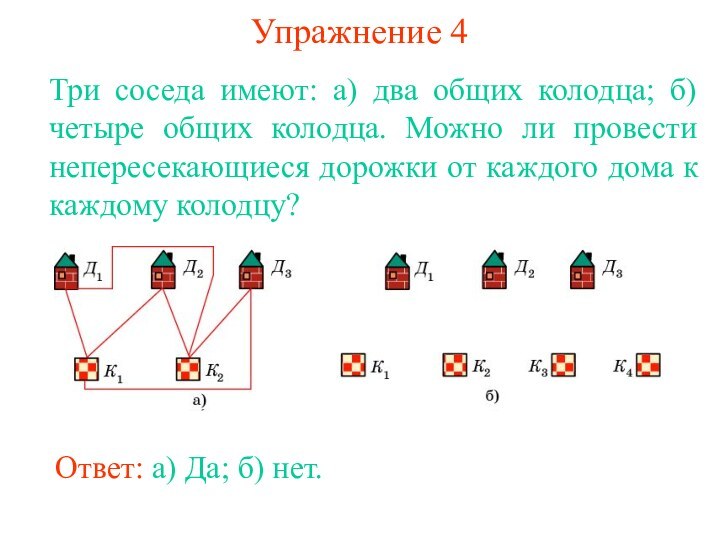
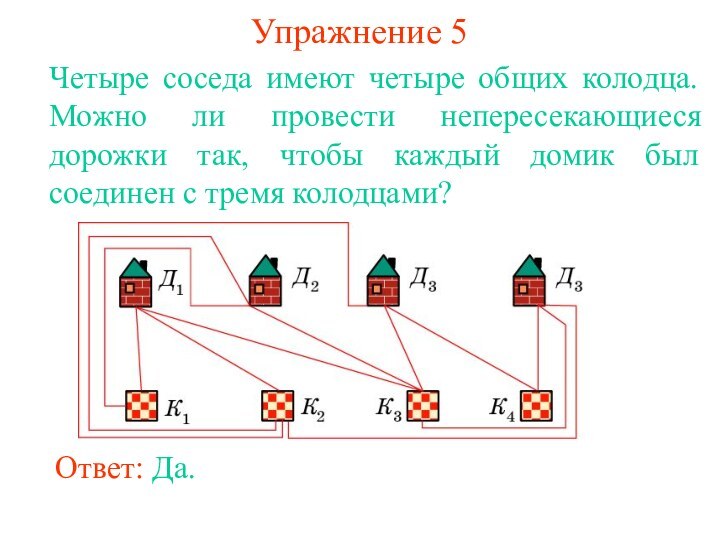
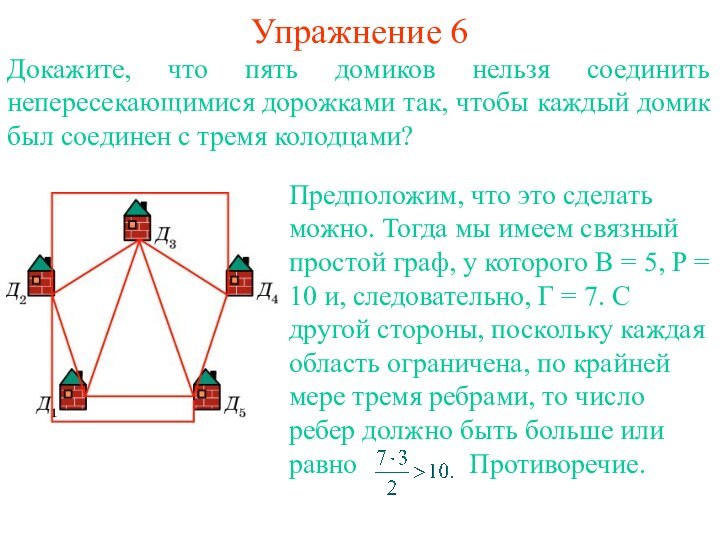
равенство В - Р + Г = 2, где

В - число вершин, Р - общее число ребер, Г - число областей (граней), на которые граф разбивает плоскость.

Доказательство. Стянем какое-нибудь ребро графа, соединяющее две вершины, в точку. При этом число ребер и число вершин уменьшаться на единицу и, следовательно, В – Р + Г не измениться. Продолжая стягивать ребра, мы придем к графу, у которого имеется одна вершина, а ребрами являются петли. Уберем какое-нибудь ребро. При этом число ребер и число областей уменьшаться на единицу и, следовательно, В – Р + Г не изменится. Продолжая убирать ребра, мы придем к графу, у которого имеется одна вершина и одно ребро. У этого графа В = 1, Р = 1, Г = 2 и, следовательно, В – Р + Г = 2. Значит, для исходного графа также выполняется равенство В – Р + Г = 2.

Слайд 3 Решение задачи Эйлера
Предположим, что можно провести непересекающиеся дорожки

Решение задачи ЭйлераПредположим, что можно провести непересекающиеся дорожки от каждого дома

от каждого дома к каждому колодцу. Рассмотрим граф, вершинами

которого являются домики и колодцы, а ребрами – дорожки. У него В = 6, Р = 9 и, следовательно, Г = 5. Каждая из пяти областей ограничена, по крайней мере, четырьмя ребрами, поскольку, по условию задачи, ни одна из дорожек не должна непосредственно соединять два дома или два колодца. Так как каждое ребро разделяет две области, то количество ребер должно быть не меньше (5∙4)/2 = 10, что противоречит тому, что их число равно 9.