Презентация на тему Задача о назначениях. Алгоритмы

оптимизации в области математической оптимизации или исследовании операций. Задача

состоит в поиске минимальной суммы дуг во взвешенном двудольном графе.

В наиболее общей форме задача формулируется следующим образом:

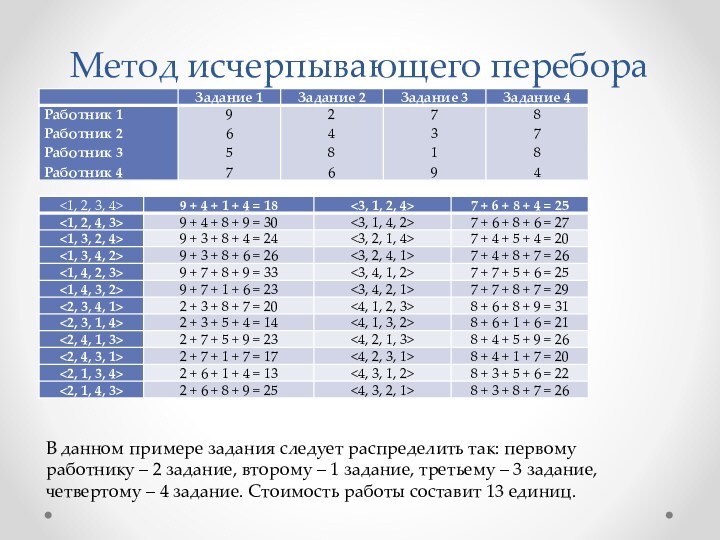
Имеется некоторое число работ и некоторое число исполнителей. Любой исполнитель может быть назначен на выполнение любой (но только одной) работы, но с неодинаковыми затратами. Нужно распределить работы так, чтобы выполнить работы с минимальными затратами.

Если число работ и исполнителей совпадает, то задача называется линейной задачей о назначениях. Обычно, если говорят о задаче о назначениях без дополнительных условий, имеют в виду линейную задачу о назначениях.

матрицей эффективностей A .
( 2

4 1 3 3)
( 1 5 4 1 2 )
A = ( 3 5 2 2 4 )
( 1 4 3 1 4 )
( 3 2 5 3 5 )

РЕШЕНИЕ. Поскольку не указано, будем решать задачу на минимум (стандартная постановка). Решение будем искать венгерским методом.
Составляем исходную таблицу (матрицу):

(выделяем жирным в таблице) и отнимаем от всех элементов

строки. Получим:

Теперь проводим аналогичную процедуру для всех столбцов: ищем наименьший элемент по столбцу и отнимаем его из всех элементов столбца. Получим:

клетки с нулевой стоимостью.

Этап 2. Выбираем строку с одним

нулем (строка №1), выделяем нуль жирным и зачеркиваем (выделено серым) оставшиеся нулевые значения этого столбца (столбца №3).
Выбираем строку с одним нулевым значением (строка №5), выделяем нуль.
Выбираем строку с одним нулем (строка №3), выделяем нуль жирным и зачеркиваем (выделено серым) оставшиеся нулевые значения этого столбца (столбца №4).
Выбираем строку с одним нулем (строка №4), выделяем нуль жирным и зачеркиваем (выделено серым) оставшиеся нулевые значения этого столбца (столбца №1). Выбираем строку с одним нулевым значением (строка №2), выделяем нуль.

Получаем оптимальную матрицу назначений:

Минимальное значение целевой функции: 1+2+2+1+2=8.

Эдмондс (англ.) и Карп (а также Томидзава независимо от

них) показали, что его можно модифицировать так, чтобы достичь времени выполнения O(n^3).

работнику – 2 задание, второму – 1 задание, третьему

– 3 задание, четвертому – 4 задание. Стоимость работы составит 13 единиц.

Метод исчерпывающего перебора