Презентация на тему Задачи на движение по прямой (навстречу и вдогонку)

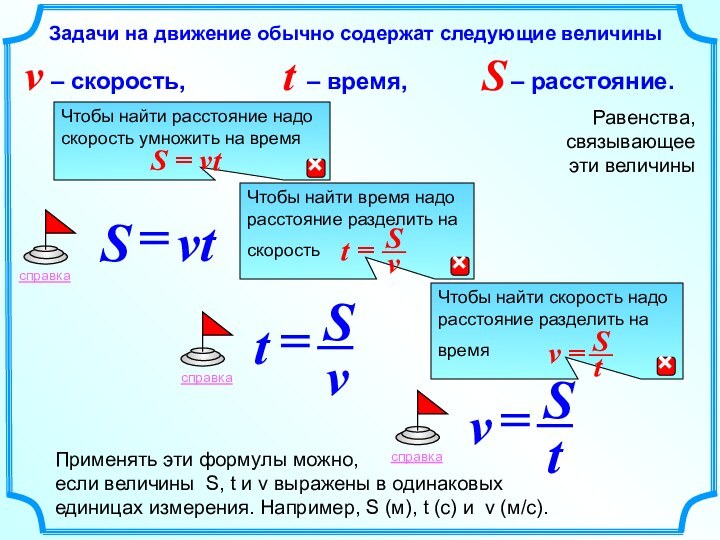
эти величины
Применять эти формулы можно,
если величины S, t

и v выражены в одинаковых
единицах измерения. Например, S (м), t (с) и v (м/с).

справка

справка

справка

v1 + v2

v2 – v1

которыми равно 560 км, навстречу друг другу одновременно выехали

два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 65 км/ч и 75 км/ч?

А

B

1). 65 + 75 = 140(км/ч) скорость навстречу друг другу.

2). 560 : 140 = 4

65 км/ч

75 км/ч

Ответ: 4

одном направлении из одного и того же места на

прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 300 метрам?

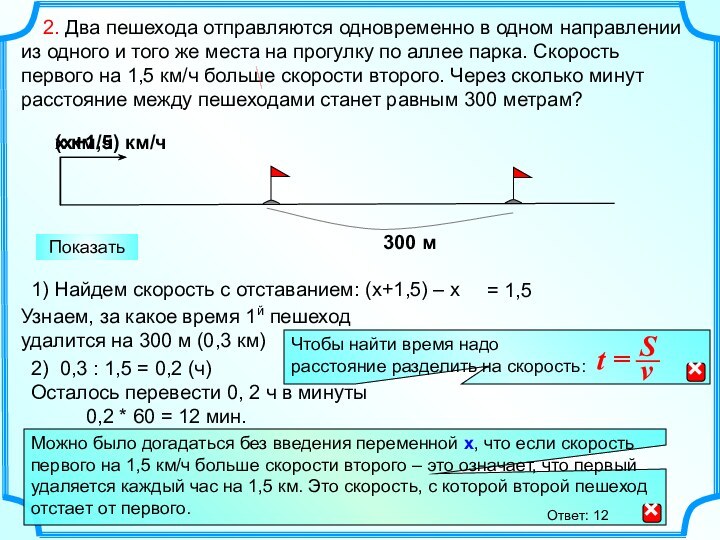
1) Найдем скорость с отставанием: (х+1,5) – х

Узнаем, за какое время 1й пешеход
удалится на 300 м (0,3 км)

2) 0,3 : 1,5 = 0,2 (ч)
Осталось перевести 0, 2 ч в минуты
0,2 * 60 = 12 мин.

Показать

= 1,5

Ответ: 12

расстояние между которыми равно 330 км, навстречу друг другу

одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 180 км от города B. Найдите скорость автомобиля, выехавшего из города A. Ответ дайте в км/ч.

А

B

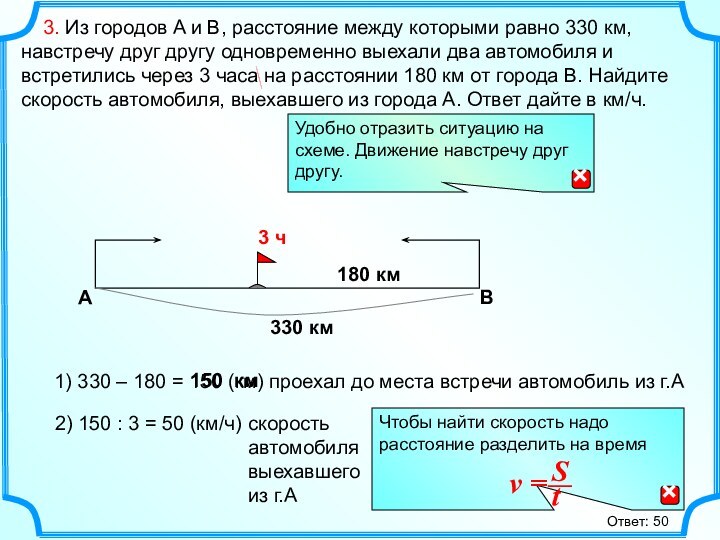
180 км

1) 330 – 180 = 150 (км) проехал до места встречи автомобиль из г.А

скорость
автомобиля
выехавшего
из г.А

150 км

Ответ: 50

2) 150 : 3 = 50 (км/ч)

B равно 435 км. Из города A в город

B со скоростью 60 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города B выехал со скоростью 65 км/ч второй автомобиль. На каком расстоянии от города A автомобили встретятся? Ответ дайте в километрах.

А

1) 435 – 60 = 375 (км) расстояние между автомобилями через 1ч.

2) 60 + 65 = 125 (км/ч) скорость навстречу друг другу

375 км

60 км

3) 375 : 125 = 3 (ч) время встречи

3 ч

4) 60 * 3 = 180 (км) за 3 ч проехал автомобиль из г.А

5) 60 + 180 = 240 (км) расстояние от А до места встречи

Ответ: 240

180 км

B

? км

проехал до встречи 2-й автомобиль.
5. Расстояние между

городами A и B равно 470 км. Из города A в город B выехал первый автомобиль, а через 3 часа после этого навстречу ему из города B выехал со скоростью 60 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 350 км от города A. Ответ дайте в км/ч.

А

B

120 км

2) 120 : 60 = 2 (ч) время, которое проехал до встречи 2-й автомобиль.

3) 350 : (3+2) = 70 (км/ч) скорость 1 автомобиля, который выехал из А и проехал до встречи 350 км, затратив 5ч.

Ответ: 70

2 ч

B одновременно выехали два автомобиля. Первый проехал с постоянной

скоростью весь путь. Второй проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути — со скоростью, на 16 км/ч большей скорости первого, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.

24

x+16

Это условие поможет ввести х …

I половина пути

II половина пути

Решите уравнение самостоятельно и найдите ответ на вопрос задачи.

32 км/ч

B одновременно выехали два автомобиля. Первый проехал с постоянной

скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 16 км/ч, а вторую половину пути — со скоростью 96 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 57 км/ч. Ответ дайте в км/ч.

x-16

96

Это условие поможет ввести х …

I половина пути

II половина пути

Решите уравнение самостоятельно и найдите ответ на вопрос задачи.

64 км/ч

скоростью из города А в город В, расстояние между

которыми равно 72 км. На следующий день он отправился обратно со скоростью на 6 км/ч больше прежней. По дороге он сделал остановку на 6 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.

Путь В-А

х

72

х+6

Решите уравнение самостоятельно и найдите ответ на вопрос задачи.

72

72 км

Это условие поможет ввести х …

6 км/ч

Показать (2)

88-километровый пробег. Первый ехал со скоростью, на 3 км/ч

большей, чем скорость второго, и прибыл к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.

х

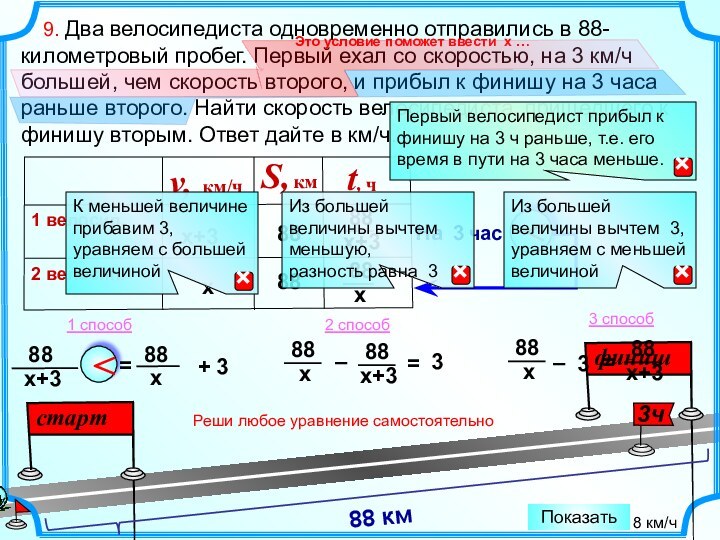
88

88

Это условие поможет ввести х …

Реши любое уравнение самостоятельно

88 км

<

+ 3

=

8 км/ч

Показать

1 способ

2 способ

3 способ

Из пункта А в пункт В, расстояние между которыми

75 км, одновременно выехали автомобилист и велосипедист. Известно, что за час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 6 часов позже автомобилиста. Ответ дайте в км/ч.

х+40

75

Это условие поможет ввести х …

Решите любое уравнение самостоятельно

>

=

10 км/ч

1 способ

2 способ

3 способ

на 750 метров меньше, чем скорый, и на путь

в 180 км тратит времени на 2 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.

Ответ: 45

B равно 150 км. Из города A в город

B выехал автомобиль, а через 30 минут следом за ним со скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах.

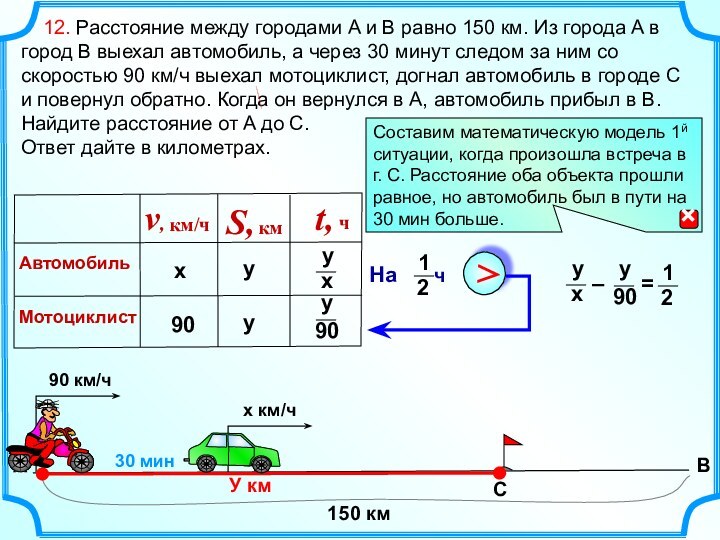
30 мин

А

В

С

Показать (2)

B равно 150 км. Из города A в город

B выехал автомобиль, а через 30 минут следом за ним со скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C.
Ответ дайте в километрах.

30 мин

А

В

С

B равно 150 км. Из города A в город

B выехал автомобиль, а через 30 минут следом за ним со скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C.
Ответ дайте в километрах.

Ответ: 90

А

В

С

=

по шоссе со скоростью 15 км/ч. Через час после

него со скоростью 10 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого  — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч.

х – 10

х – 15

t

= 10

= 30

С системой придется потрудиться. При выборе ответа учтем, что скорость 3-го велосипедиста должна быть больше 15. Ответ: 25.