школьника и инженера
1.Линейка.
2.Циркуль.3.Транспортир.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть













IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
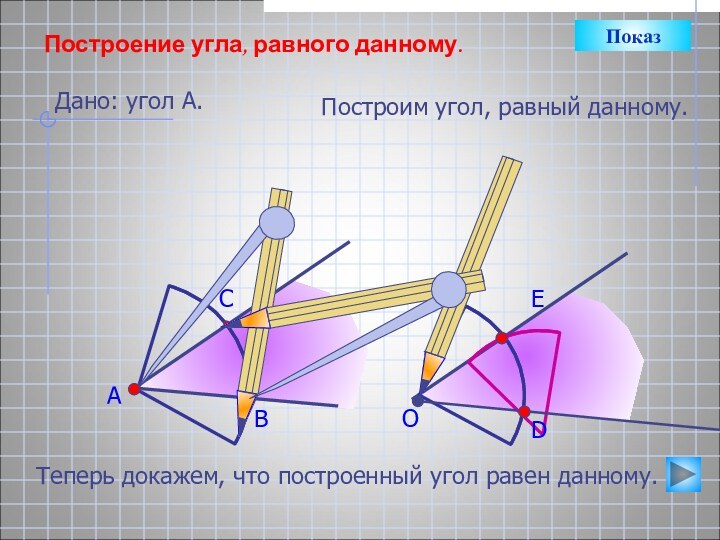
Показ
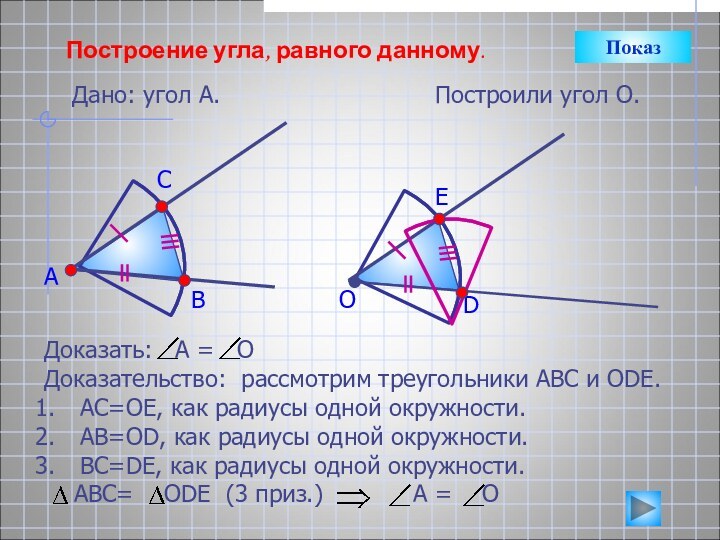
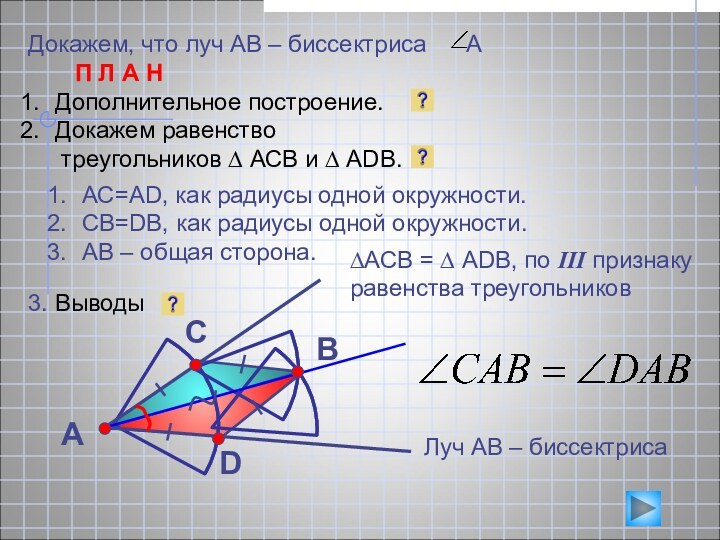
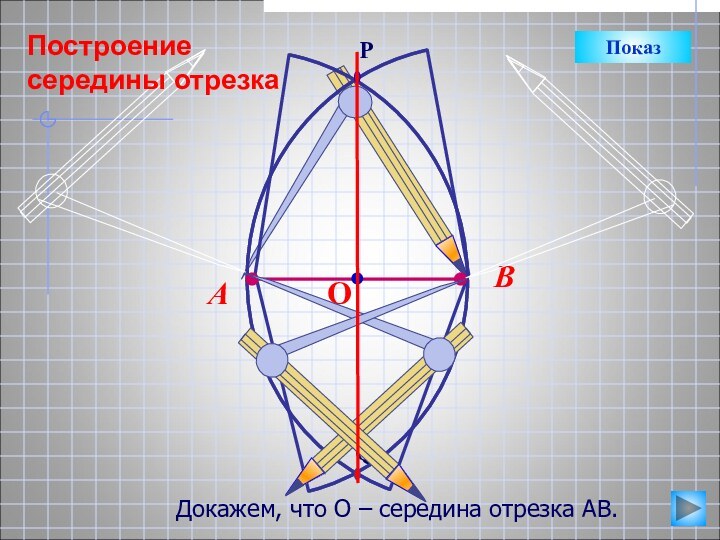
А
В
С
D
АС=АD, как радиусы одной окружности.
СВ=DB, как радиусы одной окружности.
АВ – общая сторона.
?
∆АСВ = ∆ АDВ, по III признаку
равенства треугольников
Луч АВ – биссектриса
?
?
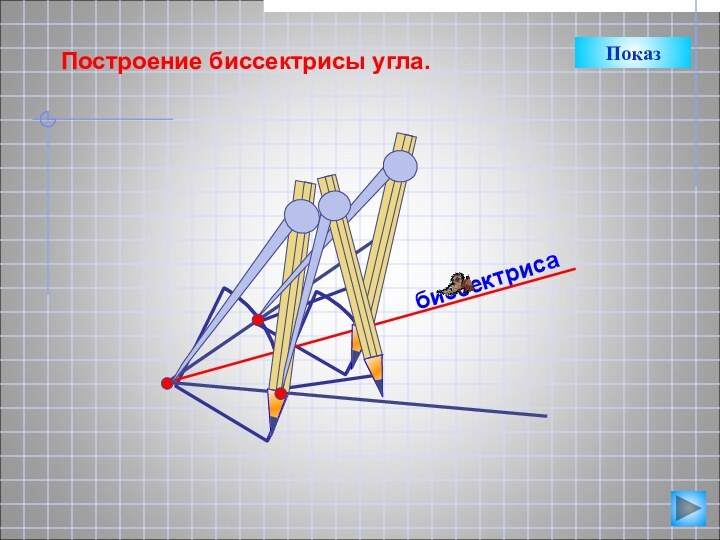
Показ
В
А
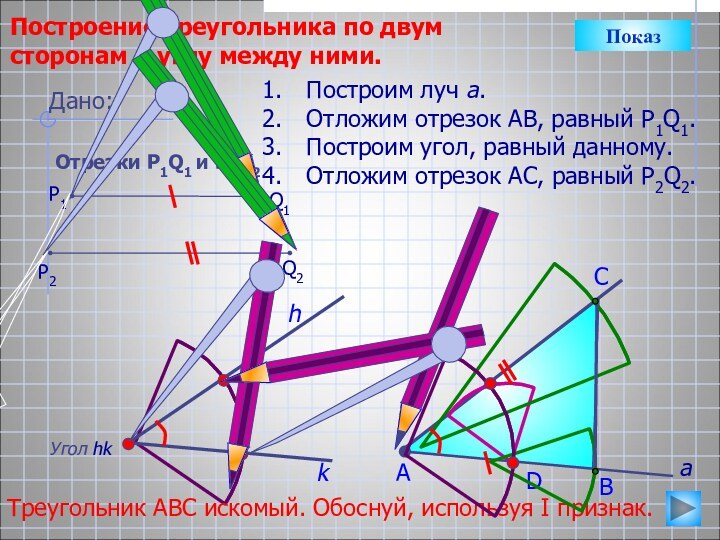
Треугольник АВС искомый. Обоснуй, используя I признак.
Дано:
Отрезки Р1Q1 и Р2Q2
Q1
P1
P2
Q2
а
k
Показ
В
А
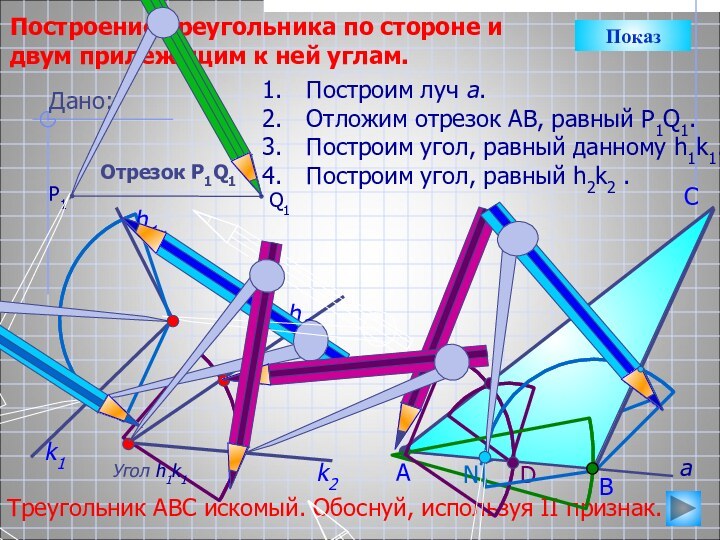
Треугольник АВС искомый. Обоснуй, используя II признак.
Дано:
Отрезок Р1Q1
Q1
P1
а
k2
Показ
h1
k1
N
В
А
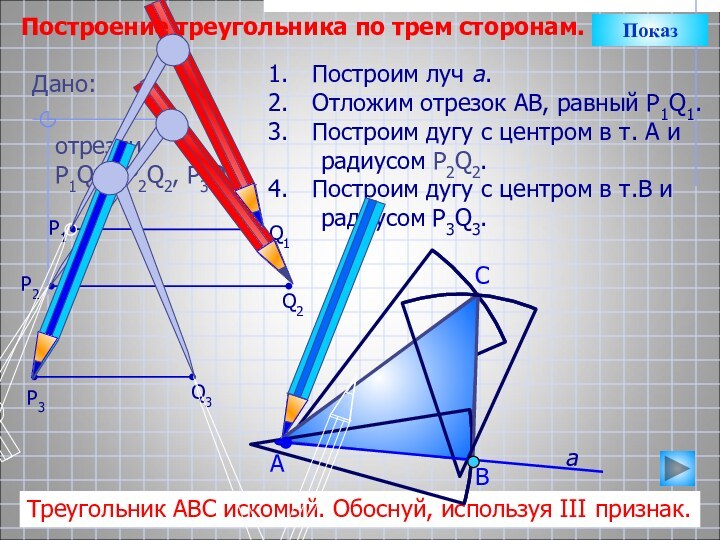
Треугольник АВС искомый. Обоснуй, используя III признак.
Дано:
отрезки
Р1Q1, Р2Q2, P3Q3.
Q1
P1
P3
Q2
а
P2
Q3
Показ
Построение треугольника по трем сторонам.