- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Задачи на смеси, растворы и сплавы
Содержание
- 2. Проблема: задачи на смеси, растворы и сплавы вызывают большие затруднения у выпускников.
- 3. Цель: научится решать задачи на смеси, растворы и сплавы, а также составить дидактический материал.
- 4. Задачи:Собрать теоретический материал.Рассмотреть методы решения задач.Создать дидактический материал.
- 5. Как известно, в основе
- 6. Кроме того, применяются некоторые правила:
- 7. Основные понятия взадачах на смеси,растворы и сплавы
- 8. «Смесь»«Чистое вещество»«Примесь»Доли чистого вещества в смеси –
- 9. Отметим, что 0
- 10. Понятие доли чистого вещества в смеси можно
- 11. Процентное содержание чистого вещества
- 12. При решении задач следует
- 13. Выбор неизвестной (или неизвестных).Выбор чистого вещества.Переход к
- 14. В ходе осуществления этих этапов рекомендую ввести следующую таблицу:
- 15. Задача 1. Морская вода
- 17. Происходит соединение смесей.
- 18. Исходя из третьей строки таблицы, составим уравнение
- 19. Задача 2. Смешали 30%-ный
- 20. Тогда 0,3 x +
- 21. Задача 3. Имеются два
- 22. Решение. Пусть x –
- 24. Становится очевидным,
- 25. Составим уравнение по последней
- 26. Скачать презентацию
- 27. Похожие презентации
Проблема: задачи на смеси, растворы и сплавы вызывают большие затруднения у выпускников.
























Слайд 3
Цель:
научится решать задачи на смеси, растворы и
сплавы, а также составить дидактический материал.
Слайд 4
Задачи:
Собрать теоретический материал.
Рассмотреть методы решения задач.
Создать дидактический материал.
Слайд 5 Как известно, в основе методики
решения этих задач лежит связь между тремя величинами в
виде прямой и обратной зависимостей:
S = VT
T =
-
S
V
V =
-
S
T
A = VT
T =
-
V
A
V
=
A
-
T
- для количества работы А, времени Т и производительности V
- для пути S, времени T и скорости V;
Слайд 6
Кроме того, применяются некоторые правила:
сложение или вычитание скоростей при движении в
движущейся среде, сложение или вычитание производительностей при совместной работе и др.
Слайд 8
«Смесь»
«Чистое вещество»
«Примесь»
Доли чистого вещества в смеси – «a»
Чистое
вещество – «m»
Общее количество – «М»
a =
m : M m = a M M= m : aСлайд 9 Отметим, что 0 ≤
a ≤ 1, ввиду того, что
0 ≤ m ≤ M. Случай a=0 соответствует отсутствию выбранного чистого вещества в рассматриваемой смеси (m=0), случай a =1 соответствует тому, что рассматриваемая смесь состоит только из чистого вещества (m= M).Слайд 10 Понятие доли чистого вещества в смеси можно вводить
следующей условной записью:
Доля чистого
вещества в смеси
=
=
_
Количество чистого вещества в
смесиОбщее количество смеси
Слайд 12 При решении задач следует руководствоваться
тем, что при соединении (разъединении) смесей с одним и
тем же чистым веществом количества чистого вещества и общие количества смесей складываются (вычитаются). Складывать и вычитать доли и процентные содержания нельзя.
Слайд 13
Выбор неизвестной (или неизвестных).
Выбор чистого вещества.
Переход к долям.
Отслеживание
состояния смеси.
Составление уравнения.
Решение уравнения (или их системы).
Формирование ответа.
Основные этапы
решения задачСлайд 15 Задача 1. Морская вода содержит
5% соли по массе. Сколько пресной воды нужно добавить
к 30 кг морской воды, чтобы концентрация составляла 1,5%?Примеры решения задач
Слайд 16
Решение:
Пусть требуется добавить x кг пресной воды.
За чистое вещество
примем соль. Тогда морская вода – это смесь с 5%-ным содержанием чистого вещества, пресная вода – с 0%-ным содержанием чистого вещества.Переходя долям, получаем, что доля соли в морской воде составляет 0,05, доля соли в пресной воде равна 0, доля в смеси, которую нужно получить, – 0,015.
Слайд 18 Исходя из третьей строки таблицы, составим уравнение
m = a M :
0,05 · 30 = 0,015(30 + x).Решим полученное уравнение и находим x = 70.
В данной задаче не содержалось требования найти процентное содержание какого-либо вещества, поэтому нет необходимости переводить доли в процентные содержания.
Ответ: 70 кг.
Слайд 19 Задача 2. Смешали 30%-ный раствор
соляной кислоты с 10%-ным и получили 600 г 15%-ного
раствора. Сколько граммов каждого вещества было взято?Решение: Пусть взяли x г первого раствора, тогда второго раствора (600 – x) г.
Слайд 20 Тогда 0,3 x + 0,1(600
– x) = 0,15 · 600, откуда x =
150, 600 – x = 450.Ответ: 150 г 30%-ного раствора,
450 г 10%-ного раствора.
Слайд 21 Задача 3. Имеются два сплава,
состоящие из цинка, меди и олова. Известно, что первый
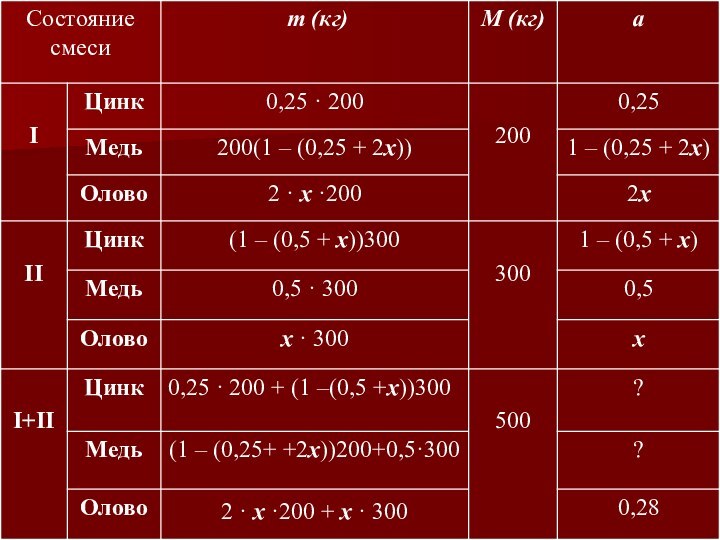
сплав содержит 25% цинка, а второй – 50% меди. Процентное содержание олова в первом сплаве в 2 раза выше, чем во втором. Сплавив 200 кг первого и 300 кг второго, получили новый сплав, в котором оказалось 28% олова. Определить, сколько килограммов меди содержится в получившемся новом сплаве.Пример усложненной задачи
Слайд 22 Решение. Пусть x – доля
олова во II сплаве, тогда 2x – доля олова
в I сплаве. Сначала определим долю олова в данных сплавах. Для этого заполним таблицу, выполнив переход от процентных содержаний к долям.
Слайд 24
Становится очевидным, что
уравнение можно составить по последней строке таблицы, используя зависимость
m = a M :2 · x · 200 + x · 300 = 0,28 · 500, откуда x = 0,2.
Таким образом, доля олова в первом сплаве будет 0,4, а во втором – 0,2.
Теперь выберем в качестве чистого вещества медь, и пусть y – доля меди в получившемся сплаве.
Сосчитаем по таблице долю меди в первом сплаве
1 – (0,25 + 0,4) = 0,35.
Составим таблицу (относительно меди).
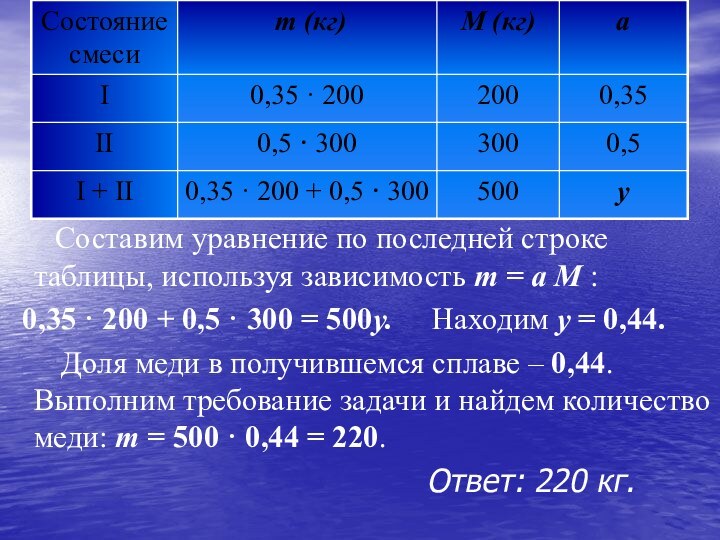
Слайд 25 Составим уравнение по последней строке
таблицы, используя зависимость m = a M :
0,35
· 200 + 0,5 · 300 = 500y. Находим y = 0,44.Доля меди в получившемся сплаве – 0,44. Выполним требование задачи и найдем количество меди: m = 500 · 0,44 = 220.
Ответ: 220 кг.