Слайд 2
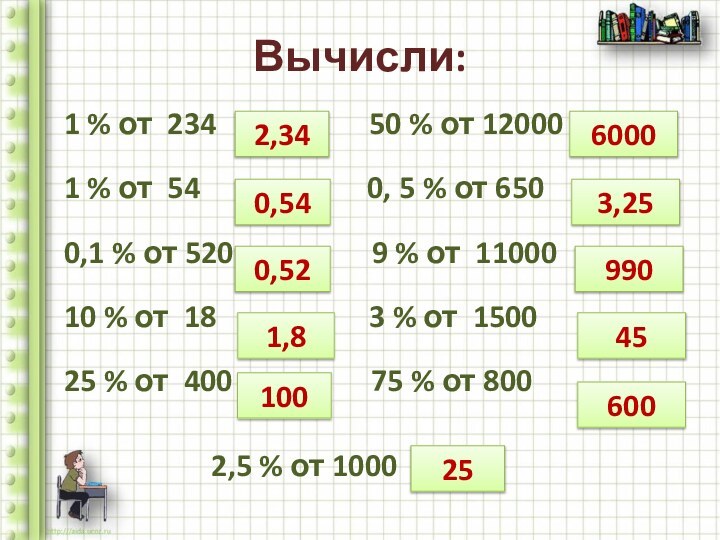
Вычисли:
1 % от 234
50 %
от 12000
1 % от 54 0, 5 % от 650
0,1 % от 520 9 % от 11000
10 % от 18 3 % от 1500
25 % от 400 75 % от 800
2,5 % от 1000
2,34
0,54
0,52
1,8
100
25
6000
3,25
990
45
600
Слайд 3
Найди процентное отношение:
10 по отношению к
10
20 по отношению к 200
12
по отношению к 60
48 по отношению к 16
35 по отношению к 7
100 %
10 %
20 %
300 %
500 %
Слайд 4
Найди число при условии, что
2 % составляют 16 кг
10 %
составляют 350р
4 % составляют 9 м
200 % составляют 32см
0,1 % составляет 55 р
800 кг
3500 р
225 м
16 см
55000 р
Слайд 5
Заполни таблицу
0,5
50 %
1/4
25 %
0,1
10 %
0,2
1/5
0,02
2 %
5 %
1/20
0,01
1/100
Слайд 6
Повтори правила
1. Чтобы найти х процентов
от числа,
нужно умножить это число
на х/ 100.
2. Чтобы найти число, х процентов
от которого равно данному числу,
нужно разделить данное число
на х/100.
(Замечание. х/100 удобно записывать как
десятичную дробь.)
.
Слайд 7
Реши устно
1. Турист прошел 14 км, что
составляет
70 % всего маршрута. Чему равен весь маршрут?
2. В книге 300 страниц. Аня прочитала
20 % книги. Сколько страниц прочитала
Аня ?
3. Рабочий изготовил 60 деталей, что составляет 25% его задания. Сколько
деталей необходимо изготовить?
20 км
60
240
Слайд 8
Думай, рассуждай, решай
1. В магазине цену
на товар снизили с
500 р. до 400 р.
На сколько процентов снижена цена ?
Решение. За 100 % принимаем первоначальную цену 500 р
500 – 400 = 100 (р.) снижена цена товара
( 100 ∙ 100 % ) : 500 = 20 %
Слайд 9
2. Тетрадь стоит 50 рублей. Сколько
тетрадей можно купить на 550 рублей после повышения цены
на 10 % ?
Решение. За 100 % принимаем первоначальную цену
50 рублей.
10 % = 0,1
50 ∙ 0,1 = 5 (р) составляет повышение
50 + 5 = 55 (р) новая цена
550 : 55 = 10 тетрадей можно купить
Слайд 10
3. Фермеры сдали на завод какое-то
количество выращенной малины и черники.
После сушки получилось 6 т сушеной малины и 5 т черники. Малина теряет 75% своего веса, а черника 80 % своего веса. Сколько свежих ягод было сдано на завод?
Слайд 11
Решение
За 100 % примем вес свежей малины.
Потеря веса у малины 75 % , следовательно
6т малины это 25 %.
6 : 0,25 = 24(т) сдано свежей малины.
За 100 % примем вес свежей черники.
Потеря веса у черники 80 % ,следовательно
5 т черники это 20 %.
5 : 0,2 = 25 (т) сдано свежей черники
25 + 24 = 49 (т) сдано свежих ягод.
Слайд 12
4.При выполнении контрольной работы по математике 12
% учеников не выполнили ни одного задания, 32 %
допустили ошибки, а остальные
14 человек решили
задания верно.
Сколько всего
учеников в классе ?
Слайд 13
Решение
За 100 % примем всех учащихся класса.
1. 12% + 32 % = 44 % учащиеся,
не выполнившие ни одного задания и допустившие ошибку.
2. 100 % - 44 % = 56 % учащиеся, решившие задания верно.
3. 14 : 0,56 =25 учащихся в классе.
Слайд 14
5.На заводе были изготовлены легковые и грузовые машины,
причем 35 % всех изготовленных машин – легковые. Определить
общее количество выпущенных машин, если грузовых машин изготовлено на 240 больше , чем легковых.
Слайд 15
Решение
За 100 % примем общее количество изготовленных машин.
1.
100 % - 35 % = 65 % приходится
на грузовые машины.
2. 65 % - 35 % = 30 % - составляют 240 машин
3. 240 : 0,3 = 800 общее количество изготовленных машин.
Слайд 16
6.Древесина только что срубленного дерева содержала 64
% воды. Через неделю количество воды составляло уже 48
% от веса дерева. На сколько при этом уменьшился вес дерева, если только что срубленное дерево весило 7,5 ц ? (ответ дать с точностью до 0,1 ц.)
Слайд 17
Решение
1. 7,5 ∙ 0,64 = 4,8 (ц)-
содержится воды в только что срубленном дереве.
2. 7,5 –
4,8 = 2,7 (ц) – содержится чистой древесины в дереве.
3. 100 % - 48 % = 52 % -приходится на 2,7 ц. через неделю
4. 2,7 : 0,52 ≈ 5,2 (ц) – весит дерево через неделю.
5. 7,5 – 5,2 ≈ 2,3 (ц)- на столько уменьшился вес дерева через неделю.
Слайд 18
Задачи повышенной трудности
1. Вклад , положенный в
сбербанк два года назад, достиг суммы , равной 1312,5
тыс. руб. Каков был первоначальный вклад при 25 % годовых ?
Пусть х (тыс. руб)- первоначальный размер вклада,
тогда х∙0,25 сумма процентов за первый год.
В конце первого года вклад составит х + 0,25х = 1,25х
Сумма процентов за второй год составит 1,25х∙0,25 = 0,3125х.
В конце второго года вклад составит
1,25х + 0,3125х = 1,5625х.
1,5625х = 1312,5
Х = 840 тыс. руб.
Слайд 19
2. 5 литров сливок с содержанием жира
35 % смешали с 4 литрами 20 %- ных
сливок и к смеси добавили
1 литр чистой воды. Какой жирности получилась смесь ?
Слайд 20
Решение
1. 5 ∙ 0,35 = 1,75 (л)
- жира в 5 л сливок.
2. 4 ∙
0,2 = 0,8 (л) – жира в 4 л сливок.
3. 1,75 + 0,8 = 2,25 (л) – жира в смеси.
4. 5 + 4 + 1 = 10 (л) – вес смеси.
5. 2,25 : 10 = 0,255 = 25,5 % - жирность смеси
Слайд 21
3. Слиток сплава серебра и цинка
весом в 3,5 кг содержал 75 % серебра. Его
сплавили с другим слитком и получили слиток массой 10,5 кг, содержание серебра в котором 84 %. Сколько процентов серебра содержалось во втором слитке ?
Слайд 22
Решение
1. 3,5 ∙ 0,75 = 2,66
(кг) – серебра в первом слитке.
2. 10,5∙ 0,84
= 8,82 (кг) – серебра в сплаве.
3. 8,82 – 2,66 = 6,16 (кг) – серебра во втором слитке.
4. 10,5 – 3,5 = 7 (кг) – вес второго слитка.
5. 6,16 : 7 = 0,88 = 88 % серебра содержалось во втором слитке.
Слайд 23
4.Цену товара сперва снизили на 20 %,
затем новую цену снизили еще на 15 %, и
, наконец, после пересчета произвели снижение еще на 10%. На сколько процентов всего снизили первоначальную цену товара ?
Слайд 24
Решение
1. Пусть первоначальная цена товара х рублей,
что соответствует 100 %.
2. Тогда после первого снижения цена
товара будет х – 0,2х= 0,8х (р.)
3. После второго снижения
0,8х – 0,25∙ 0,8х = 0,68 х (р.)
4. После третьего снижения
0,68х – 0,68х∙ 0,2 = 0,612х (р.)
5. Всего цена товара снизилась на
х – 0,612х = 0,388х
( 0,388х : х) ∙100 = 38,8 %.