- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Площадь плоских фигур
Содержание
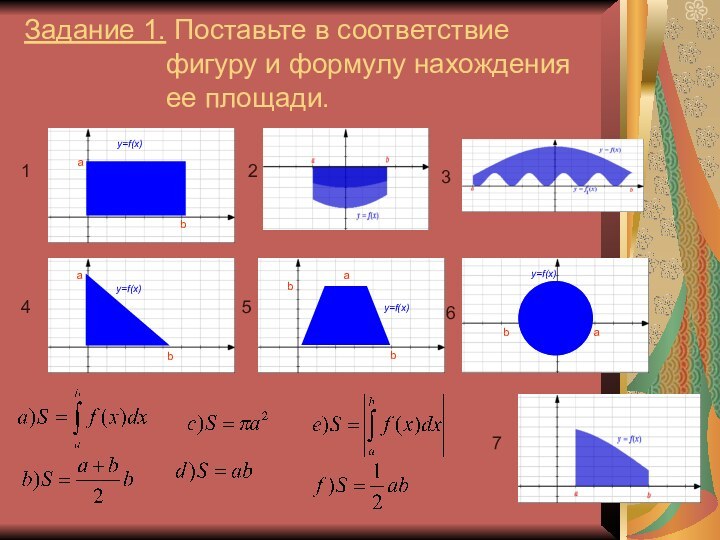
- 2. Задание 1. Поставьте в соответствие фигуру и формулу нахождения ее площади.1234567
- 3. Правильные ответы к заданию 1.1-d2-e3-нет формулы4-f5-b6-c7-a
- 4. Задание 2. По известным формулам попробуйте вычислить площади фигур, закрашенных синим цветом.123
- 5. Задание 3. Что общего в нахождении площадей
- 6. Задание 4. Алгоритм нахождения площади плоских фигур
- 7. Пример. Вычислите площадь фигуры, ограниченной прямой y=x-2
- 8. Пример. Вычислите площадь фигуры, ограниченной прямой y=x-2
- 9. Пример. Вычислите площадь фигуры, ограниченной прямой y=x-2 и параболой y=x2- 4x+2.Применить формулу вычисления площади
- 10. Итог урокаКак найти площади изображенных фигур?Ответ:Ответ:
- 11. Итог урокаКак найти площади изображенных фигур?Ответ:Ответ:
- 12. Скачать презентацию
- 13. Похожие презентации
Задание 1. Поставьте в соответствие фигуру и формулу нахождения ее площади.1234567


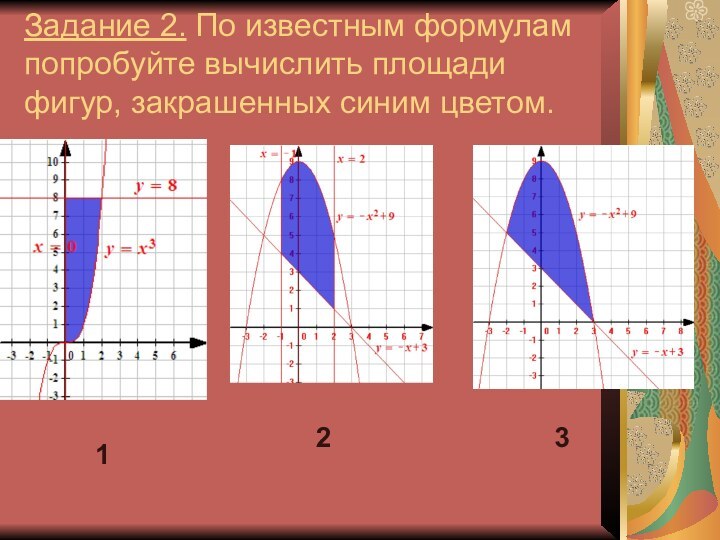






Слайд 4 Задание 2. По известным формулам попробуйте вычислить площади
фигур, закрашенных синим цветом.
1
2
3
Слайд 5 Задание 3. Что общего в нахождении площадей фигур
задания 2?
Правильный ответ
Площадь S фигуры, ограниченной прямыми x=a, x=b
и графиками функций y=f(x), y=g(x), непрерывных на отрезке [a;b] и таких, что для всех х из отрезка [a;b] выполняется неравенство g(x)≤f(x), вычисляется по формулеСлайд 6 Задание 4. Алгоритм нахождения площади плоских фигур более
сложного вида с помощью определенного интеграла
Графически построить фигуру,
ограниченную заданными функциямиОпределить прямые x=a и x=b, которые ограничивают данную фигуру (если не заданы, то найти абсциссы точек пересечения графиков функций)
Определить график какой функции на отрезке [a;b] выше – это и будет функция y=f(x), а другая у=g(x)
Применить формулу вычисления площади
Слайд 7 Пример. Вычислите площадь фигуры, ограниченной прямой y=x-2 и
параболой
y=x2- 4x+2.
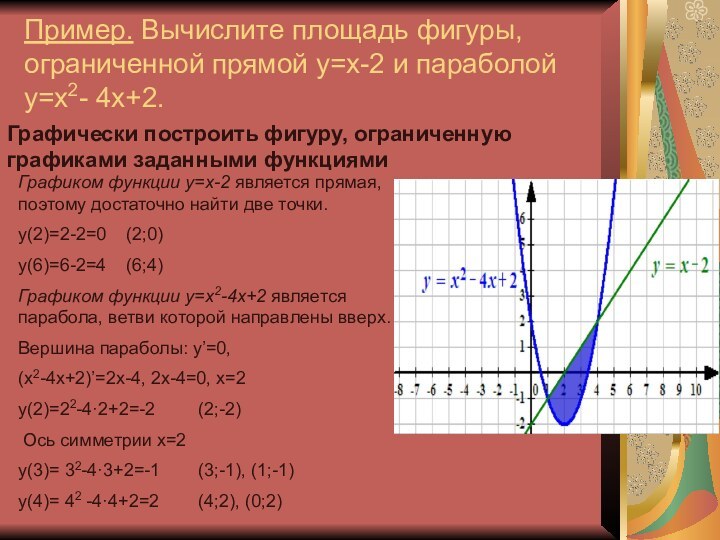
Графически построить фигуру, ограниченную графиками заданными функциями
Графиком
функции y=x-2 является прямая, поэтому достаточно найти две точки.у(2)=2-2=0 (2;0)
у(6)=6-2=4 (6;4)
Графиком функции y=x2-4x+2 является парабола, ветви которой направлены вверх.
Вершина параболы: у’=0,
(x2-4x+2)’=2х-4, 2х-4=0, х=2
у(2)=22-4·2+2=-2 (2;-2)
Ось симметрии х=2
у(3)= 32-4·3+2=-1 (3;-1), (1;-1)
у(4)= 42 -4·4+2=2 (4;2), (0;2)
Слайд 8 Пример. Вычислите площадь фигуры, ограниченной прямой y=x-2 и
параболой
y=x2- 4x+2.
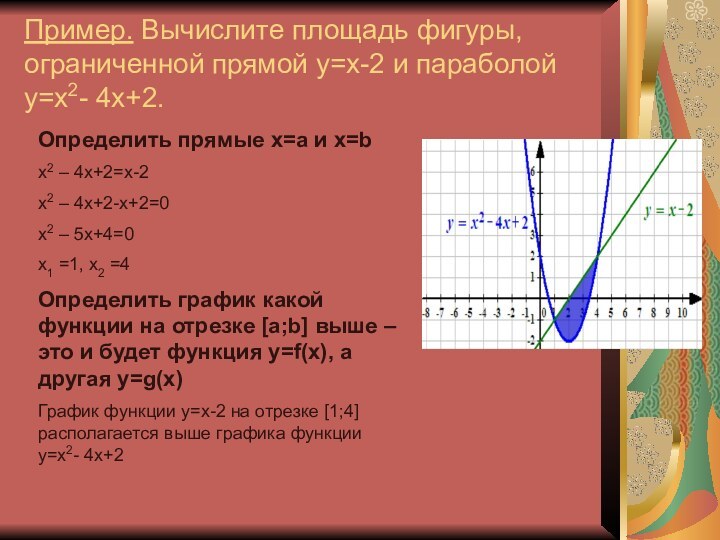
Определить прямые x=a и x=b
х2 – 4х+2=х-2
х2
– 4х+2-х+2=0х2 – 5х+4=0
х1 =1, х2 =4
Определить график какой функции на отрезке [a;b] выше – это и будет функция y=f(x), а другая у=g(x)
График функции у=х-2 на отрезке [1;4] располагается выше графика функции y=x2- 4x+2