- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Задания с производной при подготовке к ЕГЭ Задания В8 и В14
Содержание
- 2. Типы заданийГеометрический смысл производнойКасательная в точкеМеханический смысл производнойПромежутки возрастания-убыванияЛокальные экстремумыНаибольшие/наименьшие значения на отрезке
- 3. Геометрический смысл производной (теория)Следующие величины равныЗначение производной
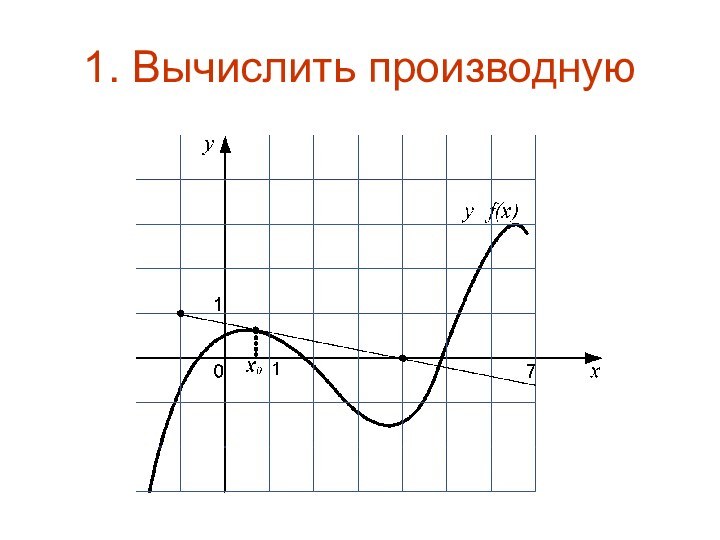
- 4. 1. Вычислить производную
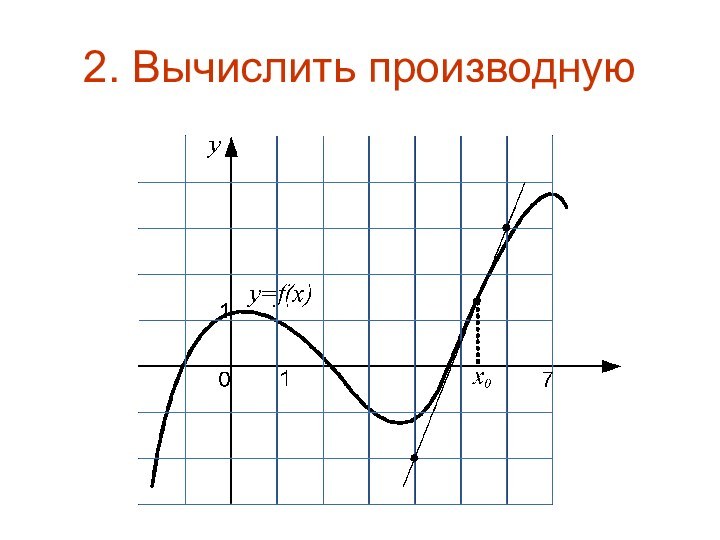
- 5. 2. Вычислить производную
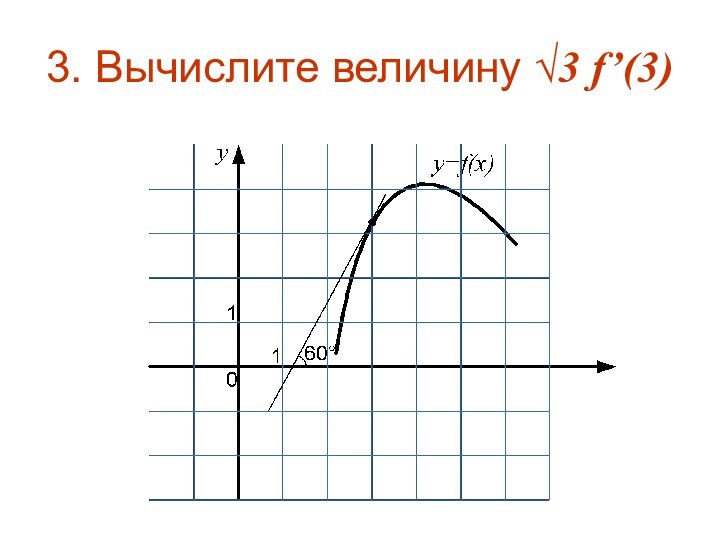
- 6. 3. Вычислите величину √3 f’(3)
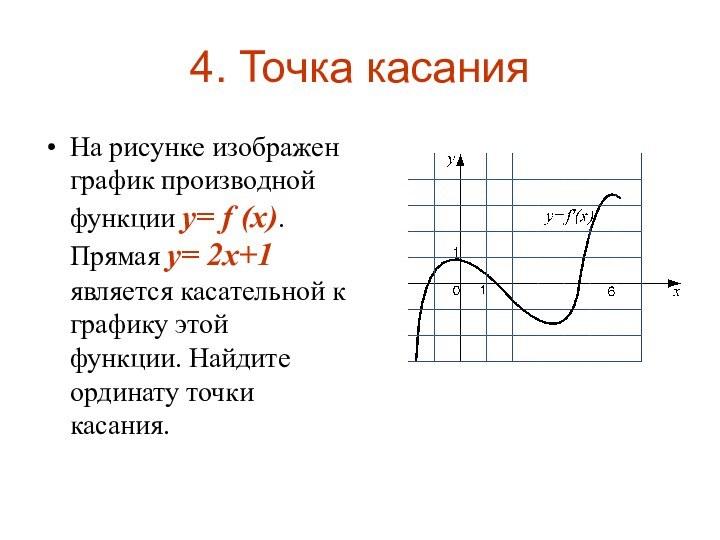
- 7. 4. Точка касанияНа рисунке изображен график производной
- 8. 5. Точка касанияНа рисунке изображен график производной
- 9. Задачи 6-8Касательная к графику функции y= 3
- 10. Задачи 9 - 12Прямая y= x+2 является
- 11. Механический смысл производнойЕсли s(t) – функция, задающая
- 12. Движение материальной точкиМатериальная точка движется прямолинейно по
- 13. Промежутки возрастания-убыванияОпределение возрастающей (убывающей) функции на промежуткеФункция
- 14. Возрастание/убываниеНа рисунке изображен график функции y=f(x). Определите
- 15. Возрастание/убываниеНа рисунке изображен график функции y=f(x). Определите
- 16. Возрастание/убываниеНа рисунке изображен график функции y=f(x). Определите,
- 17. Возрастание/убываниеНа рисунке изображен график производной функции y=f(x).
- 18. Возрастание/убываниеНа рисунке изображен график производной функции y=f(x).
- 19. Возрастание/убываниеНайдите количество промежутков убывания функции y=f(x), если
- 20. Локальные экстремумыОпределение максимума (минимума) функцииТочка х0 является
- 21. Локальный экстремумНа рисунке изображен график производной функции
- 22. Локальный экстремумНа рисунке изображен график производной функции
- 23. Локальный экстремумНа рисунке изображен график производной функции
- 24. Локальный экстремумНа рисунке изображен график производной функции
- 25. Локальный экстремумНайдите количество точек максимума функции y=f(x),
- 26. Экстремумы на отрезкеНаибольшее значение функции на отрезке
- 27. Экстремумы на отрезкеНайдите точку, в которой функция
- 28. Скачать презентацию
- 29. Похожие презентации
Типы заданийГеометрический смысл производнойКасательная в точкеМеханический смысл производнойПромежутки возрастания-убыванияЛокальные экстремумыНаибольшие/наименьшие значения на отрезке














Слайд 2
Типы заданий
Геометрический смысл производной
Касательная в точке
Механический смысл производной
Промежутки
возрастания-убывания
Слайд 3
Геометрический смысл производной (теория)
Следующие величины равны
Значение производной f’(x0)
в точке x0
Тангенс угла наклона касательной к графику функции
y= f (x0) в точке x0 Угловой коэффициент касательной к графику функции y= f (x0) в точке x0
Слайд 7
4. Точка касания
На рисунке изображен график производной функции
y= f (x). Прямая y= 2x+1 является касательной к
графику этой функции. Найдите ординату точки касания.
Слайд 8
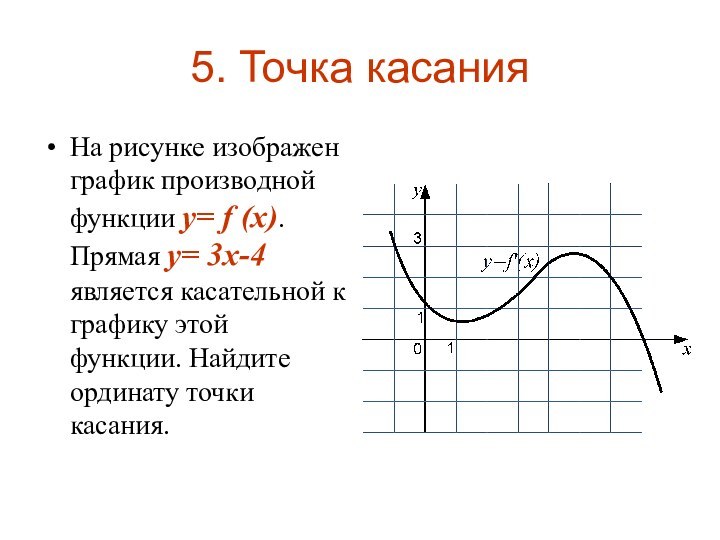
5. Точка касания
На рисунке изображен график производной функции
y= f (x). Прямая y= 3x-4 является касательной к
графику этой функции. Найдите ординату точки касания.
Слайд 9
Задачи 6-8
Касательная к графику функции y= 3 –
2x – x2 параллельна прямой y= 4x. Найдите абсциссу
точки касания.Касательная к графику функции y= 3 – 2x – x2 проходит через точки А(1, 1) и В(-1, 5). Найдите абсциссу точки касания
Найдите положительное значение параметра b, при котором прямая y= -3 является касательной к графику функции y= 2x2 + bx – 1.
Слайд 10
Задачи 9 - 12
Прямая y= x+2 является касательной
к графику функции y= аx2 – х + 6
. Найдите а.Прямая y= 2x является касательной к графику функции y= - x2 +7х + с . Найдите с.
Прямая y= kx + b является касательной к графику функции y= - x2 +4х - 1 в точке А(1,2). Найдите b.
Касательная к графику функции y= x(x-2) проходит через точки А(1, -2) и В(-3, 6). Найдите ординату точки касания
Слайд 11
Механический смысл производной
Если s(t) – функция, задающая закон
движения материальной точки (пройденный путь в зависимости от времени),
то v(t)=s’(t) – мгновенная скорость точки
Слайд 12
Движение материальной точки
Материальная точка движется прямолинейно по закону
s(t)=1/3 t3 + ½ t2 – 9t +1, где
s – расстояние от точки отсчета в метрах, а t – время в секундах с начала движения. Через сколько секунд после начала движения скорость точки будет равна 3 м/с?Материальная точка движется прямолинейно по закону s(t)=6 + 2t – 0,25t2, где s – расстояние от точки отсчета в метрах, а t – время в секундах с начала движения. Через сколько секунд после начала движения точка остановится?
Материальная точка движется прямолинейно по закону s(t)= 4 + 2t – t2, где s – расстояние от точки отсчета в метрах, а t – время в секундах с начала движения. Какова была начальная скорость точки (в м/с)?
Слайд 13
Промежутки возрастания-убывания
Определение возрастающей (убывающей) функции на промежутке
Функция является
возрастающей на промежутке ↔ когда ее производная положительна в
любой точке промежуткаФункция является убывающей на промежутке ↔ когда ее производная отрицательна в любой точке промежутка
Слайд 14
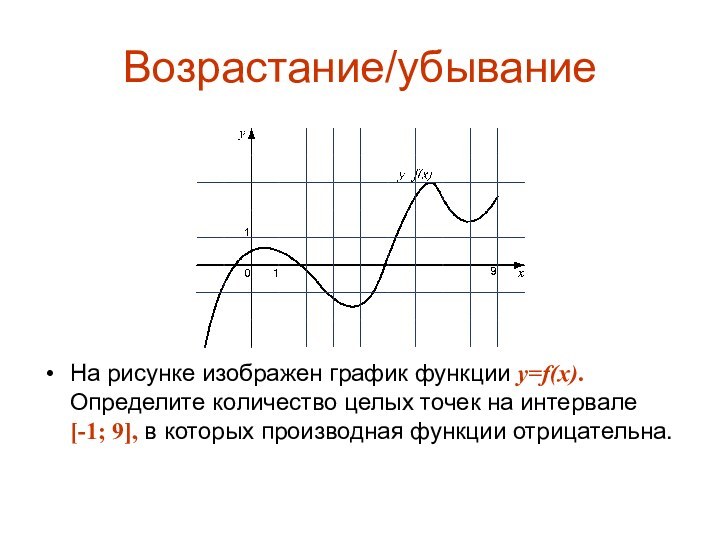
Возрастание/убывание
На рисунке изображен график функции y=f(x). Определите количество
целых точек на интервале [-1; 9], в которых производная
функции отрицательна.
Слайд 15
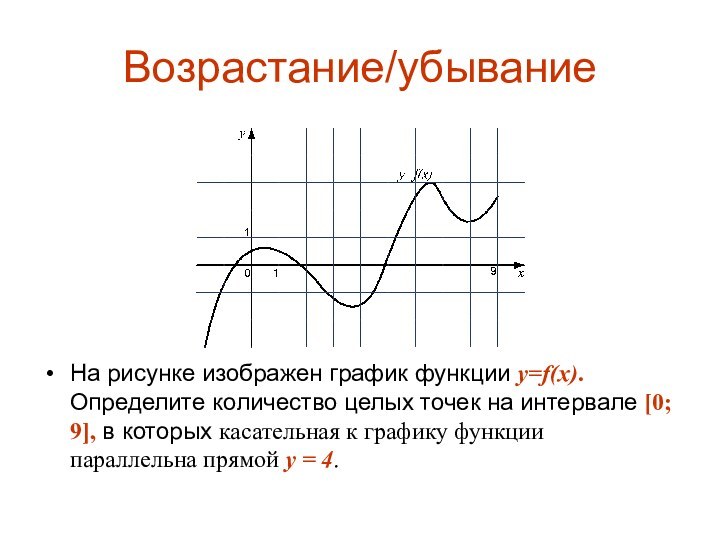
Возрастание/убывание
На рисунке изображен график функции y=f(x). Определите количество
целых точек на интервале [0; 9], в которых касательная
к графику функции параллельна прямой y = 4.
Слайд 16
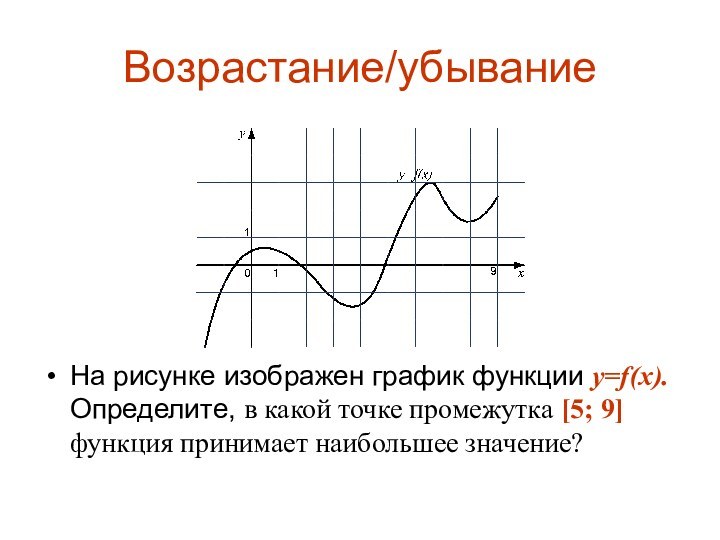
Возрастание/убывание
На рисунке изображен график функции y=f(x). Определите, в
какой точке промежутка [5; 9] функция принимает наибольшее значение?
Слайд 17
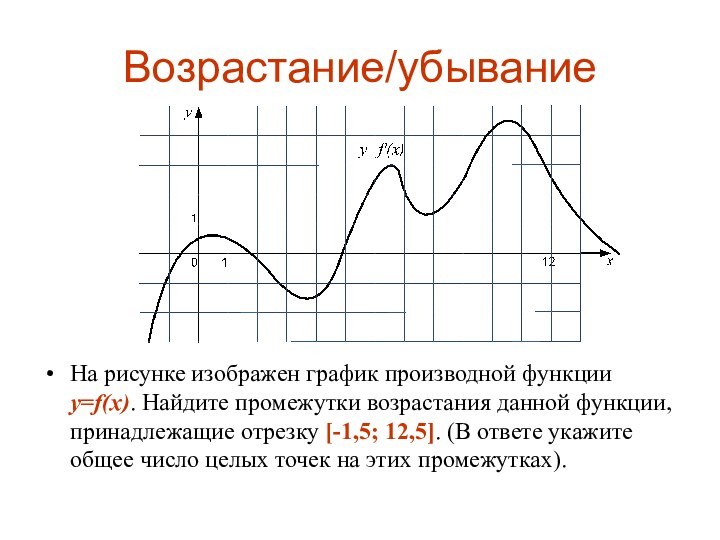
Возрастание/убывание
На рисунке изображен график производной функции y=f(x). Найдите
промежутки возрастания данной функции, принадлежащие отрезку [-1,5; 12,5]. (В
ответе укажите общее число целых точек на этих промежутках).
Слайд 18
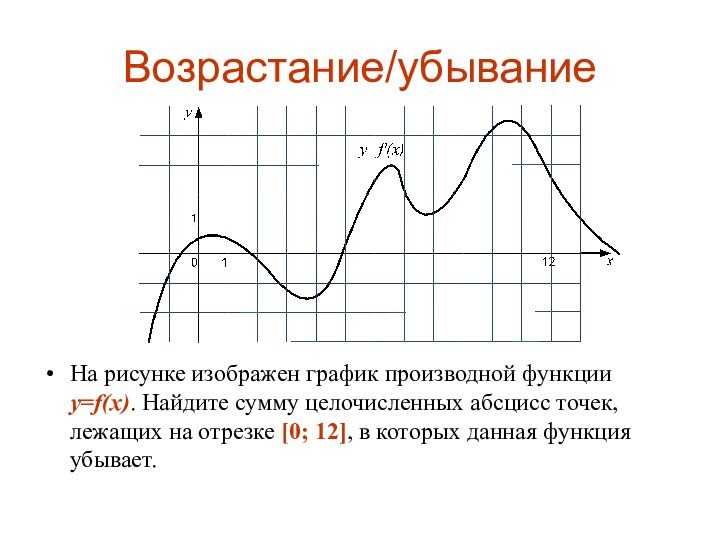
Возрастание/убывание
На рисунке изображен график производной функции y=f(x). Найдите
сумму целочисленных абсцисс точек, лежащих на отрезке [0; 12],
в которых данная функция убывает.
Слайд 19
Возрастание/убывание
Найдите количество промежутков убывания функции y=f(x), если ее
производная имеет вид f’(x) = (x2 – 1)(x2 –
9)(x – 4)2
Слайд 20
Локальные экстремумы
Определение максимума (минимума) функции
Точка х0 является точкой
максимума функции y=f(x) , если f’(x0)=0 и при переходе
через эту точку производная меняет знак с плюса на минус.Точка х0 является точкой минимума функции y=f(x) , если f’(x0)=0 и при переходе через эту точку производная меняет знак с минуса на плюс.
Слайд 21
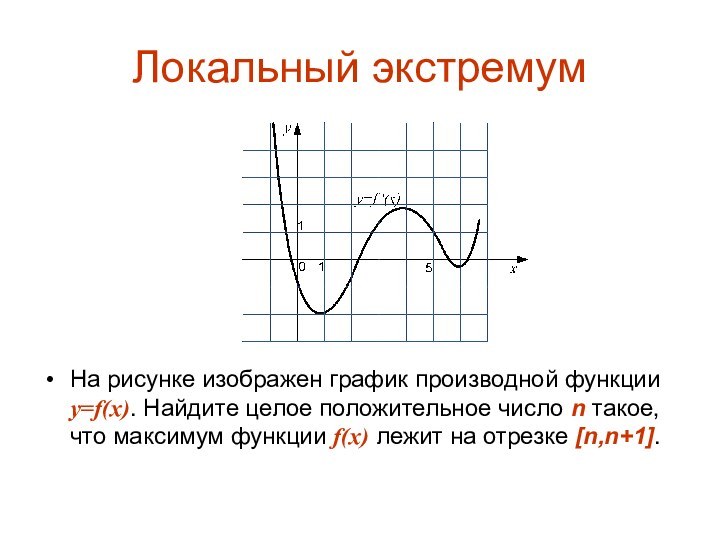
Локальный экстремум
На рисунке изображен график производной функции y=f(x).
Найдите целое положительное число n такое, что максимум функции
f(x) лежит на отрезке [n,n+1].
Слайд 22
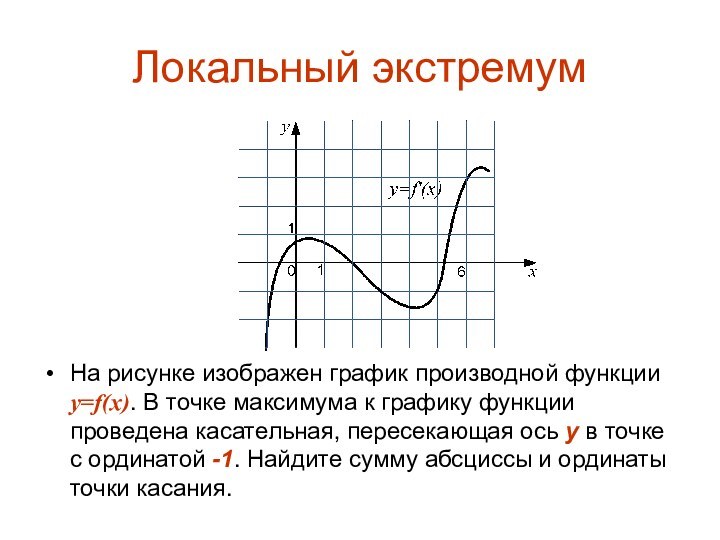
Локальный экстремум
На рисунке изображен график производной функции y=f(x).
В точке максимума к графику функции проведена касательная, пересекающая
ось у в точке с ординатой -1. Найдите сумму абсциссы и ординаты точки касания.
Слайд 23
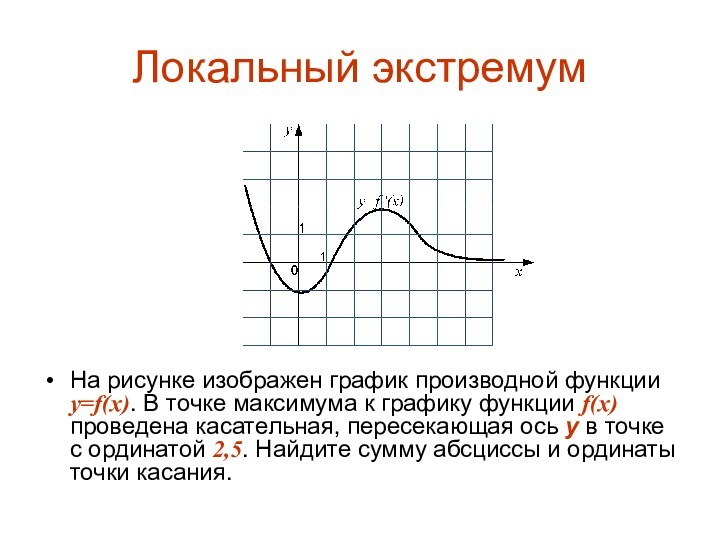
Локальный экстремум
На рисунке изображен график производной функции y=f(x).
В точке максимума к графику функции f(x) проведена касательная,
пересекающая ось у в точке с ординатой 2,5. Найдите сумму абсциссы и ординаты точки касания.
Слайд 24
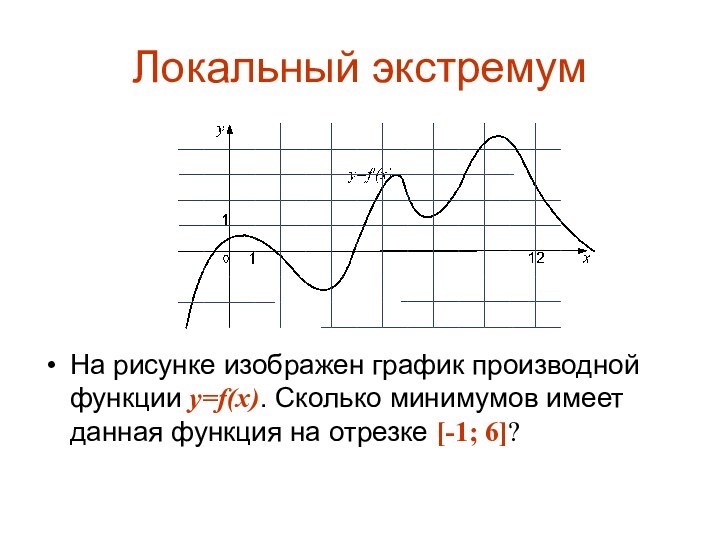
Локальный экстремум
На рисунке изображен график производной функции y=f(x).
Сколько минимумов имеет данная функция на отрезке [-1; 6]?
Слайд 25
Локальный экстремум
Найдите количество точек максимума функции y=f(x), если
f’(x) = (x2 + 3x – 4)(x2 – 16)(x2
– 1)
Слайд 26
Экстремумы на отрезке
Наибольшее значение функции на отрезке находится
как наибольшее из локальных максимумов и значений на границах
Наименьшее
значение функции на отрезке находится как наименьшее из локальных минимумов и значений на границах
Слайд 27
Экстремумы на отрезке
Найдите точку, в которой функция
y=2x3
+ 9x2 – 60x +1 принимает наибольшее значение на
промежутке [-6; 6].Найдите значение функции y=1/4x4 - 2x2 +5 в точке максимума
Найдите наименьшее значение функции y=π/√3 - √3 x – 2 cosx + 11 на отрезке [0; π/2]





























