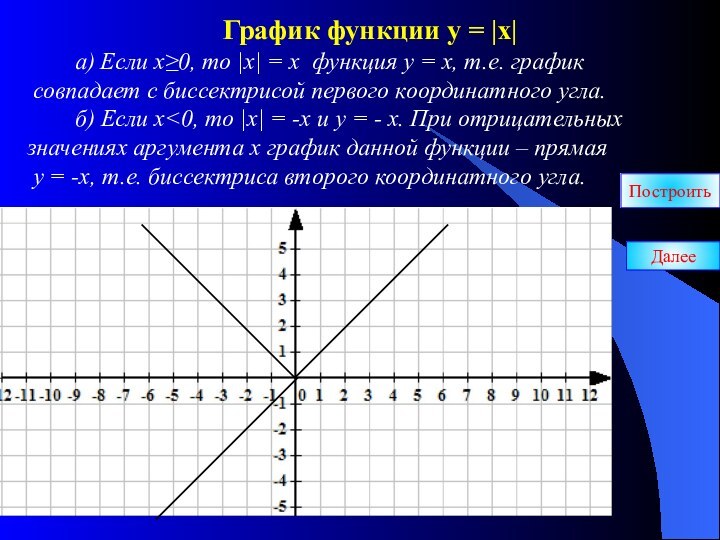
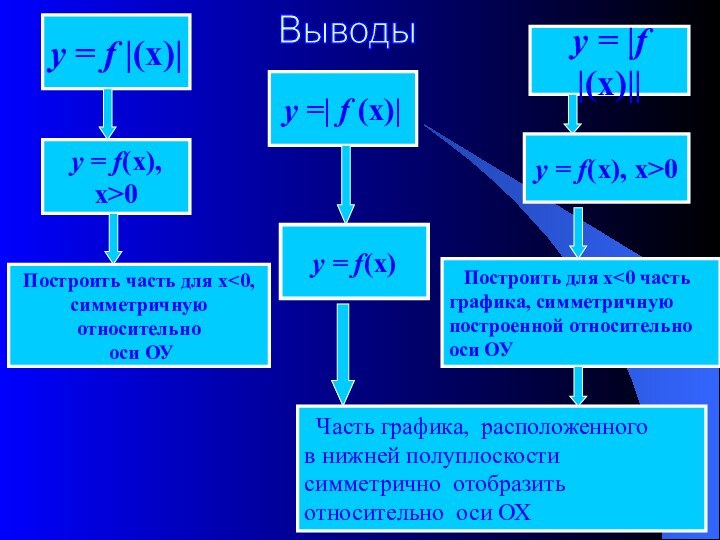
= f |(х)|:
1.Построить график функции у
= f(х) для х>0;
2.Построить для х<0 часть графика, симметричную построенной относительно оси ОУ.
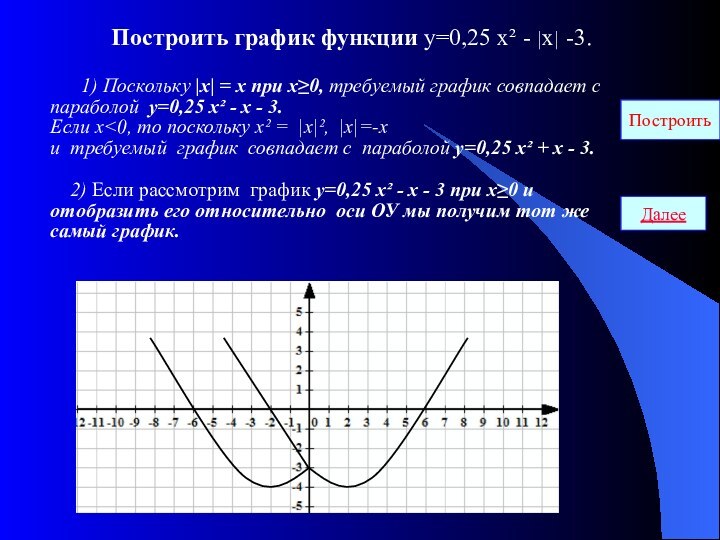
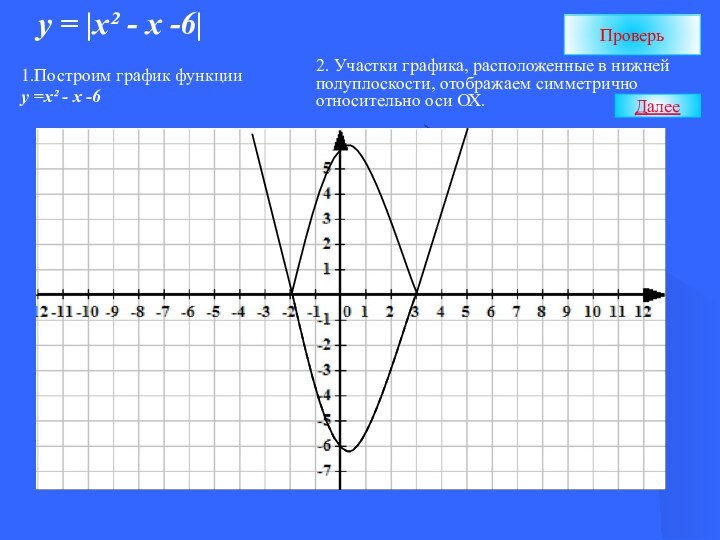
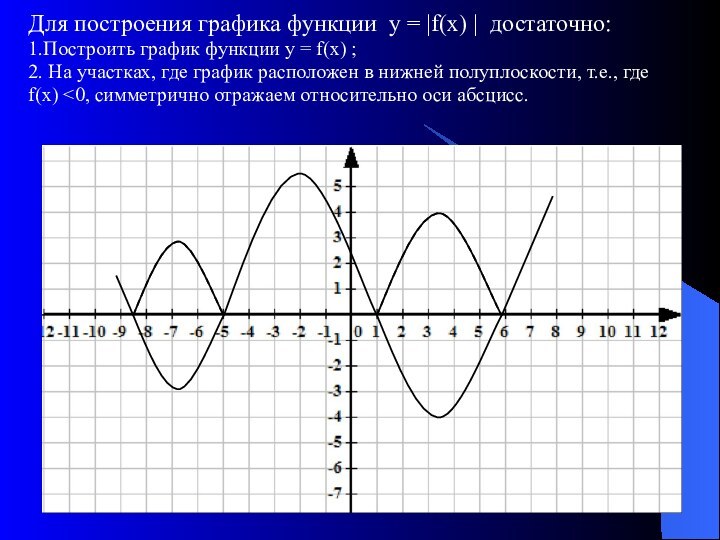
Для построения графика функции у = | f(х) |
1.Построить график функции у = f(х) ;
2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х) <0, строить кривые, симметричные построенным графикам относительно оси абсцисс.
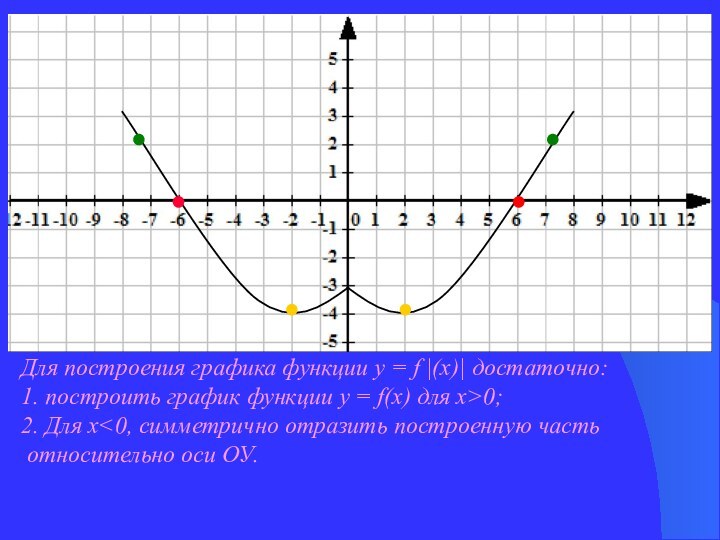
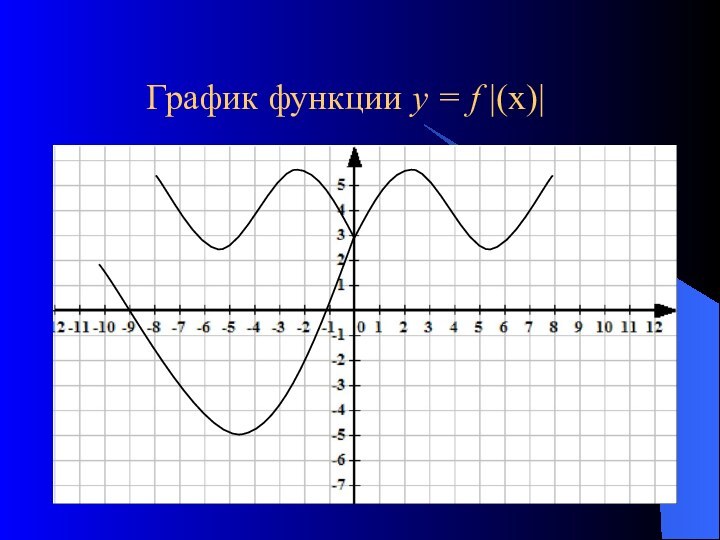
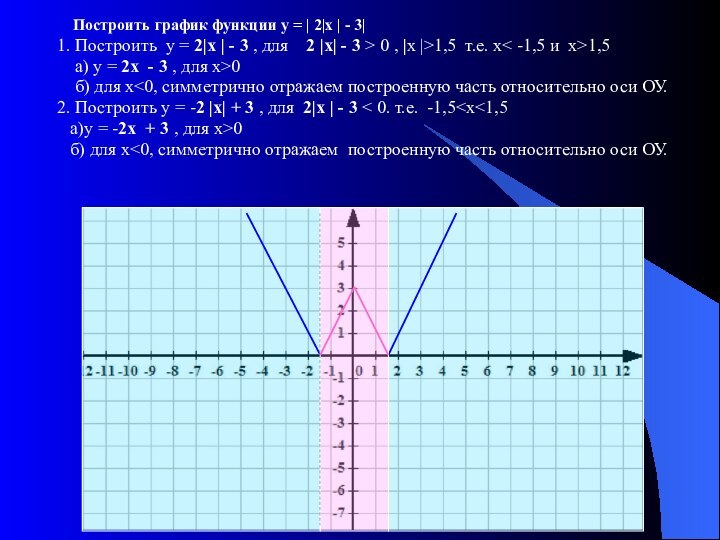
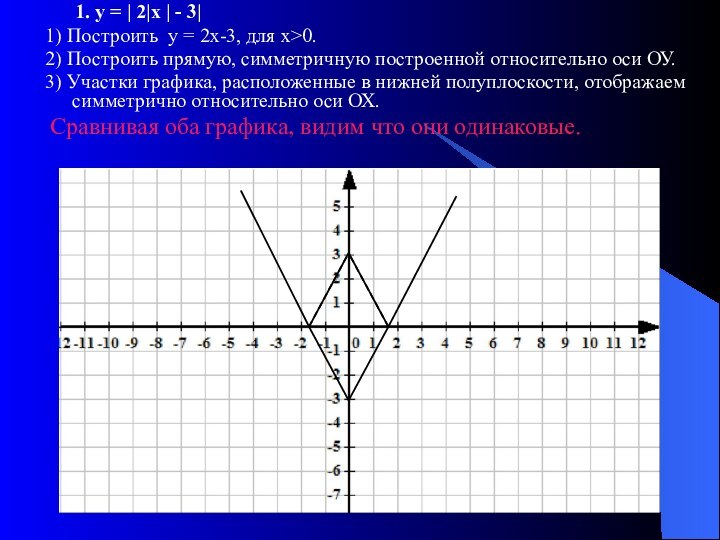
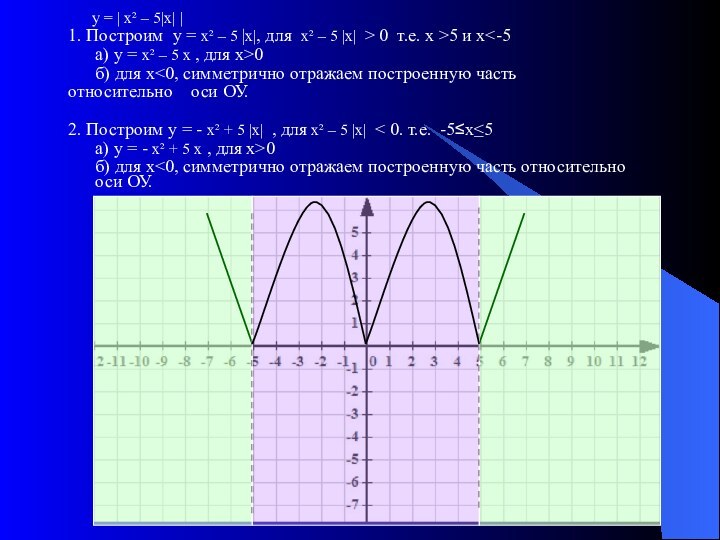
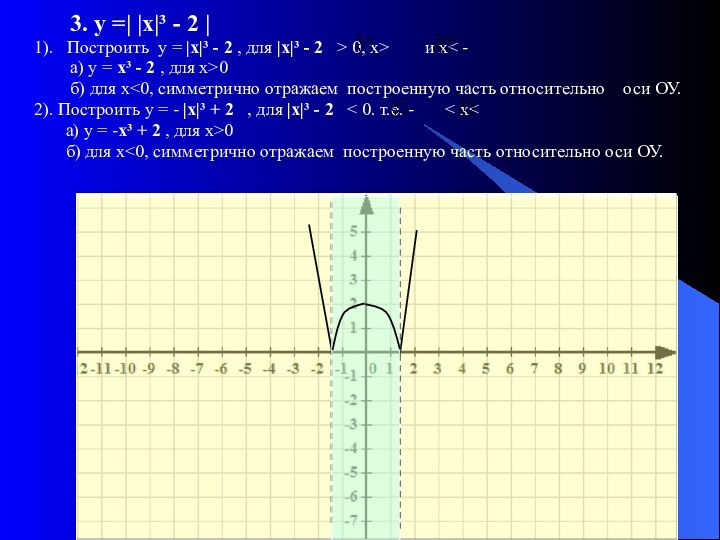
Для построения графика функции у = | f |(х)| |
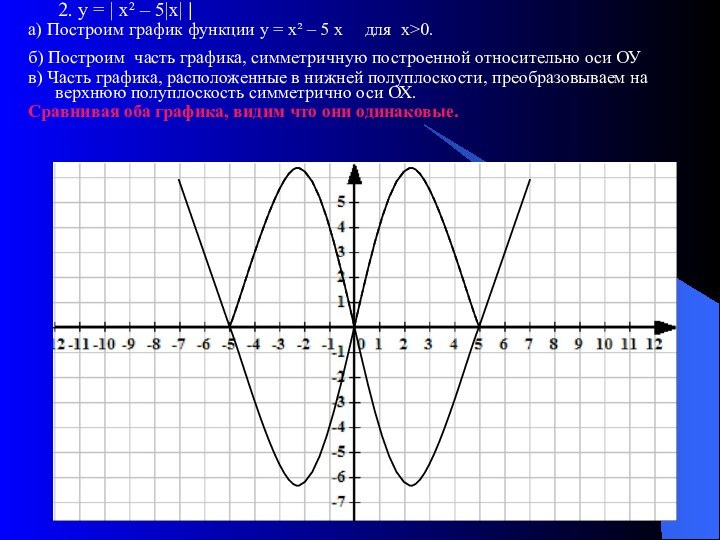
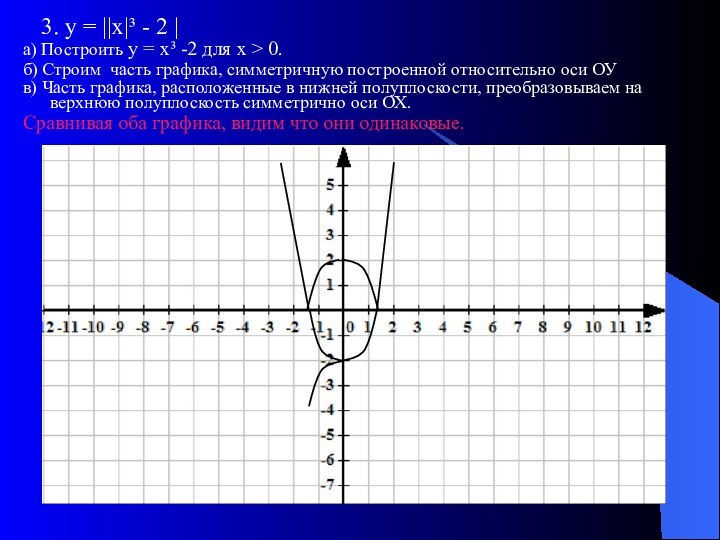
1. Построить график функции у = f(х) для х>0.
2. Строим вторую часть графика, т. е. построенный график симметрично отражаем относительно ОУ
3. Участки получившегося графика, расположенные в нижней полуплоскости, преобразовываем на верхнюю полуплоскость симметрично оси ОХ.
Выводы