Слайд 2
Цель работы
исследование зависимости между радиусом, длиной окружности и
площадью круга.
Задачи:
Систематизировать теоретические сведения о круге и окружности в школьном курсе математики.
Исследовать изменение длины окружности и площади круга в зависимости от изменения длины радиуса.
Изучить историю вопроса.
Показать применение материалов исследований при решении задач, в том числе задач с практическим содержанием, математических парадоксов.
Слайд 3
Методы
Работа с учебной и научно-популярной литературой.
Социологический опрос:
82человека;
33ученика 9-10кл.;
33родителя; 16 учителей.
Наблюдение, сравнение, анализ, аналогия.
Доказательство выдвинутых
гипотез.
Решение задач нестандартными способами.
Слайд 4
Актуальность.
Практическая
направленность.
Богатая история вопроса.
Продолжение предыдущих исследований.
Слайд 5
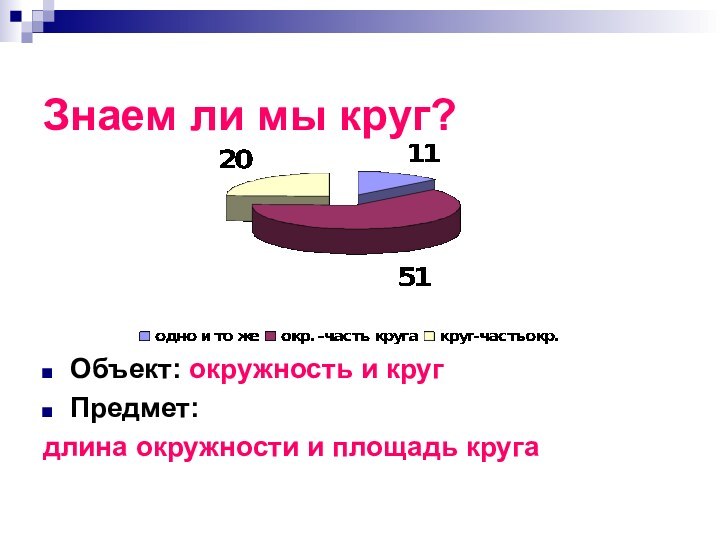
Знаем ли мы круг?
Объект: окружность и круг
Предмет:
длина
окружности и площадь круга
Слайд 6
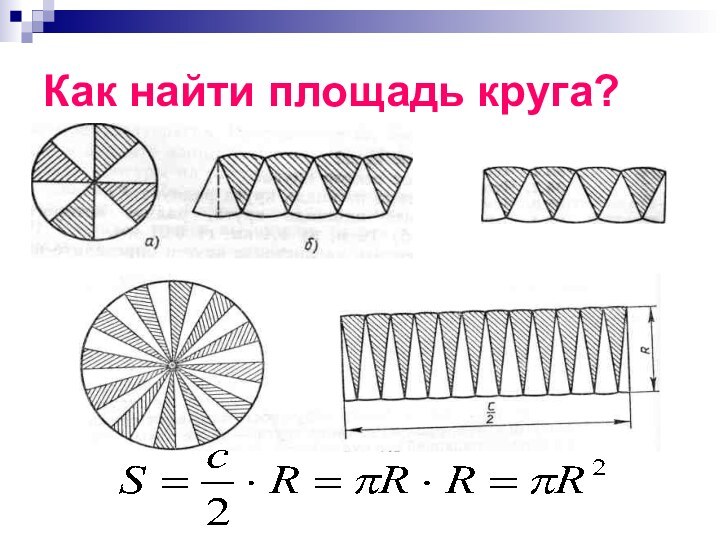
Теоретические сведения
Окружность
Слайд 8
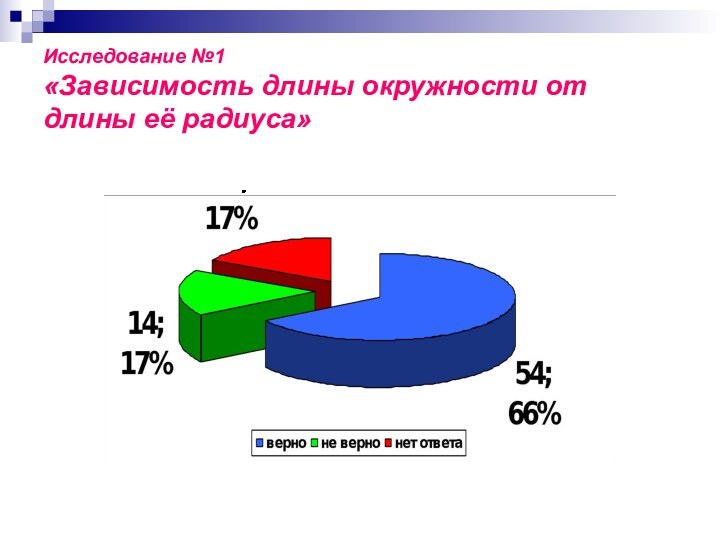
Исследование №1
«Зависимость длины окружности от длины её радиуса»
Слайд 9
Исследование №1
«Зависимость длины окружности от длины её радиуса»
при изменении (увеличении или уменьшении) радиуса окружности в
раз её длина изменяется (увеличивается или уменьшается)
также в раз.
длина окружности пропорциональна её радиусу.
Слайд 10
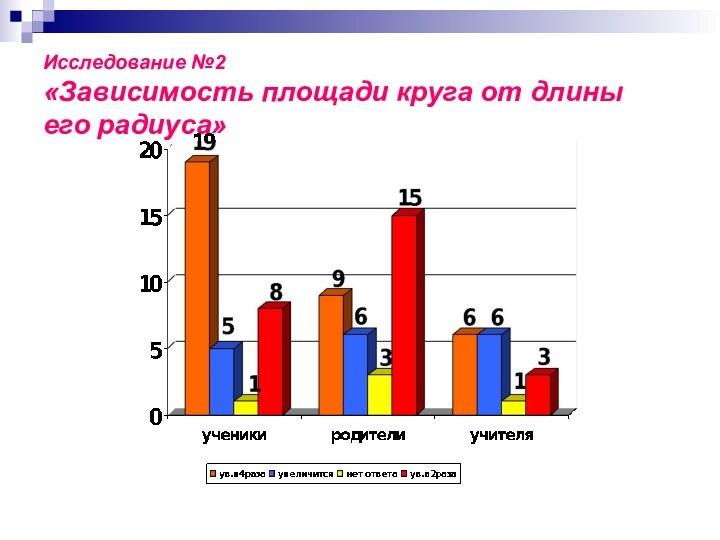
Исследование №2
«Зависимость площади круга от длины его радиуса»
Слайд 11
Исследование №2
«Зависимость площади круга от длины его радиуса»
при изменении (увеличении или уменьшении) радиуса круга в
раз его площадь изменяется (увеличивается или уменьшается) в раз.
площадь круга пропорциональна квадрату его радиуса.
раз.
Слайд 12
Исследование №3
«Максимальная площадь при заданном периметре»
При заданном периметре
круг ограничивает большую площадь, чем квадрат.
При заданном периметре именно
круг ограничивает максимальную площадь по сравнению с любыми другими фигурами.
Слайд 13
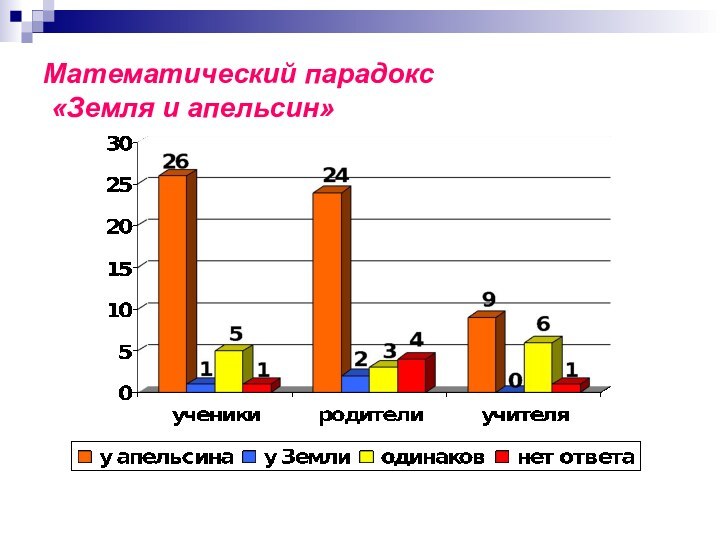
Математический парадокс
«Земля и апельсин»
Слайд 14
Исследование №4
«Изменение радиуса при изменении длины окружности»
Расстояние между концентрическими окружностями зависит только от разности длин
этих окружностей (а) и не зависит от длины радиуса (R)
Слайд 15
Решение задач 5-6класс
Задача №1 (№866,Виленкин)
Длина окружности 1,2 м.
Чему равна длина другой окружности, у которой диаметр в
2 раза больше диаметра первой окружности?
Ответ:2,4метра (Смотри исследование №1!)
Задача №2(№867,Виленкин)
Найдите площадь круга, у которого радиус 8 см. Найдите площадь второго круга, у которого радиус составляет радиуса первого круга.
Ответ:48см2; 36см2 (Смотри исследование №2!)
Задача №3 «Две клумбы» (№95.8, учебник-собеседник)
Отец Вали и Веры предложил девочкам сделать две клумбы. Он дал им верёвку длиной 6м, чтобы с её помощью наметить границу каждой клумбы. Валя решила сделать клумбу квадратной, а Вера – круглой. Чья клумба будет иметь большую площадь? Радиус круглой клумбы вычислите с точностью до сотых. Во сколько раз площадь одной клумбы будет больше площади другой?
Ответ: площадь круглой клумбы будет примерно в 1, 28 раза больше, чем квадратной (радиус 0,96м) (Смотри исследование №3!)
Слайд 16
Решение задач 9класса, из дополнительной литературы
Задача №1
№1102(Атанасян)
Как изменится
длина окружности, если радиус окружности:
а)увеличить в 3 раза; б)уменьшить
в 2 раза; в) увеличить в раз; г) уменьшить в раз?
Ответ: увеличится в 3 раза, уменьшится в 2 раза, увеличится в раз; уменьшится в раз (смотри исследование №1).
Задача №2 «Земной шар и мышь»
Если обтянуть земной шар по экватору проволокой и затем прибавить к её длине 1м, то сможет ли между проволокой и землёй проскочить мышь?
Ответ: да
Решение.
Обычно отвечают, что промежуток будет тоньше волоса: что значит прибавка в один метр по сравнению с 40 миллионами метров земного экватора! В действительности же величина промежутка равна . Не только мышь, но и крупный кот проскочит в такой промежуток!!! (смотри исследование №4).
Слайд 17
История числа «ПИ»
3,141592653589793238462643383279…
Это я знаю и
помню прекрасно:
"Пи" многие знаки мне лишни, напрасны.
Нужно только постараться
И запомнить все, как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Слайд 18
Архимед
Уж, пыль клубится над дорогой,
То в
рабство путь, в ярмо цепей.
«Убей меня, но лишь не
трогай,
О, варвар, этих чертежей!»
Прошли столетий вереницы,
Научный подвиг не забыт.
Никто не знает, кто убийца,
Но знают все,
кто был убит!
Слайд 19
Квадратура круга – синоним неразрешимости
1.Квадратура круга
2.Трисекция угла
3.Удвоение куба.