Презентация на тему Золотое сечение

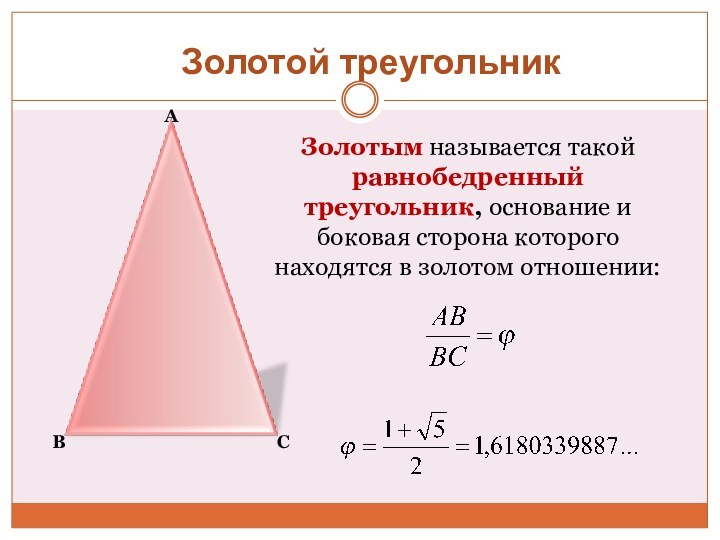
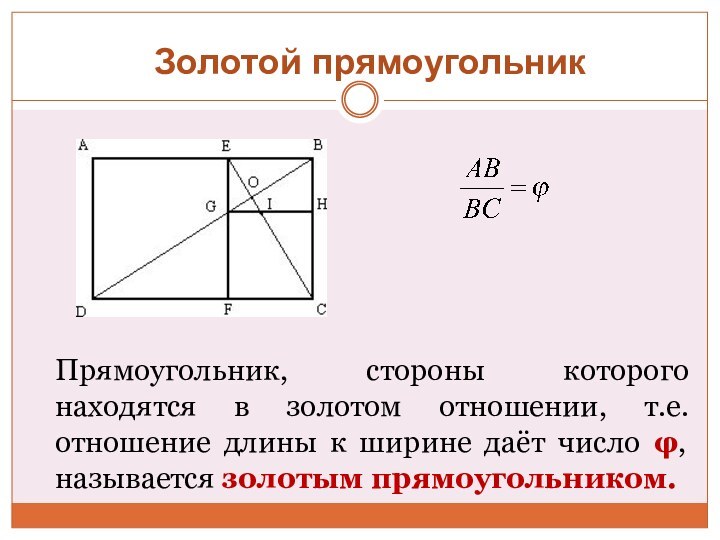
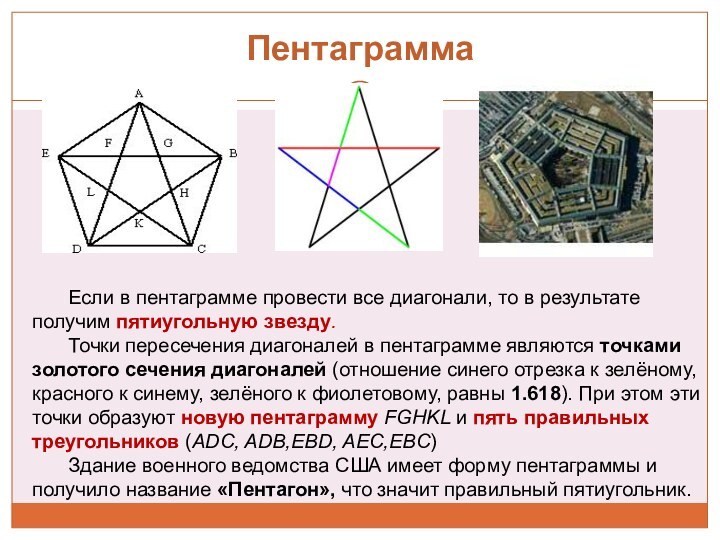
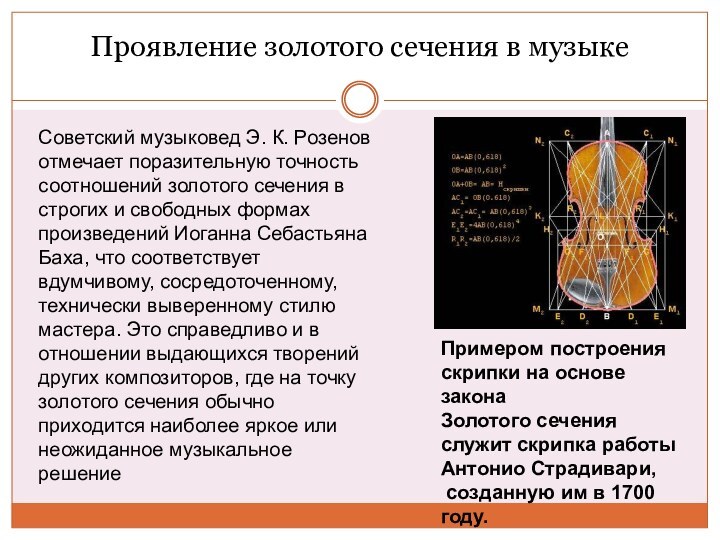
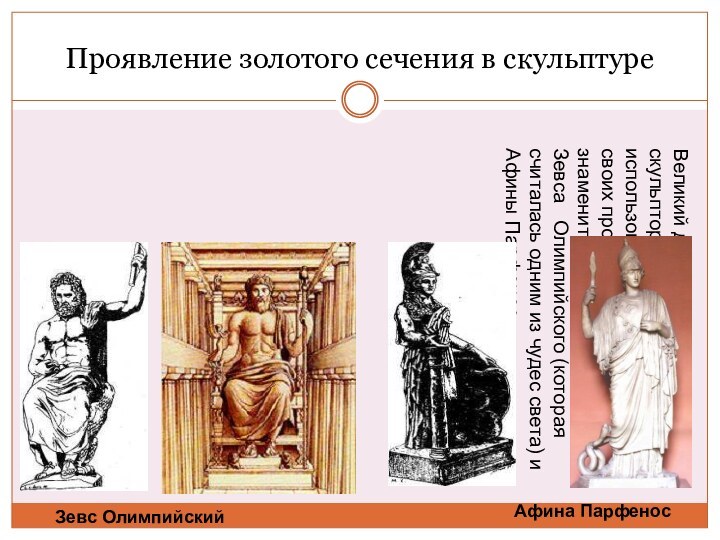
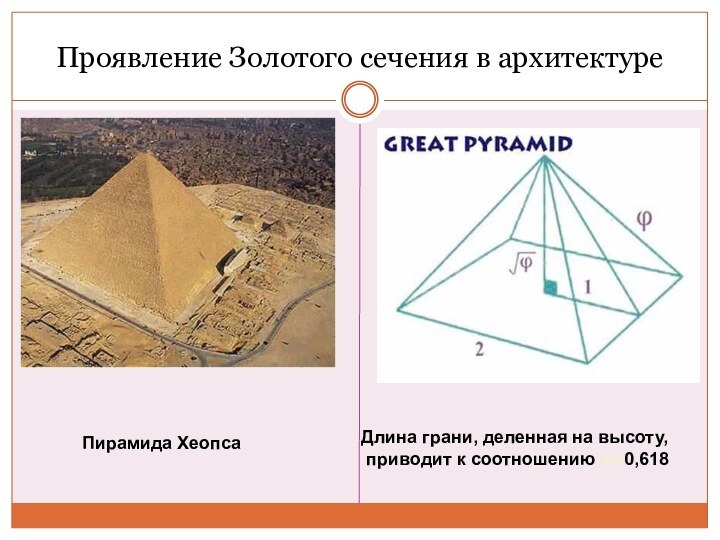
c или с : b

= b : а

Золотое сечение - меньшая часть так относится к большей, как большая ко всему целому.

Приблизительная его величина – 1,6180339887.

В округленном процентном значении пропорции частей целого будут соотноситься как 62% к 38%.
Это соотношение действует в формах пространства и времени.

золотом сечении отражение космического порядка, а Иоганн Кеплер называл

его одним из сокровищ геометрии. Современная наука рассматривает золотое сечение как «ассиметричную симметрию», называя его в широком смысле универсальным правилом отражающим структуру и порядок нашего мироустройства.

о пропорциях–одно из величайших достижений греческой математики.

Термин «золотое сечение»

ввёл Леонардо да Винчи.

Евдокс (408 – ок.355 г.г.до н.э.)

Пифагор (580-500 г.г.до н.э.)

Леонардо да Винчи (1452-1519 г.г.)

Представление о золотых пропорциях имели древние египтяне, знали о них и на Руси, но впервые научно золотое сечение объяснил монах Лука Пачоли в книге «Божественная пропорция» (1509), иллюстрации к которой предположительно сделал Леонардо да Винчи. Пачоли усматривал в золотом сечении божественное триединство: малый отрезок олицетворял Сына, большой – Отца, а целое – Святой дух.

сечения связано имя итальянского математика Леонардо Фибоначчи. В результате

решения одной из задач ученый вышел на последовательность чисел, известную сейчас как ряд Фибоначчи: 0,1,1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. На отношение этой последовательности к золотой пропорции обратил внимание Кеплер: «Устроена она так, что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности». Сейчас ряд Фибоначчи это арифметическая основа для расчетов пропорций золотого сечения во всех его проявлениях.

сторона которого находятся в золотом отношении:

Золотой треугольник

отношение длины к ширине даёт число φ, называется золотым

прямоугольником.

Золотой прямоугольник

результате получим пятиугольную звезду.
Точки пересечения диагоналей в пентаграмме

являются точками золотого сечения диагоналей (отношение синего отрезка к зелёному, красного к синему, зелёного к фиолетовому, равны 1.618). При этом эти точки образуют новую пентаграмму FGHKL и пять правильных треугольников (ADC, ADB,EBD, AEC,EBC)
Здание военного ведомства США имеет форму пентаграммы и получило название «Пентагон», что значит правильный пятиугольник.

золотое сечение можно без труда обнаружить в природе. Так,

под него попадают соотношение хвоста и тела ящерицы, расстояния между листьями на ветке, есть золотое сечение и в форме яйца, если условную линию провести через его наиболее широкую часть.

это закручивание по спирали. Еще Архимед, уделяя внимание спирали,

вывел на основе ее формы уравнение, которое и сейчас применяется в технике. Позднее Гете отмечал тяготение природы к спиральным формам, называя спираль «кривой жизни». Современными учеными было установлено, что такие проявления спиральных форм в природе как раковина улитки, расположение семян подсолнечника, узоры паутины, движение урагана, строение ДНК и даже структура галактик заключают в себе ряд Фибоначчи.

основе закона
Золотого сечения служит скрипка работы Антонио Страдивари,

созданную им в 1700 году.

Советский музыковед Э. К. Розенов отмечает поразительную точность соотношений золотого сечения в строгих и свободных формах произведений Иоганна Себастьяна Баха, что соответствует вдумчивому, сосредоточенному, технически выверенному стилю мастера. Это справедливо и в отношении выдающихся творений других композиторов, где на точку золотого сечения обычно приходится наиболее яркое или неожиданное музыкальное решение

скульптор Фидий часто использовал «золотое сечение» в

своих произведениях. Самыми знаменитыми из них были статуя Зевса Олимпийского (которая считалась одним из чудес света) и Афины Парфенос.

Зевс Олимпийский

Афина Парфенос