- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Подготовка к ЕГЭ (решение стереометрических задач) Подготовка к ЕГЭ (решение стереометрических задач)
Содержание
- 2. ПовторениеДве плоскости называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 90°Определение перпендикулярности плоскостей
- 3. Свойства перпендикулярных плоскостей1.Если прямая лежит в одной
- 4. Если одна из двух плоскостей проходит
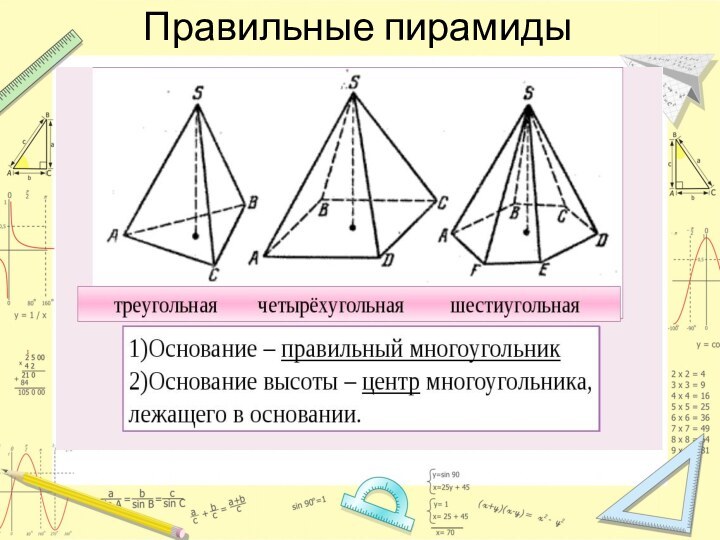
- 5. Правильные пирамиды
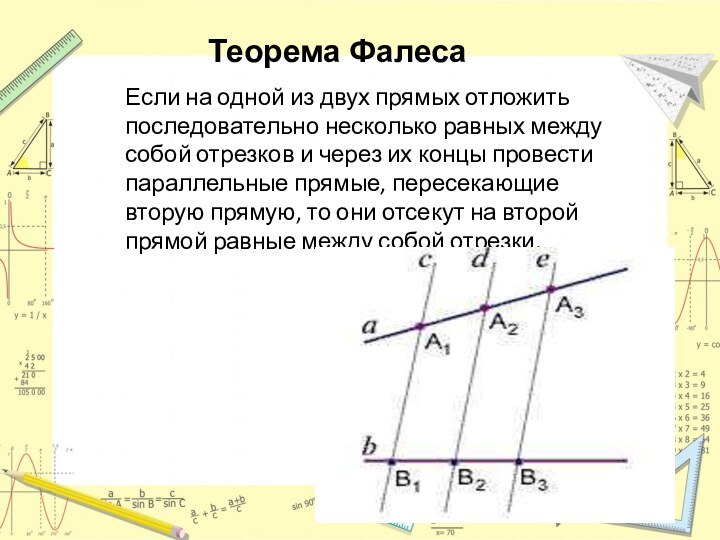
- 6. Теорема ФалесаЕсли на одной из двух
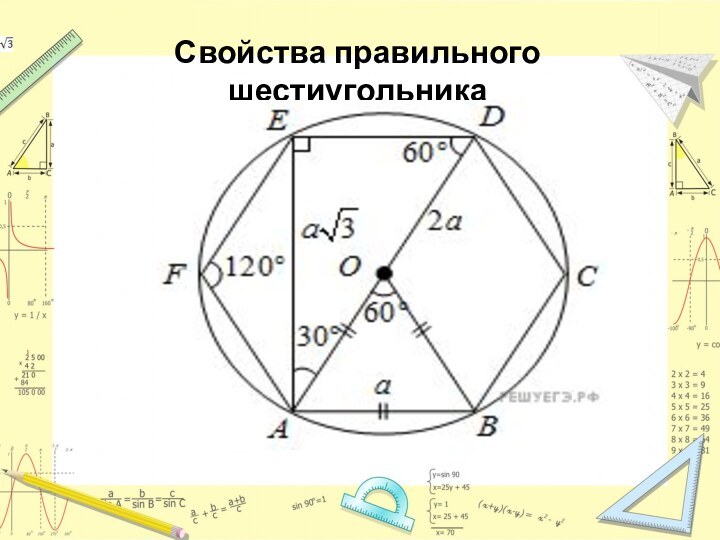
- 7. Свойства правильного шестиугольника
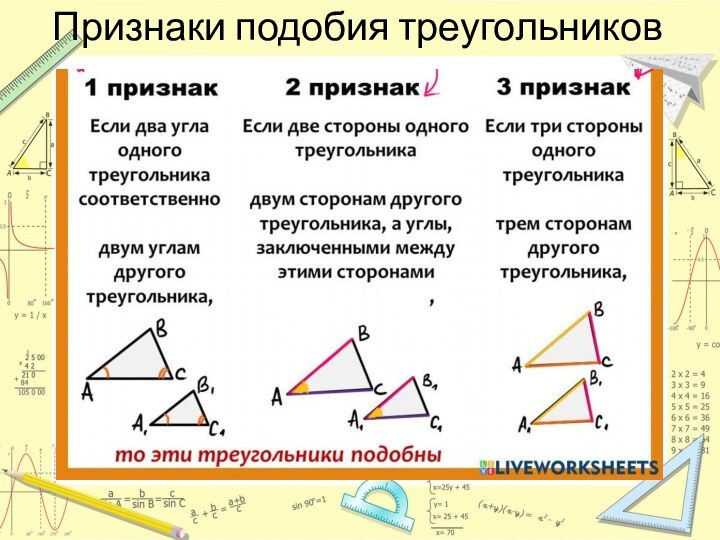
- 8. Признаки подобия треугольников
- 9. Формулы для вычисления площади треугольника
- 10. ЗадачаВ правильной шестиугольной пирамиде SABCDEF сторона основания
- 11. Дано:SABCDEF-правильная пирамида, АВ=2, SA=8, М. пл.
- 12. Решение:а)SO-высота пирамиды => SO (ABCDEF)(по
- 13. О- середина АD, FC ||АВ(по свойству правильного
- 14. б) V CDKM= 1/3*S ▲DСМ*КНS ▲DСМ найдем
- 15. ОС=АВ(по свойству правильного шестиугольника)Найдем SO по теореме
- 16. Скачать презентацию
- 17. Похожие презентации
ПовторениеДве плоскости называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 90°Определение перпендикулярности плоскостей








Слайд 2
Повторение
Две плоскости называются перпендикулярными (взаимно перпендикулярными), если угол
между ними равен 90°
Слайд 3
Свойства перпендикулярных плоскостей
1.Если прямая лежит в одной из
двух взаимно перпендикулярных плоскостей и перпендикулярна линии их пересечения, то
эта прямая перпендикулярна другой плоскости.2.Если две плоскости, перпендикулярные третьей плоскости, пересекаются, то прямая их пересечения перпендикулярна третьей плоскости.
3.Если прямая, проведённая через точку одной из двух взаимно перпендикулярных плоскостей, перпендикулярна другой плоскости, то она лежит в первой из них.
Слайд 4
Если одна из двух плоскостей проходит через
прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны
Признак перпендикулярности
двух плоскостей.
Слайд 6
Теорема Фалеса
Если на одной из двух прямых
отложить последовательно несколько равных между собой отрезков и через
их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Слайд 10
Задача
В правильной шестиугольной пирамиде SABCDEF сторона основания АВ
равна 2, а боковое ребро SA равно 8. Точка
М — середина ребра АВ. Плоскость α перпендикулярна плоскости ABC и содержит точки М и D. Прямая SC пересекает плоскость α в точке К.а) Докажите, что КМ = KD.
б) Найдите объём пирамиды CDKM.
Слайд 11
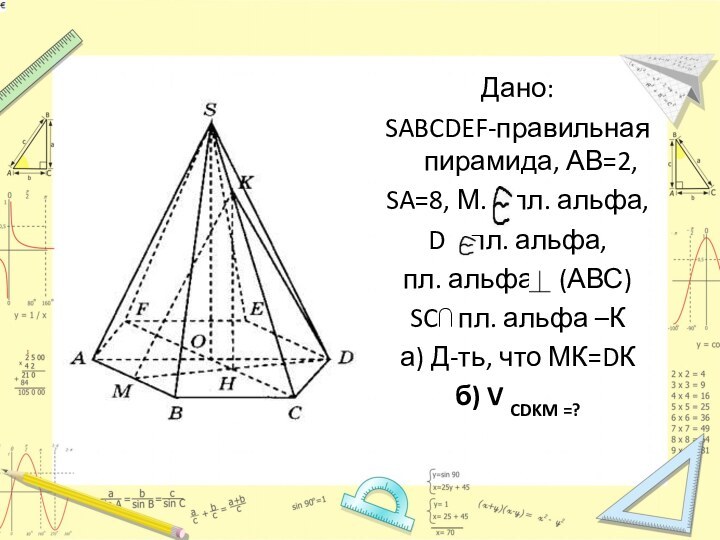
Дано:
SABCDEF-правильная пирамида, АВ=2,
SA=8, М. пл. альфа,
D пл. альфа,
пл. альфа (АВС)
SC⋂
пл. альфа –Ка) Д-ть, что МК=DК
б) V CDKM =?
Слайд 12
Решение:
а)SO-высота пирамиды =>
SO (ABCDEF)(по опр.пр.
пирамиды)
SO (SCF) =>
(SCF) (ABCDEF)(по признаку
перпендикулярности плоскостей)пл. альфа (АВС)
(SCF) ⋂ пл. альфа -КН =>
КН (ABCDEF) (по свойству перпендикулярности плоскостей) =>
КН МD =>КН-высота ▲ КМD
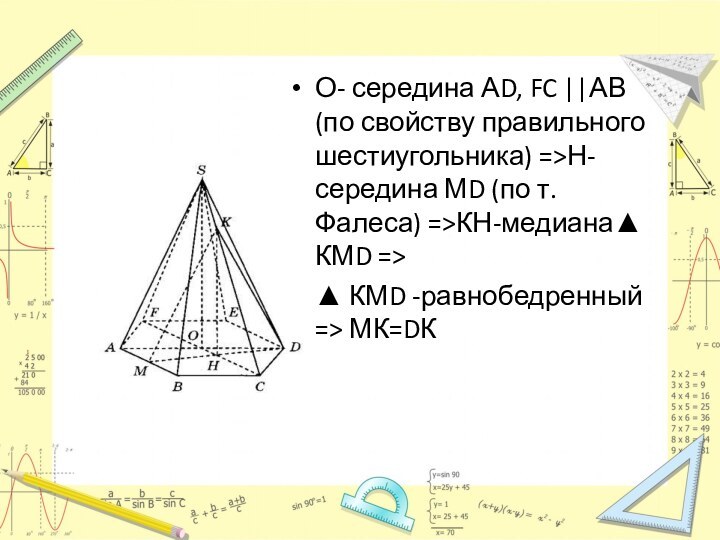
Слайд 13 О- середина АD, FC ||АВ(по свойству правильного шестиугольника)
=>Н-середина МD (по т. Фалеса) =>КН-медиана▲ КМD =>
▲
КМD -равнобедренный => МК=DК
Слайд 14
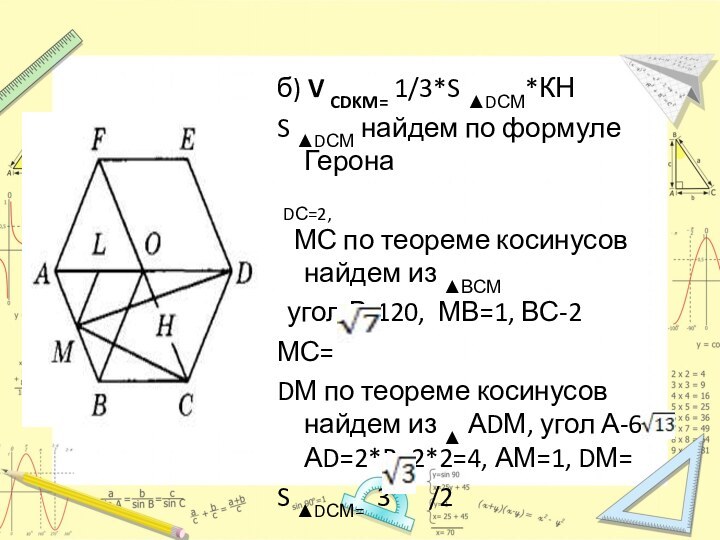
б) V CDKM= 1/3*S ▲DСМ*КН
S ▲DСМ найдем по
формуле Герона
DС=2,
МС по теореме косинусов
найдем из ▲ВСМугол В-120, МВ=1, ВС-2
МС=
DМ по теореме косинусов найдем из ▲ АDМ, угол А-60, АD=2*R=2*2=4, АМ=1, DМ=
S ▲DСМ= 3 /2
Слайд 15
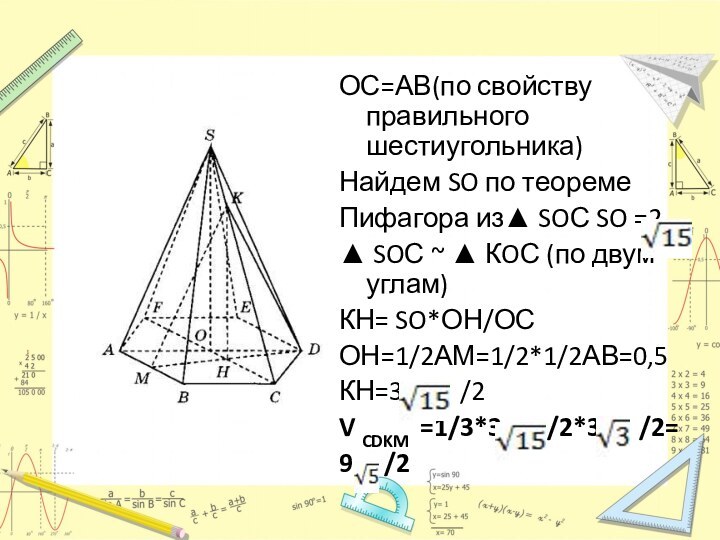
ОС=АВ(по свойству правильного шестиугольника)
Найдем SO по теореме
Пифагора
из▲ SOС SO =2
▲ SOС ~ ▲ КOС (по
двум углам)КН= SO*ОН/ОС
ОН=1/2АМ=1/2*1/2АВ=0,5
КН=3 /2
V CDKM =1/3*3 /2*3 /2=
9 /2





























