Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Конус

Содержание

2. Вот колпак на голове – Это клоун
3. КОНУС
4. И предо мной свой белый конусТы
5. Конусы в архитектуре
8. Вокруг нас…
9. Форма конуса в природе
13. \
14. Конус - происходит от греческого слова «конос» – заостренный предмет, шишка.
15. Тело, ограниченное конической поверхностью
16. Отрезки образующих, заключенные между вершиной и основанием
17. Конус – тело вращения… Конус
18. Площадь боковой поверхности конуса
20. Сечение конуса различными плоскостями.а) секущая плоскость проходит
21. Из истории исследования конических сечений Греция (
23. Конические сечения имеют интересные оптические
24. Применение конических сеченийшироко используются в оптических приборах
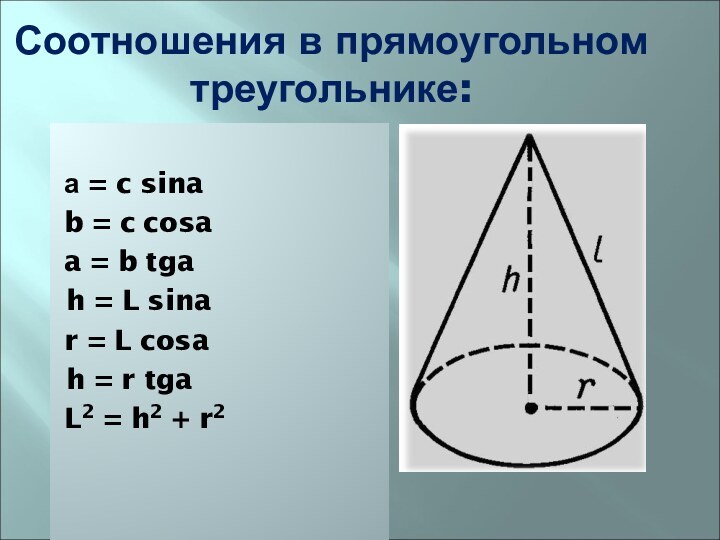
25. Соотношения в прямоугольном треугольнике: а = c
26. Дано: конус, r = 4 cмL=5 cмh=?Решение: h2=L2-r2=25-16=9h= 3смОтвет: 3см.
27. №547 ДАНО:КОНУС,H=15СМR=8СМНАЙТИ: L-?РЕШЕНИЕ:L2= H2 + R2L2 =225+64=289L=17СМОТВЕТ: 17 СМ
28. Решение задач.По учебнику: №548, №550, №553.
29. Таинственные конусы в египетской пустыне
30. Это сооружение, созданное в
31. Скачать презентацию
32. Похожие презентации

Вот колпак на голове – Это клоун на траве. Но колпак не пирамида, Это сразу, братцы, видно: Круг в основе колпака. Как же звать его тогда?

КОНУС.Презентацию подготовила преподаватель математики ГПОУ СЛТКопецкая М.Г.

И предо мной свой белый конусТы высишь, старый Арарат, В огромной шапке

Конус - происходит от греческого слова «конос» – заостренный предмет, шишка.

Тело, ограниченное конической поверхностью и кругом с границей L,

Отрезки образующих, заключенные между вершиной и основанием называются образующими конуса, а образованная

Конус – тело вращения… Конус можно получить путем вращения прямоугольного

Площадь боковой поверхности конуса За площадь боковой поверхности

Сечение конуса различными плоскостями.а) секущая плоскость проходит через ось конуса, осевое сечение

Из истории исследования конических сечений Греция ( 4 век до н. э),

Конические сечения имеют интересные оптические свойства, которые широко используются в

Применение конических сеченийшироко используются в оптических приборах (прожекторах);архитекторы используют для создания поразительных

Соотношения в прямоугольном треугольнике: а = c sinab = c cosaa =

Дано: конус, r = 4 cмL=5 cмh=?Решение: h2=L2-r2=25-16=9h= 3смОтвет: 3см.

№547 ДАНО:КОНУС,H=15СМR=8СМНАЙТИ: L-?РЕШЕНИЕ:L2= H2 + R2L2 =225+64=289L=17СМОТВЕТ: 17 СМ

Решение задач.По учебнику: №548, №550, №553.

Таинственные конусы в египетской пустыне На первый взгляд эти странные

Это сооружение, созданное в середине 1990-ых греческим художником Дэном

Домашнее заданиеКолпак к костюму клоуна имеет вид конуса, радиус основания которого равен

Слайды презентации

Слайд 2
Вот колпак на голове – Это клоун на траве. Но

Вот колпак на голове – Это клоун на траве. Но колпак

колпак не пирамида, Это сразу, братцы, видно: Круг в основе колпака. Как

же звать его тогда?

Слайд 4 И предо мной свой белый конус
Ты высишь,

И предо мной свой белый конусТы высишь, старый Арарат, В огромной

старый Арарат,
В огромной шапке Мономаха,
Как властелин окрестных гор,
Ты взнесся

от земного праха
В свободно-голубой простор.
Валерий Брюсов

Слайд 5 Конусы в архитектуре

Слайд 8 Вокруг нас…

Слайд 9 Форма конуса в природе

Слайд 14 Конус - происходит от греческого слова «конос» –

заостренный предмет, шишка.

Слайд 15
Тело, ограниченное конической поверхностью и

кругом с границей L, называется конусом.
Круг называется основанием конуса,

вершина конической поверхности – вершина конуса.

Слайд 16 Отрезки образующих, заключенные между вершиной и основанием называются

Отрезки образующих, заключенные между вершиной и основанием называются образующими конуса, а

образующими конуса, а образованная ими часть конической поверхности –

боковой поверхностью конуса.

Ось конической поверхности называется осью конуса, а ее отрезок, заключенный между вершиной и основанием, - высотой конуса.

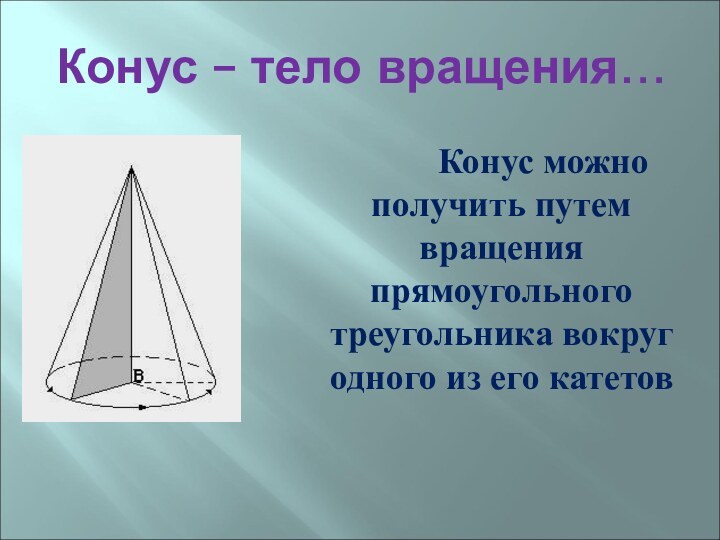
Слайд 17 Конус – тело вращения…
Конус можно

получить путем вращения прямоугольного треугольника вокруг одного из его

катетов

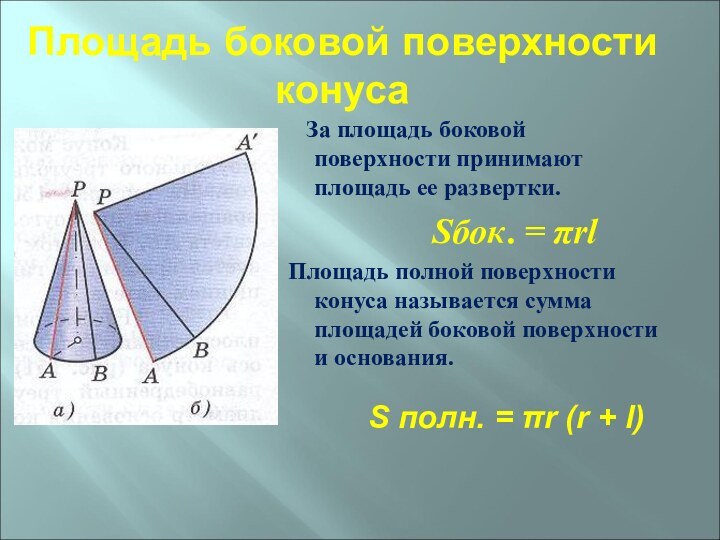
Слайд 18 Площадь боковой поверхности конуса

Площадь боковой поверхности конуса За площадь боковой поверхности принимают

За площадь боковой поверхности принимают площадь ее развертки.

Sбок. = πrl
Площадь полной поверхности конуса называется сумма площадей боковой поверхности и основания.

S полн. = πr (r + l)

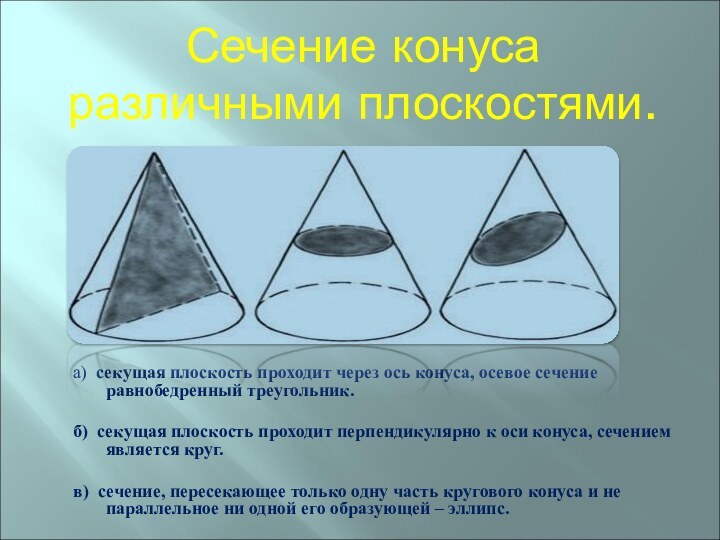
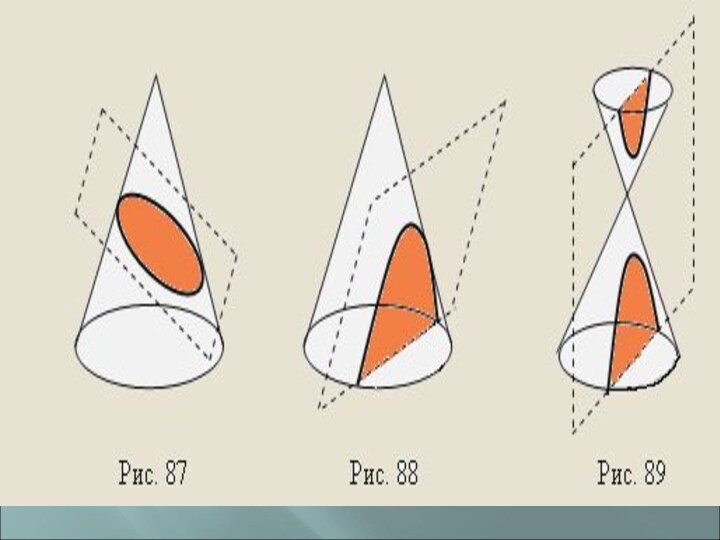
Слайд 20 Сечение конуса различными плоскостями.
а) секущая плоскость проходит через

Сечение конуса различными плоскостями.а) секущая плоскость проходит через ось конуса, осевое

ось конуса, осевое сечение равнобедренный треугольник.

б) секущая плоскость проходит

перпендикулярно к оси конуса, сечением является круг.

в) сечение, пересекающее только одну часть кругового конуса и не параллельное ни одной его образующей – эллипс.

Слайд 21 Из истории исследования конических сечений
Греция ( 4

Из истории исследования конических сечений Греция ( 4 век до н.

век до н. э), Менехм - ученик Платона, решая

задачу о удвоении куба получил 3 вида кривых:
эллипс,
параболу,
гиперболу.
Конические сечения подробно исследовал Аполлоний Пергский (3в.-2в. до н. э.)

Слайд 23 Конические сечения имеют интересные оптические свойства,

которые широко используются в технике. Это основано на свойствах

конических сечений- эллипса, гиперболы и параболы - и поверхностей, образованных вращением этих кривых

Слайд 24 Применение конических сечений
широко используются в оптических приборах (прожекторах);
архитекторы

Применение конических сеченийшироко используются в оптических приборах (прожекторах);архитекторы используют для создания

используют для создания поразительных звуковых эффектов: «говорящих» бюстов, «

мистического» шепота
« потусторонних» звуков;
по эллиптическим, параболическим или гиперболическим орбитам движутся тела в поле тяготения.

Слайд 25 Соотношения в прямоугольном треугольнике:

а = c sina
b =

c cosa
a = b tga
h = L sina
r

= L cosa
h = r tga
L2 = h2 + r2

Слайд 26 Дано: конус,
r = 4 cм
L=5 cм
h=?
Решение:
h2=L2-r2=25-16=9
h=

3см
Ответ: 3см.

Слайд 27 №547
ДАНО:
КОНУС,
H=15СМ
R=8СМ
НАЙТИ: L-?
РЕШЕНИЕ:
L2= H2 + R2
L2 =225+64=289
L=17СМ
ОТВЕТ: 17

СМ

Слайд 28 Решение задач.
По учебнику: №548, №550, №553.

Слайд 29 Таинственные конусы в египетской пустыне
На

первый взгляд эти странные конусы и воронки из египетской

пустыни кажутся всего лишь необычными ветровыми образованиями, но стоит подняться на высоту птичьего полета, и вы увидите узор, который они формируют.

постройки инопланетян, или утерянной цивилизации?

Слайд 30 Это сооружение, созданное в середине

1990-ых греческим художником Дэном Страту (Danae Stratou) и группой

DAST, называется «Дыхание пустыни». Оно занимает площадь 100 000 квадратных метров и расположено в пустыни в Египте неподалеку от Красного моря. Создание этого произведения искусства заняло несколько лет. В центре находился довольно глубокий бассейн с водой, а весь проект был выполнен так, чтобы со временем постепенно разрушаться от эрозии. Что, как видно, и произошло.