Презентация на тему Поиск возможности использования графического метода решения уравнений III и IV степени

Содержание

2. Уравнения первой степениСреднеазиатский математик ал-Хорезми в IX
3. Уравнения второй степениНеобходимость решать уравнения не только
4. Кубические уравненияАлгебраическое решение кубического уравнения, т.е. открытие
5. Формула Кардано — формула для нахождения корней канонической
6. Уравнение четвёртой степениГрафик многочлена 4-ой степени с
7. Скачать презентацию
8. Похожие презентации

Уравнения первой степениСреднеазиатский математик ал-Хорезми в IX веке установил, что решение уравнений первой степени сводится к двум операциям: к переносу отдельных членов его из одной части равенства в другую и приведение подобных членов.

Главная
Образование
Презентация Поиск возможности использования графического метода решения уравнений III и IV степени

Поиск возможности использования графического метода решения уравнений III и IV степени

Уравнения первой степениСреднеазиатский математик ал-Хорезми в IX веке установил, что решение уравнений

Уравнения второй степениНеобходимость решать уравнения не только первой, но и второй степени

Кубические уравненияАлгебраическое решение кубического уравнения, т.е. открытие формулы, которая позволяет выразить корни

Формула Кардано — формула для нахождения корней канонической формы кубического уравнения

Уравнение четвёртой степениГрафик многочлена 4-ой степени с четырьмя корнями и тремя критическими

Слайды презентации

Слайд 2 Уравнения первой степени
Среднеазиатский математик ал-Хорезми в IX веке

Уравнения первой степениСреднеазиатский математик ал-Хорезми в IX веке установил, что решение

установил, что решение уравнений первой степени сводится к двум

операциям: к переносу отдельных членов его из одной части равенства в другую и приведение подобных членов.

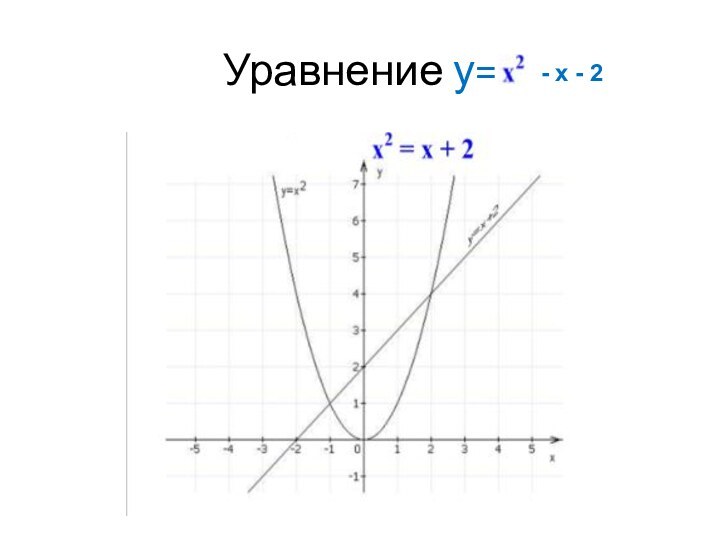
Слайд 3 Уравнения второй степени
Необходимость решать уравнения не только первой,

Уравнения второй степениНеобходимость решать уравнения не только первой, но и второй

но и второй степени еще в древности была вызвана

потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне.

Слайд 4 Кубические уравнения
Алгебраическое решение
кубического уравнения,
т.е. открытие формулы,

Кубические уравненияАлгебраическое решение кубического уравнения, т.е. открытие формулы, которая позволяет выразить

которая позволяет
выразить корни уравнения
через его коэффициенты,
было

найдено в XVI веке
итальянскими математиками
Ферро, Тарталье и Кардано.

ФЕРРО

КАРДАНО

Слайд 5 Формула Кардано — формула для нахождения корней канонической формы

кубического уравнения

над полем комплексных чисел.

Любое кубическое уравнение общего вида
может быть приведено к указанной выше канонической форме с коэффициентами p и q:

при помощи подходящей замены переменной вида .

Подставляя три последние формулы в соответствующее кубическое уравнение, находим эту замену: