- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Правильные многогранники
Содержание
- 2. Что такое правильный многогранник? Правильный
- 3. Определение Многогранник называется правильным, если:он выпуклый;все его грани являются равными правильными многоугольниками;в каждой его вершине сходится одинаковое число рёбер.
- 4. Виды правильных многогранниковВ трёхмерном евклидовом пространстве существует всего пять
- 5. Простейшим среди многогранников является тетраэдр (четырёхгранник –
- 6. Куб, или гексаэдр (шестигранник – от греческого
- 7. Октаэдр (восьмигранник – от греческого «окта», т.е.
- 8. Икосаэдр (двадцатигранник – от греческого «икос», т.е.
- 9. И загадочный додекаэдр (двенадцатигранник – от греческого
- 10. Философ Платон и четыре стихии природы Подробно
- 11. Платон являлся основателем школы, названной «Академией» по
- 12. Итак, правильных многогранников Платон знал пять, а
- 13. Из внешнего вида правильных многогранников следует, что
- 14. Итак, тетраэдр символизировал огонь, т.к. его вершина
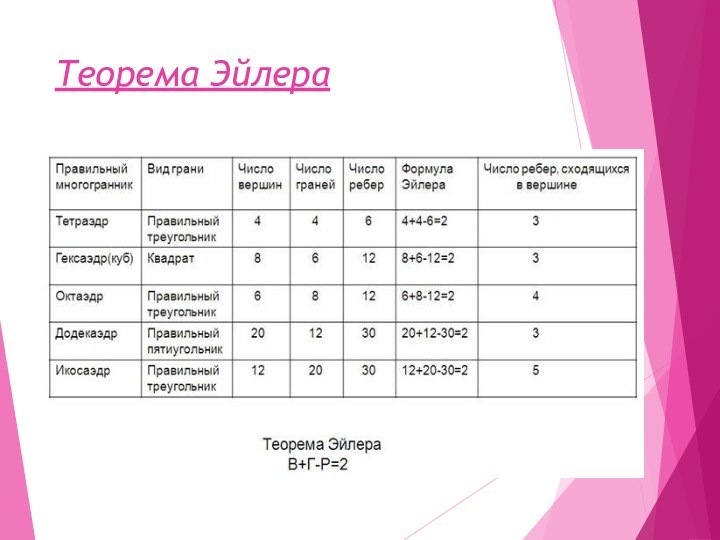
- 15. Комбинаторные свойстваЭйлером была выведена формула, связывающая число вершин
- 16. Теорема Эйлера
- 17. Многогранники в архитектуреИспользовать многогранники в архитектуре люди стали очень давно,
- 18. Национальная библиотека — одна из них.
- 19. Многогранники в архитектуреСовременный стеклянный вход в Лувр, который
- 20. Многогранники в архитектуреУсеченная пирамида пользуется популярностью у современных
- 21. Многогранники в архитектуреА это парк развлечений Футуроскоп под Парижем (Франция)
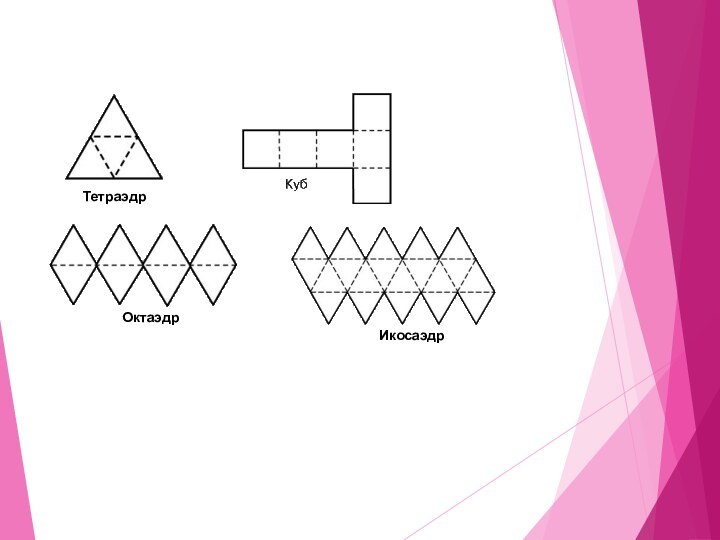
- 22. Развёртки правильных многогранников Одним из способов изготовления
- 23. Скачать презентацию
- 24. Похожие презентации
Что такое правильный многогранник? Правильный многогранник или плато́ново тело — это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий пространственной симметрией.





















Слайд 3
Определение
Многогранник называется правильным, если:
он выпуклый;
все его грани являются
равными правильными многоугольниками;
в каждой его вершине сходится одинаковое число рёбер.
Слайд 4
Виды правильных многогранников
В трёхмерном евклидовом пространстве существует всего пять правильных
многогранников:
Название каждого многогранника происходит от греческого названия количества его
граней и слова «грань».Слайд 5 Простейшим среди многогранников является тетраэдр (четырёхгранник – от
греческого «тетра», т.е. четыре).
Его четыре грани – равносторонние
треугольники. Четыре – это наименьшее число граней, отделяющих часть трёхмерного пространства. Тем не менее, тетраэдр обладает многими свойствами, характерными для однородных многогранников. Все его грани суть правильные многоугольники, причём каждая отделяется ребром в точности от одной грани. Все многогранные углы тетраэдра также равны между собой.Слайд 6 Куб, или гексаэдр (шестигранник – от греческого «гекса»,
т.е. шесть) – самый общеизвестный и широко используемый многогранник.
Все шесть его граней – квадраты, сходящиеся по два вдоль каждого ребра и по три в каждой вершине.
Слайд 7 Октаэдр (восьмигранник – от греческого «окта», т.е. восемь),
составленный из восьми правильных треугольников, его противоположные грани лежат
в параллельных плоскостях.Иоганн Кеплер (1571-1630) в своём этюде «О снежинке» высказал такое замечание: «Среди правильных тел самое первое, начало и родитель остальных – куб, а его, если позволительно так сказать, супруга – октаэдр, ибо у октаэдра столько углов, сколько у куба граней».
Слайд 8 Икосаэдр (двадцатигранник – от греческого «икос», т.е. двадцать),
составленный из двадцати правильных треугольников.
Икосаэдр – одно из пяти
тел, по простоте следующее за тетраэдром и октаэдром. Их объединяет то обстоятельство, что гранями каждого являются равносторонние треугольники.
Слайд 9
И загадочный
додекаэдр (двенадцатигранник – от греческого «додека»,
т.е. двенадцать), составленный из двенадцати правильных пятиугольников. В известном
смысле додекаэдр представляет наибольшую привлекательность среди тел, соперничая с икосаэдром, который почти ему не уступает (а быть может, в чём-то и превосходит).
Слайд 10
Философ Платон и четыре стихии природы
Подробно описал свойства
правильных многогранников древнегреческий учёный, философ-идеалист Платон
(428 –348 до
н.э.), в учении которого они играли важную роль. Поэтому эти многогранники носят название «платоновых тел».Слайд 11 Платон являлся основателем школы, названной «Академией» по имени
местности вблизи Афин, где он постоянно встречался со своими
учениками. Сам Платон не был математиком, но он придавал ей исключительно важное значение. При входе в основанную им Академию была надпись следующего содержания: «Пусть сюда не входит тот, кто не знает геометрии …». Одному из желающих поступить в его школу для изучения философии, но не имеющему знаний по геометрии, Платон сказал: «Уйди прочь! У тебя нет орудия для изучения философии …».Платон связал с этими телами формы атомов основных стихий природы. Какими соображениями при этом он руководствовался?
Слайд 12 Итак, правильных многогранников Платон знал пять, а число
стихий (огонь, воздух, вода и земля) было ровно четыре.
Следовательно, из пяти многогранников надо выбрать четыре, которые можно было бы сопоставить со стихиями. Платон считал, что некоторые элементы правильных многогранников могут перейти друг в друга. Преобразование одних многогранников в другие могли быть осуществлены путем перестройки их внутренней структуры. Но для этого в данных телах нужно было найти такие структурные элементы, которые были бы для них общими.Слайд 13 Из внешнего вида правильных многогранников следует, что грани
трех многогранников – тетраэдра, октаэдра, икосаэдра – имеют форму
равностороннего треугольника. Два оставшихся многогранника – куб и додекаэдр – построены: первый – из квадратов, а второй – из правильных пятиугольников, поэтому они не могут преобразовываться ни друг в друга, ни в рассмотренные три тела.
Слайд 14
Итак,
тетраэдр символизировал огонь, т.к. его вершина устремлена
вверх.
Куб или гексаэдр символизировал – землю, как самый
"устойчивый". Октаэдр символизирует воздух, как самый "воздушный".
Икосаэдр символизирует – воду, т.к. он самый "обтекаемый".
И всей вселенной была приписана форма додекаэдра, т. е. мы живём внутри небесного свода.
Слайд 15
Комбинаторные свойства
Эйлером была выведена формула, связывающая число вершин (В),
граней (Г) и рёбер (Р) любого выпуклого многогранника простым соотношением: В
+ Г = Р + 2.Отношение количества вершин правильного многогранника к количеству рёбер одной его грани равно отношению количества граней этого же многогранника к количеству рёбер, выходящих из одной его вершины. У тетраэдра это отношение равно 4:3, у гексаэдра и октаэдра — 2:1, а у додекаэдра и икосаэдра — 4:1.
Правильный многогранник может быть комбинаторно описан символом Шлефли {p, q}, где: p — число рёбер в каждой грани; q — число рёбер, сходящихся в каждой вершине.





























