- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Степенная функция (обобщающее занятие)
Содержание
- 2. «Пусть кто-нибудь попробует вычеркнуть из математики степени,
- 3. Содержание
- 4. «Математика, вероятно, никогда не достигла бы такой
- 5. Пятое действие арифметикиПотребность в действиях возведения в
- 6. Шестое действие арифметикиЕще 4000 лет назад вавилонские
- 7. Биографические сведения о Рене ДекартеЧесть придания алгебре
- 8. Биографические сведения о Рене ДекартеШвецией в это
- 9. «Мало иметь хороший ум, главное – хорошо
- 10. Применение степенной функцииСТЕПЕНЬ С натуральным четным ПОКАЗАТЕЛЕМ
- 11. Применение степенной функцииСТЕПЕНЬ С натуральным нечетным показателем – кубическая параболаСтрелочный перевод
- 12. Применение степенной функцииСТЕПЕНЬ С ОТРИЦАТЕЛЬНЫМ ДРОБНЫМ ПОКАЗАТЕЛЕМ - гиперболаВ экономике – функции спроса; кривые безразличия
- 13. Применение степенной функцииСТЕПЕНЬ С положительным ДРОБНЫМ ПОКАЗАТЕЛЕМ
- 14. Применение степенной функцииМногие функциональные зависимости выражаются через
- 15. Применение степенной функции в экономикеВ экономике используются
- 16. Применение степенной функции в физикеМногие физические зависимости
- 17. Задача:На учебном полигоне произведён выстрел из зенитного
- 18. «Русский народ создал огромную изустную литературу...
- 19. Степенная функция в пословицах и поговорках«Чем дальше
- 20. Степенная функция в пословицах и поговорках« Поменьше говори, побольше услышишь»«Как аукнется, так и откликнется»
- 21. Степенная функция в пословицах и поговорках«Недосол на столе – пересол на спине»«Душа в пятки ушла»
- 22. «Счет и вычисления - основа порядка в голове» Иоганн Генрих Песталоцци, швейцарский педагог (1746-1827) Викторина
- 23. 1. Функция у = 1/х является степенной.
- 24. y = 3х + 5y = 3/(
- 25. 3. Найдите область определения функции у = (3х + 1)-2 х-1/3
- 26. 4. Найдите множество значений функции у = х - 4(0; +)
- 27. 5. Функция у = х1/3 является возрастающей на всей области определения.
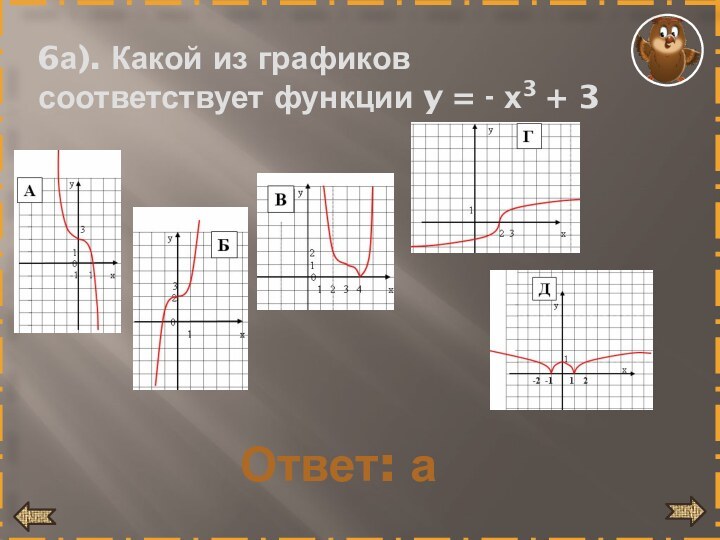
- 28. 6а). Какой из графиков соответствует функции y = - х3 + 3Ответ: а
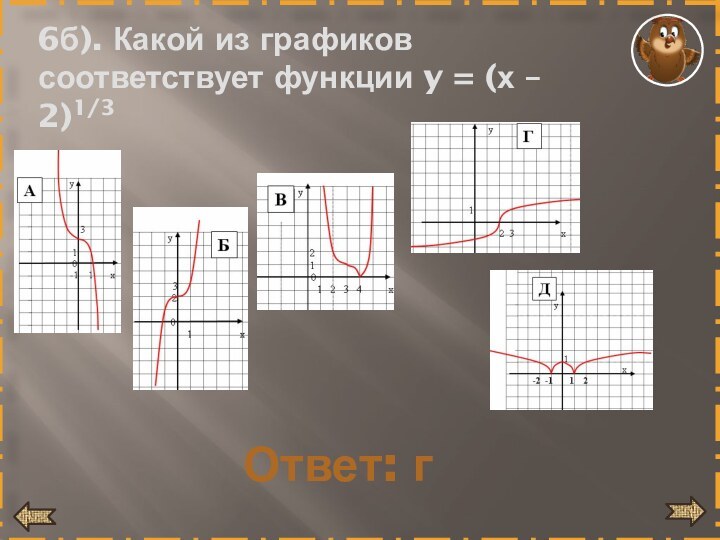
- 29. 6б). Какой из графиков соответствует функции y = (х – 2)1/3 Ответ: г
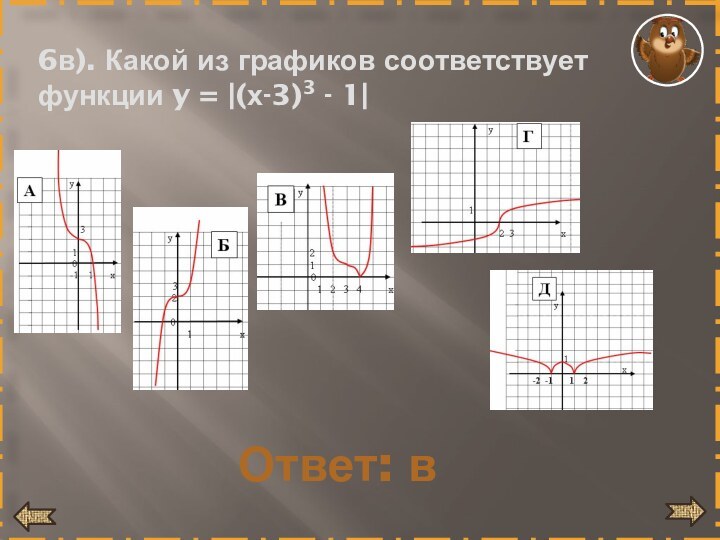
- 30. 6в). Какой из графиков соответствует функции y = (х-3)3 - 1Ответ: в
- 31. 7. В каком случае уравнения являются равносильными?(х
- 32. 8. Найдите область определения уравнения -3;0
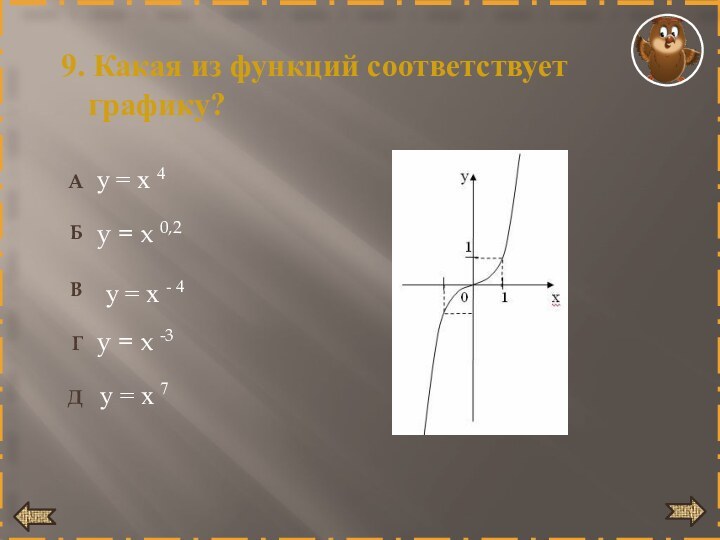
- 33. 9. Какая из функций соответствует графику?у =
- 34. возведение в квадрат с последующей проверкойграфическийзамена переменнойиспользование
- 35. 11. Какая из функций является нечетной:у =
- 36. Домашнее заданиеАлимов Ш.А. и др. Алгебра и
- 37. Скачать презентацию
- 38. Похожие презентации
«Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь» М.В. Ломоносов, русский ученый (1711-1765)



























Слайд 4 «Математика, вероятно, никогда не достигла бы такой высокой
степени совершенства, если бы древние не приложили столько усилий
для изучения вопросов, которыми сегодня многие пренебрегают из-за их мнимой бесплодности» Леонард Эйлер, швейцарский математик, механик (1707-1783)
Слайд 5
Пятое действие арифметики
Потребность в действиях возведения в степень
и извлечения корня была вызвана практической необходимостью.
Представление о возведении
в степень как о самостоятельной операции сложилось не сразу, хотя задачи на вычисление степеней встречаются еще в математических текстах Древнего Египта и Междуречья. Глиняные плитки содержат записи таблиц квадратов, кубов и их обратных значений.Первоначально под степенью понимали произведение нескольких одинаковых сомножителей.
В XIV в. французский епископ города Лизье в Нормандии Никола Орем впервые стал заменять корни из чисел дробными показателями степени.
Английский математик Джон Валлис в 1665 г. впервые подробно рассмотрел вопрос о целесообразности употребления отрицательных показателей.
Современное обозначение натуральной степени впервые ввел Декарт, а отрицательных степеней - И. Ньютон в 1676 году.
Слайд 6
Шестое действие арифметики
Еще 4000 лет назад вавилонские ученые
умели находить приблизительные значения квадратного корня из любого целого
числа.Среди знаменитых задач, которыми занимались древнегреческие ученые еще в V – IV вв. до н.э., была задача «об удвоении куба»: «Найти ребро куба, объем которого в 2 раза больше объема данного куба». Схему для приближенного извлечения кубических корней дал греческий математик Герон Александрийский в I в. н.э.
Приемы извлечения кубического и квадратного корня с помощью счетной доски и счетных палочек содержатся в китайском трактате XIII в. «Математика в девяти книгах».
Слово «корень» пришло от арабов, которые представляли себе квадрат числа, вырастающим из корня, как растение.
Современный знак корня ввел Рене Декарт в 1637 году, однако во всеобщее употребление он вошел лишь в начале XVIII в. Тогда же было установлено, что квадратный корень из положительного числа имеет два значения – положительное и отрицательное, а из отрицательного числа квадратный корень извлекать нельзя.
Слайд 7
Биографические сведения о Рене Декарте
Честь придания алгебре современного
вида принадлежит Р. Декарту.
Рене Декарт родился в маленьком
городке Лаэ провинции Турень, в не очень знатной, но зажиточной дворянской семье. Его мать умерла, когда ему был 1 год. Отец Декарта был судьёй. В детстве Рене отличался хрупким здоровьем и невероятной любознательностью.В восемь лет Рене отдали на полное попечение в одну из лучших иезуитских коллегий. Впоследствии Декарт с благодарностью вспоминал о заботах ее воспитателей.
Парадоксально, но именно иезуиты, учителя Декарта, станут потом его заклятыми врагами. Декарта стали преследовать за его философское учение, и он был вынужден искать убежища в Голландии, где прожил около 20 лет. Однако, это его не спасло. Произведения Декарта были присуждены сожжению.
Он ведёт обширную переписку с лучшими учёными Европы, изучает самые различные науки – от медицины до метеорологии. Декарт сформулировал свой метод познания: дедуктивные (математические) рассуждения над результатами воспроизводимых опытов.
Слайд 8
Биографические сведения о Рене Декарте
Швецией в это время
правила 20-летняя королева Кристина Августа. Энергичная королева обладала незаурядными
способностями. Она пригласила к себе Декарта в 1649 году для занятий философией.Несмотря на зимние холода, уроки начинались в пять утра. Это было тяжело для Декарта. Однажды, направляясь во дворец, он простудился. началось воспаление легких, и 11 февраля 1650 года Декарт умер.
В 1980 г. в архиве Лейденского университета нашлось письмо личного врача королевы Кристины, которое показывает, что ученый умер не от воспаления легких, а был отравлен. Предполагают, что это было сделано из опасения влияния католика Декарта на протестантку Кристину. Тем не менее через четыре года после смерти ученого королева отреклась от престола, перешла в католичество и уехала в Италию.
Так спустя 330 лет после смерти, возможно, была раскрыта тайна гибели великого Декарта.
Слайд 9 «Мало иметь хороший ум, главное – хорошо его
применять»
Рене Декарт, французский философ, математик (1596 -1650)
Слайд 10
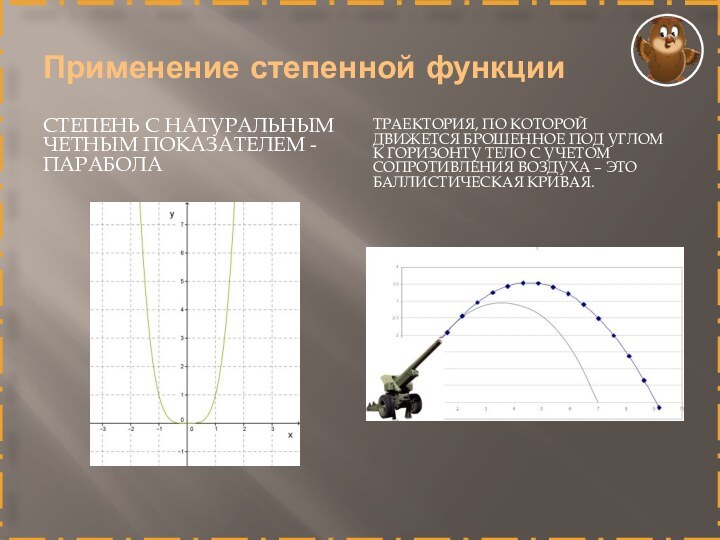
Применение степенной функции
СТЕПЕНЬ С натуральным четным ПОКАЗАТЕЛЕМ -
парабола
Траектория, по которой движется брошенное под углом к горизонту
тело с учетом сопротивления воздуха – это баллистическая кривая.
Слайд 11
Применение степенной функции
СТЕПЕНЬ С натуральным нечетным показателем –
кубическая парабола
Стрелочный перевод
Слайд 12
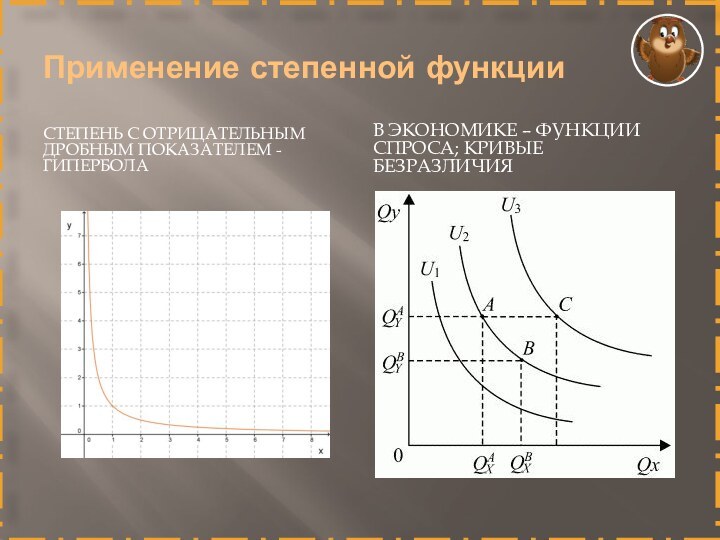
Применение степенной функции
СТЕПЕНЬ С ОТРИЦАТЕЛЬНЫМ ДРОБНЫМ ПОКАЗАТЕЛЕМ -
гипербола
В экономике – функции спроса; кривые безразличия
Слайд 13
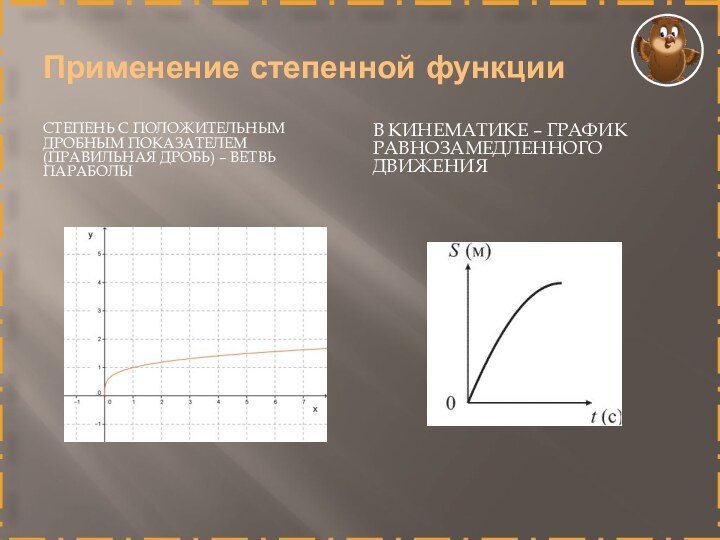
Применение степенной функции
СТЕПЕНЬ С положительным ДРОБНЫМ ПОКАЗАТЕЛЕМ (правильная
дробь) – ветвь параболы
В кинематике – график равнозамедленного движения
Слайд 14
Применение степенной функции
Многие функциональные зависимости выражаются через степенную
функцию. Например,
В геометрии зависимость объема куба V
от его ребра a: V = a3;
В географии дальность d расстояния горизонта от наблюдателя - это функция высоты, на которую поднят наблюдатель над уровнем моря:
d = 3,8h1/2;
В строительстве сопротивление балки изгибу зависит от момента инерции сечения относительно нейтрального слоя. Момент инерции для круглой балки радиуса R равен
R2/4,
а для квадратного сечения со стороной а:
а4/12,
где - плотность материала на единицу площади.
Слайд 15
Применение степенной функции в экономике
В экономике используются функции
полезности, показывающие отношение потребителя к товару.
Функции полезности, описывающие поведение
человека в зависимости от характера, темперамента, отношения к риску:Ровное отношение – полезность оценивается пропорционально количеству купленного;
Осторожное отношение – полезность больших приобретений преуменьшается, а «вредность» больших потерь преувеличивается;
Смелое отношение – полезность больших приобретений преувеличивается, а «вредность» больших потерь преуменьшается.
Слайд 16
Применение степенной функции в физике
Многие физические зависимости выражаются
через степенную функцию. Например,
сила притяжения F двух
тел массами m1 и m 2 зависит от расстояния r между ними: F = γ m1m2r – 2 ;
зависимость между расстоянием h и временем t при свободном падении с начальной скоростью v0 такова:
где g – ускорение свободного падения;
зависимость периода колебаний математического маятника T от его длины x:
T = 2(x/g)1/2;
зависимость давления газа P при расширении или сжатии без теплообмена с окружающей средой от его объема V:
V· Pk = C
(для воздуха k = -1,4).
Заметим, что в двух последних случаях показатель степени не является целым числом.
Слайд 17
Задача:
На учебном полигоне произведён выстрел из зенитного орудия
в вертикальном направлении. Требуется определить наибольшую высоту подъёма снаряда,
время подъёма и время падения, если начальная скорость снаряда v0 = 400 м/с. Сопротивлением воздуха пренебречь.Слайд 18 «Русский народ создал огромную изустную литературу... Напрасно
думать, что эта литература была лишь плодом народного досуга.
Она была достоинством и умом народа» А.Н. Толстой, русский писатель (1882-1945)
Слайд 19
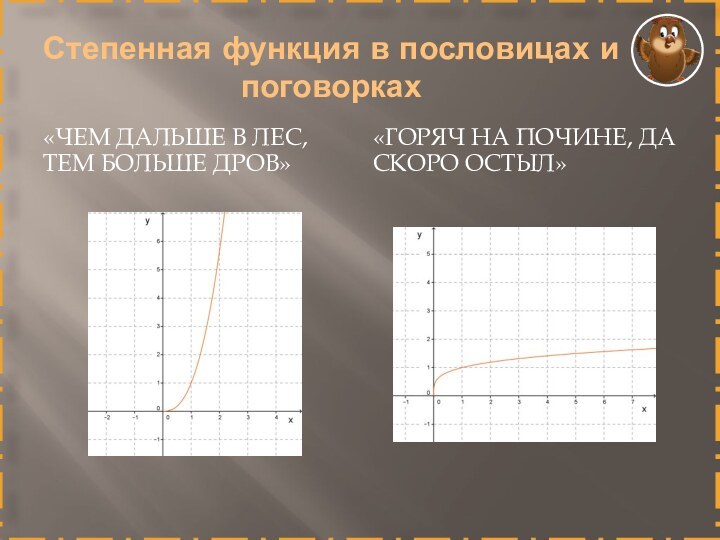
Степенная функция в пословицах и поговорках
«Чем дальше в
лес, тем больше дров»
«Горяч на почине, да скоро остыл»
Слайд 20
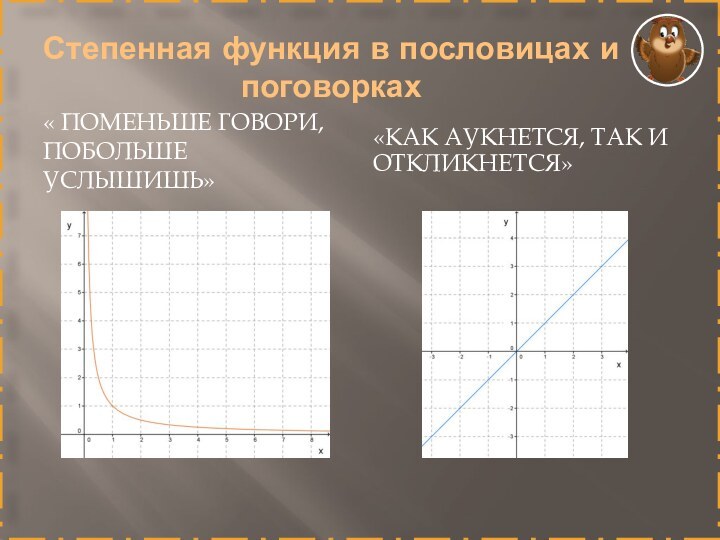
Степенная функция в пословицах и поговорках
« Поменьше говори,
побольше услышишь»
«Как аукнется, так и откликнется»
Слайд 21
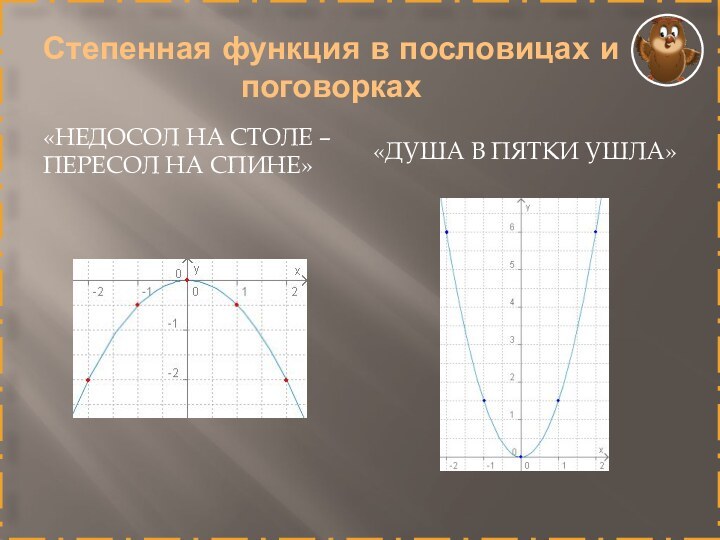
Степенная функция в пословицах и поговорках
«Недосол на столе
– пересол на спине»
«Душа в пятки ушла»
Слайд 22 «Счет и вычисления - основа порядка в
голове»
Иоганн Генрих Песталоцци, швейцарский педагог (1746-1827)
Викторина
Слайд 24
y = 3х + 5
y = 3/( х
– 5)
y = 5х – 3
y = 5/(3
– х)y = (х – 5)1/3
у = 1/5· (х + 3)
у = х3 + 5
у = 1/3· (х - 5)
у = 3 – 5/х
у = 3/х + 5
2. Установите пары взаимно обратных функций
Слайд 31
7. В каком случае уравнения являются равносильными?
(х –
5)2 = 3(х – 5) и х
– 5 = 3х – 1 = 0 и 2х – 1 = 0
(2х – 3)2 = 25 и 2х – 3 = 5
(х2 – 3х + 2)/(х – 1) = 0 и х2 – 3х + 2 = 0
(х + 18)1/3 = (2 – х)1/3 и х + 18 = 2 – х
Слайд 34
возведение в квадрат с последующей проверкой
графический
замена переменной
использование свойства
монотонности функции
оценка ОДЗ
10. Подберите для каждого уравнения предпочтительный метод
решения
Слайд 36
Домашнее задание
Алимов Ш.А. и др. Алгебра и начала
анализа. 10-11 кл. - Упр. к главе 3, «Проверь
себя»Составить глоссарий по теме: «Понятие, свойства и графики функций»





























