Презентация на тему Задание №16 ОГЭ по математике 2021

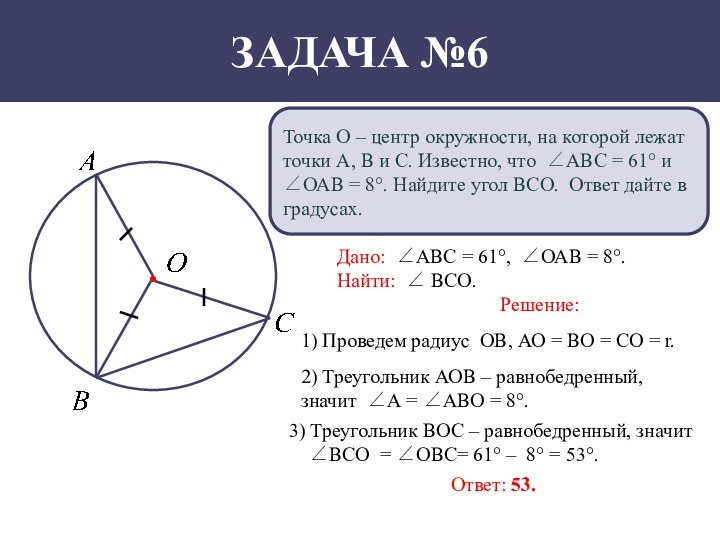
равен 38°, ∠САD равен 33°. Найдите угол АВD. Ответ

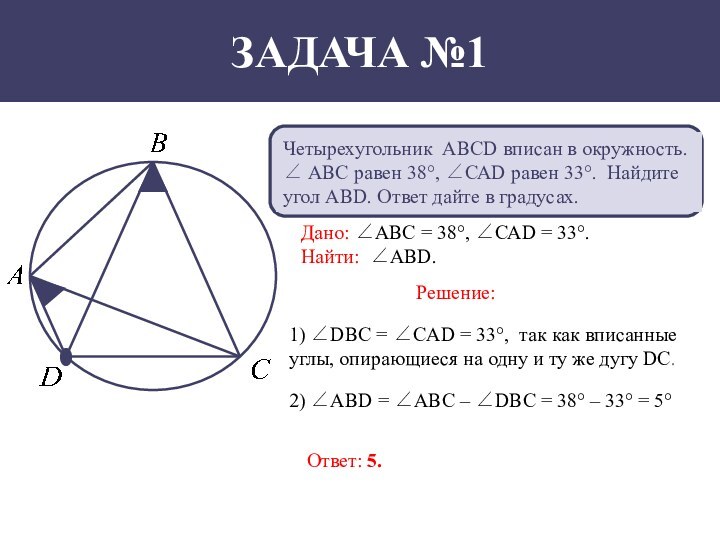
дайте в градусах.

Дано: ∠АВС = 38°, ∠САD = 33°.
Найти: ∠АВD.

Решение:

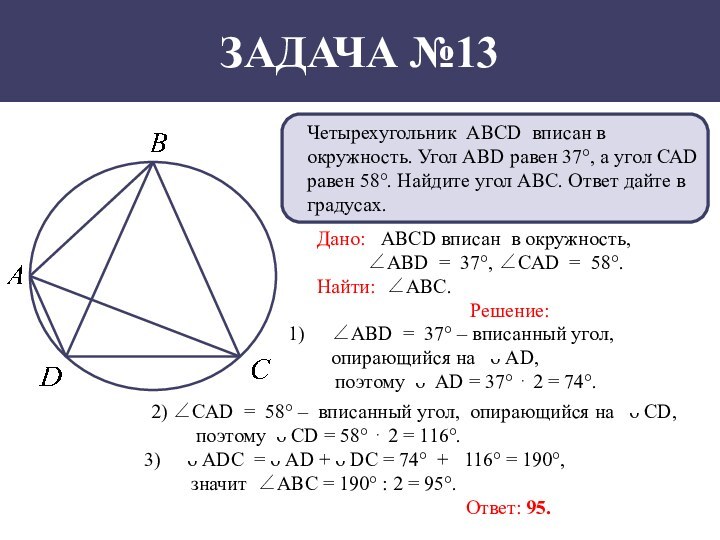
1) ∠DBC = ∠CAD = 33°, так как вписанные углы, опирающиеся на одну и ту же дугу DC.

2) ∠АВD = ∠AВC – ∠DBC = 38° – 33° = 5°

Ответ: 5.

круга, центральный угол которого равен 120°.
Дано: Sкруга = 69,

угол кругового сектора равен 120°.
Найти: Sсектора.

Решение:

Ответ: 23.

Задача №2

33°. Найдите угол С этого четырехугольника. Ответ дайте в

градусах.

Дано: АВСD вписан в окружность, ∠А = 33°.
Найти: ∠С.

Решение:

∠C = 180° – ∠A = 180° – 33° = 147°, так как сумма противоположных углов вписанного четырехугольника равна 180°.

Ответ: 147.

Задача №3

центром О. Угол АСВ равен 53°. Найдите угол АОD.

Ответ дайте в градусах.

Дано: АС и BD – диаметры окружности,
∠АСВ = 53°.
Найти: ∠ АОD.

Решение:

1) АCВ = 53° – вписанный угол, опирающийся
на ᴗ АВ, поэтому ᴗ АВ = 53°  2 = 106°, так как вписанный угол измеряется половиной дуги, на которую он опирается.

Ответ: 74.

2) BD – диаметр, значит ᴗ ВАD = 180°.

3) ∠ АОD – центральный угол, опирающийся на ᴗ АD, следовательно ∠ АОD = ᴗ АD = 180° – 106° = 74°.

Задача №4

стороне АВ. Радиус окружности равен 20,5. Найдите ВС, если

АС = 9.

Дано: АВ – d; r = 20,5; АС = 9.
Найти: ВС.

Решение:

1) ∠C = 90°, так как угол, опирающийся на диаметр, значит треугольник АВС прямоугольный.

Ответ: 40.

2) r = 20,5, следовательно АВ = 20,5  2 = 41

3) По теореме Пифагора: АВ2 = АС2 + ВС2
412 = 92 + ВС2 ВС2 = 1681 – 81
ВС2 = 1600 ВС = 40

Задача №5

точки А, В и С. Известно, что ∠АВС =

61° и ∠ОАВ = 8°. Найдите угол ВСО. Ответ дайте в градусах.

Дано: ∠АВС = 61°, ∠ОАВ = 8°.
Найти: ∠ ВСО.

Решение:

1) Проведем радиус ОВ, АО = ВО = СО = r.

Ответ: 53.

2) Треугольник АОВ – равнобедренный, значит ∠А = ∠АВО = 8°.

3) Треугольник ВОС – равнобедренный, значит
∠ВСО = ∠ОВС= 61° – 8° = 53°.

Задача №6

и В так, что : ∠АОВ = 45°. Длина

меньшей дуги равна 91. Найдите длину большей дуги.

Дано: ∠АОВ = 45°, длина меньшей дуги
равна 91.
Найти: длину большей дуги.

Решение:

Ответ: 637.

Задача №7

33°. Найдите угол С этого четырехугольника. Ответ дайте в

градусах.

Дано: АВСD вписан в окружность,
∠А = 77°.
Найти: ∠С.

Решение:

∠C = 180° – ∠A = 180° – 77° = 103°, так как сумма противоположных углов вписанного четырехугольника равна 180°.

Ответ: 103.

Задача №8

ВС = 12, СD = 13. Найдите АD.
Дано: АВСD

описан около окружности,
АВ = 8, ВС = 12, СD = 13.
Найти: АD.

Решение:

АD + ВС = АВ + СD, так как суммы
противоположных сторон описанного четырехугольника равны.

Ответ: 9.

2) АD + 12 = 8 + 13
АD = 21 – 12
АD = 9

Задача №9

Точки О и С лежат в одной полуплоскости относительно

прямой АВ. Найдите угол АСВ, если угол АОВ равен 73°.

Дано: треугольник АВС вписан в
окружность, ∠АОВ = 73°.
Найти: ∠АСВ.

Решение:

∠ АОВ = 73° – центральный угол, опирающийся на ᴗ АВ, следовательно ᴗ АВ = 73°.

Ответ: 36,5.

2) ∠АСВ = 73° : 2 = 36, 5° , так как вписанный
угол измеряется половиной дуги, на которую он
опирается.

Задача №10

Найти высоту этой трапеции.

Дано: трапеция вписана в окружность, r

= 12.

Найти: h.
Решение:
Высота трапеции равна диаметру вписанной
окружности, поэтому h = 2  r = 2  12 = 24 .

Ответ: 24.

описанной около него окружности . Найдите ∠ А, если

∠В = 44°. Ответ дайте в градусах.

Дано: треугольник АВС вписан в окружность,
∠В = 44 °.
Найти: ∠А.
Решение:
1)∠C = 90°, так как угол, опирающийся на диаметр, значит треугольник АВС прямоугольный.
2)По теореме о сумме углов треугольника
∠А = 180° – (90° + 44°) = 46°
Ответ: 46.

равен 37°, а угол САD равен 58°. Найдите угол

АВС. Ответ дайте в градусах.

Дано: АВСD вписан в окружность,
∠АВD = 37°, ∠САD = 58°.
Найти: ∠АВС.
Решение:

2) ∠САD = 58° – вписанный угол, опирающийся на ᴗ СD,
поэтому ᴗ СD = 58°  2 = 116°.
ᴗ АDС = ᴗ АD + ᴗ DС = 74° + 116° = 190°,
значит ∠АВС = 190° : 2 = 95°.
Ответ: 95.

∠АВD = 37° – вписанный угол, опирающийся на ᴗ АD,
поэтому ᴗ АD = 37°  2 = 74°.

около равнобедренного треугольника АВС, в котором АВ = ВС

и ∠АВС = 107°. Найдите величину угла ВОС. Ответ дайте в градусах.

Дано: АВС вписан в окружность,
АВ = ВС, ∠АВС = 107°.
Найти: ∠ВОС.
Решение:
1)Треугольник АВС равнобедренный, поэтому в нем углы при основании равны, то есть
∠А = ∠АСВ = (180° – 107°) : 2 = 36,5°.
2)∠ВАС = 36,5° – вписанный угол, опирающийся на ᴗ ВС, поэтому ᴗ ВС = 36,5°  2 = 73°.
3)∠ ВОС – центральный угол, опирающийся
на ᴗ ВС, следовательно ∠ ВОС = ᴗ ВС = 73°.
Ответ: 73.

6.
Найдите высоту этого треугольника.

Дано: треугольник АВС описан около

окружности, r = 6.
Найти: h.
Решение:
1) В равностороннем треугольнике любая высота является медианой и биссектрисой и все они пересекаются в одной точке, которая является центром вписанной и описанной окружности.
2) Медианы треугольника точкой пересечения делятся в отношении 2: 1, считая от вершины,
значит h = 6  3 = 18.
Ответ: 18.

две прямые. Одна прямая касается окружности в точке К.

Другая прямая пересекает окружность в точках В и С, причем АВ = 2, АК = 4. Найдите АС.

Дано: АК – касательная, АС – секущая,
АВ = 2, АК = 4
Найти: АС.
Решение:
АК2 = АВ  АС
42 = 2  АС
АС = 16 : 2
АС = 8
Ответ: 8.