подъема, высоту подъема;
-определить дальность полета, модуль вектора скорости в
любой момент времени;
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть













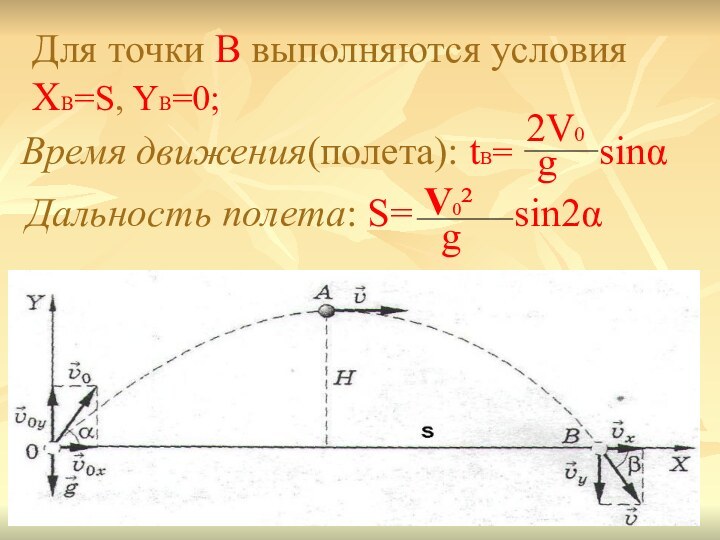






X=V0cosα·t
Vx=const
Vx=V0cosα
X=Vxt
при X0=0
Y=Y0+V0y·t+gy·t²/2
Y0=0
gy= - g
Y=V0sinα·t-gt²/2
Vy=V0sinα-gt
Vy=V0y+gyt
V0y=V0sinα
cosα
x
V0cosα
x
Или y=ax-bx²
Y(x) является ПАРАБОЛОЙ