Презентация на тему Меры связи, основанные на статистической зависимости. Коэффициент Юла

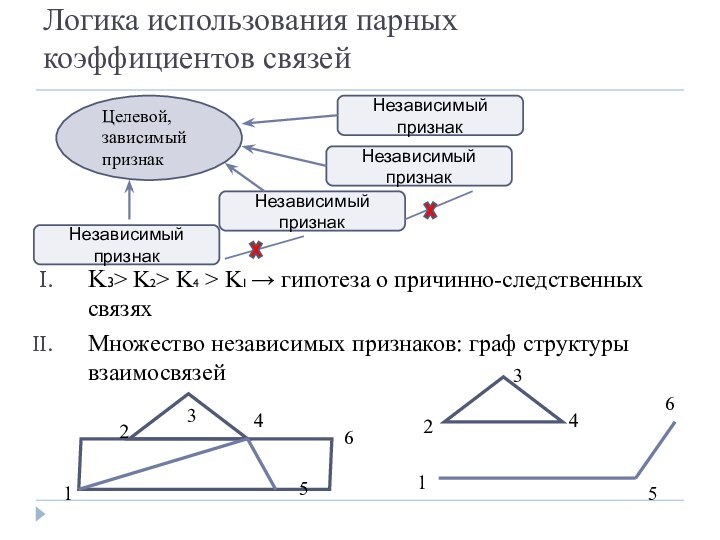
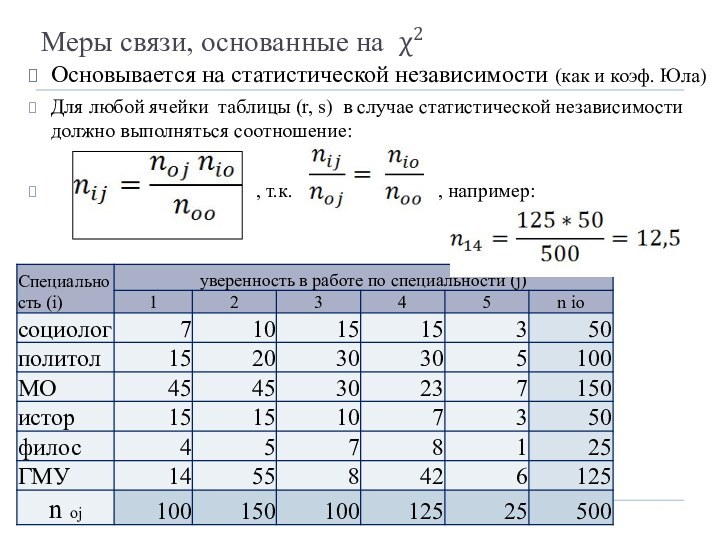
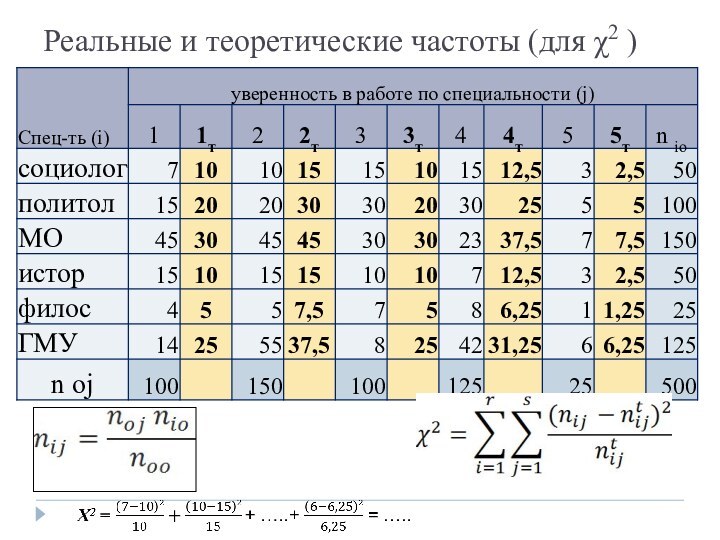
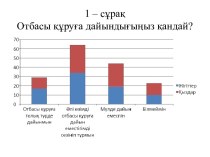
K1 → гипотеза о причинно-следственных связях
Множество независимых признаков: граф

структуры взаимосвязей

Целевой,
зависимый
признак

Независимый признак

Независимый признак

Независимый признак

Независимый признак

2

1

1

2

3

3

4

4

5

5

6

6

социологи
Есть ли статистическая закономерность между этими признаками?
Если наблюдается

статистическая независимость, то …
доля магистров в группе «уверенных» должна равняться доле магистров в группе «неуверенных», т.е.


, т.е. a (d+b) = (a+c) d → ab = cd ; и a (c + b) = (a + d) c → ab = cd
ab - cd - мера отклонения от статистической независимости;
Знаменатель – для нормирования (изменения от – 1 до + 1)

Коэффициент Юла:

0 или d = 0

Q = - 1,

если а = 0 или b = 0

Q = 0, если ab = cd,

т.е. наблюдается статистическая независимость

Q = 0,1397 ~ 0,14

Qп= 0,14; Qмо= - 0,35; Qис= -

0,29; Qф= 0,14; Qгму= 0,25

0,14;
Qмо= - 0,35;
Qис= - 0,29;
Qф= 0,14;

Qгму= 0,25
Коэффициенты упорядочиваются по силе связи (без учета прямая или обратная зависимость), т.о.:
Qмо > Qис > Qгму > Qс > Qп > Qф

Связь (в данном контексте) – статистическая зависимость

- правило детерминации:
одно свойство оказывает влияние на другое: А

→ В.
Например: Социолог → Уверенность в работе.
Характеристики детерминации:
Интенсивность : Емкость:


Для социологов: а = 18; a + d = 50; a + c = 150
I (C →У) = 36 %, С (С→ У) = 12 %
Интерпретация детерминации (схема):

независимость
для всех для девушек

для юношей







Qс= 0,15 – ложное отсутствие корреляционной связи

4

3

2

1

5

6

(как и коэф. Юла)
Для любой ячейки таблицы (r, s)

в случае статистической независимости должно выполняться соотношение:

, т.к. , например:

– табличное значение коэффициента (находим по таблице, при заданном

уровне значимости (возможной ошибки α =0,1; 0,05;0,01) и числе степеней свободы (r-1) (s-1) (где r – число строк, s – число столбцов в таблице)
ВЫВОД о статистической значимости: Если χ2 > χ2t при заданном уровне значимости (возможной ошибки α =0,1; 0,05;0,01) и числе степеней свободы (r-1) (s-1) – признаки являются статистически зависимыми…
Наиболее часто используемый коэффициентов на основе распределения χ2 :



С – приближается к 0 или 1

локальные связи на основе использования коэффициента Юла. Описать результаты

Вычислить интенсивность и емкость детерминации для нескольких свойств (в этом же примере). Описать результаты.
Вычислить значение хи-квадрат и сравнить с табличным при различных уровнях значимости (НАЙТИ ТАБЛИЦУ ХИ-КВАДРАТ САМОСТОЯТЕЛЬНО). Описать результаты