Слайд 3
2. Определенный интеграл
2.11. Некоторые применения определенного интеграла
2.11.1. Длина
дуги гладкой кривой
Определение. Множество {М} всех точек
М, координаты х и у которых
определяются уравнениями
x = (t); y = (t); (t), (t) C[a; b],
будем называть простой плоской кривой L, если различным значениям параметра t из отрезка [а, b] отвечают различные точки этого множества.
Строфоида
Слайд 4
2.11.1. Длина дуги гладкой кривой
Пусть Т —
произвольное разбиение
Сегмента [а, b] точками
а = t0
< t1 < t2 < … < tn = b.
Обозначим M0, M1, M2, ... , Mn
соответствующие точки кривой L.
Возникающую при этом ломаную
M0M1M2 ... Мn будем называть ломаной),
вписанной в кривую L и отвечающей
данному разбиению Т отрезка [а, b]. Так
как длина звена Мi -1Мi этой ломаной
равна
то длина всей этой ломаной равна
Слайд 5
2.11.1. Длина дуги гладкой кривой
Определение. Если множество

длин вписанных в кривую L ломаных, отвечающих всевозможным разбиениям
Т отрезка [а, b], ограничено, то кривая L называется спрямляемой, а точная верхняя грань l этого множества называется длиной дуги кривой L.
Лемма. Пусть l(T*) — длина ломаной, вписанной в кривую L и отвечающей разбиению Т* отрезка [а, b], а l(T) - длина ломаной, вписанной в кривую L и отвечающей разбиению Т, полученному из разбиения Т* посредством добавления нескольких новых точек. Тогда l(T*) l(T).
Свойства спрямляемой кривой.
1°. Если кривая L спрямляема, то длина l ее дуги не зависит от параметризации этой кривой.
2°. Если спрямляемая кривая L разбита при помощи конечного числа точек M0, М1, …, Мn, на конечное число кривых Li, то каждая из этих кривых Li спрямляема и сумма длин li всех кривых Li равна длине l кривой L.
3°. Пусть кривая L задана параметрически уравнениями, приведенными выше. Обозначим l(t) длину дуги участка Lt кривой L, точки которого определяются всеми значениями параметра из отрезка [а, b]. Функция l(t) является возрастающей и непрерывной функцией параметра t. Эту функцию l(t) будем называть переменной дугой на кривой L.
4°. Переменная дуга l(t) может быть выбрана в качестве параметра. Этот параметр называется натуральным параметром.
Слайд 8
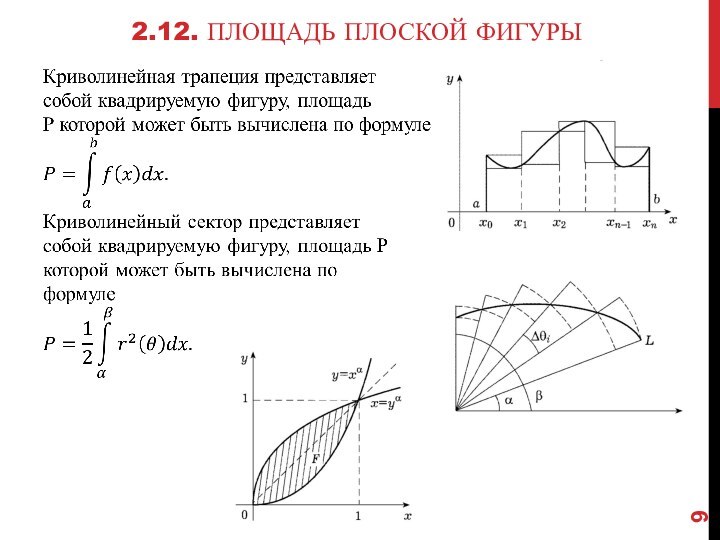
2.12. Площадь плоской фигуры
Определение. Плоская фигура Q
— часть плоскости, ограниченной простой замкнутой кривой.
Многоугольник вписан в
фигуру Q, если каждая точка этого многоугольника принадлежит фигуре Q или ее границе. Если все точки плоской фигуры и ее границы принадлежат некоторому многоугольнику, то будем говорить, что указанный многоугольник описан вокруг фигуры Q.
P* = sup Si; P* = inf Sd
Определение. Плоская фигура Q называется квадрируемой, если верхняя площадь P* этой фигуры совпадает с ее нижней площадью P*. При этом число Р = P* = P* называется площадью фигуры Q.
Теорема. Для того чтобы плоская фигура Q была квадрируемой, необходимо и достаточно, чтобы для любого положительного числа > 0 можно было указать такой описанный вокруг фигуры Q многоугольник и такой вписанный в фигуру Q многоугольник, разность Sd — Si площадей которых была бы меньше : Sd — Si < .