многоугольник составлен из нескольких многоугольников, то его площадь равна
сумме площадей этих многоугольников:3. Площадь квадрата равна квадрату его стороны:
Далее…
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике 5 класс Деление десятичных дробей
Содержание
- 2. Свойства площадей1. Равные многоугольники имеют равные площади:2.
- 3. Площадь прямоугольникаТеорема: Площадь прямоугольника равна произведению его
- 4. Теорема: Площадь параллелограмма равна произведению его основания
- 5. Площадь треугольникаТеорема: Площадь треугольника равна половине произведения
- 6. СледствияСледствие 1: Площадь прямоугольного треугольника равна половине
- 7. Площадь трапецииТеорема: Площадь трапеции равна произведению полусуммы
- 8. Теорема: Если угол одного треугольника равен углу
- 9. Скачать презентацию
- 10. Похожие презентации
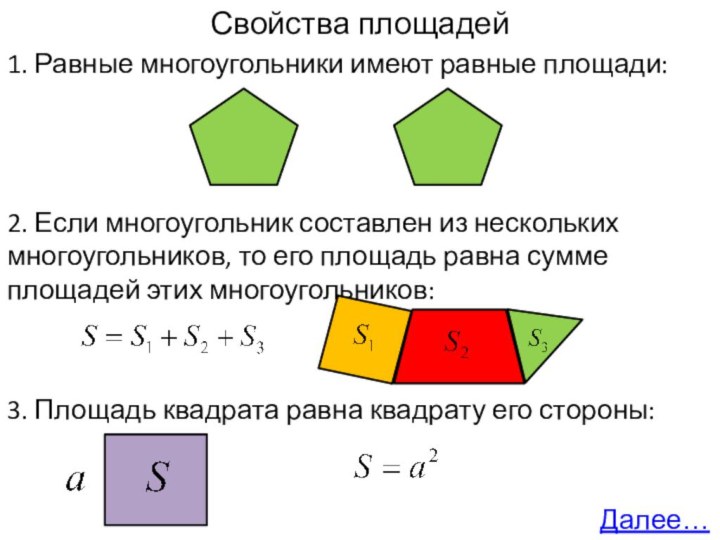
Свойства площадей1. Равные многоугольники имеют равные площади:2. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников:3. Площадь квадрата равна квадрату его стороны:Далее…
Слайд 2
Свойства площадей
1. Равные многоугольники имеют равные площади:
2. Если
Слайд 3
Площадь прямоугольника
Теорема: Площадь прямоугольника равна произведению его смежных
сторон.
Дано: Прямоугольник
Стороны равны a, b
Площадь равна S
Доказать: S =
ab1. Достроим прямоугольник до квадрата со стороной a + b
3. Площадь большого квадрата по свойству площадей 3:
4. И по свойству площадей 2:
2. Площади получившихся квадратов будут равны:
5. Так как равны левые части равенств, то должны быть равны и правые части равенств:
Далее…
Слайд 4 Теорема: Площадь параллелограмма равна произведению его основания на
высоту.
Площадь параллелограмма
Дано:
ABCD – параллелограмм
AD – основание
BH
- высотаПлощадь равна S
Доказать:
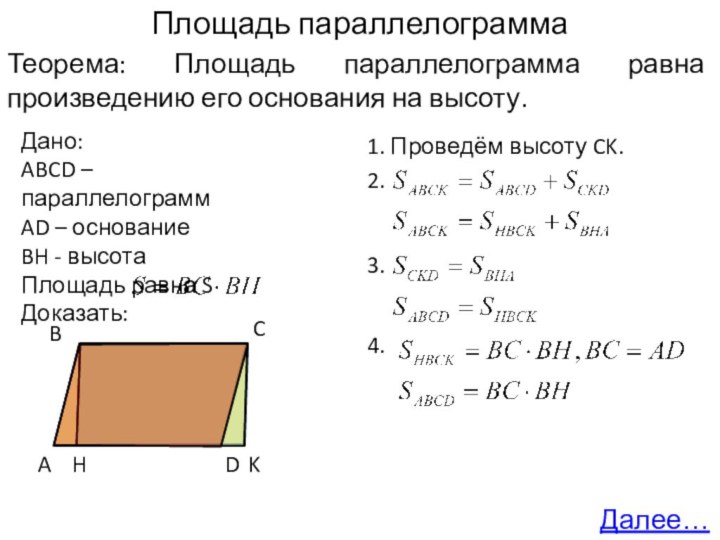
1. Проведём высоту CK.
2.
3.
4.
A
B
C
D
H
K
Далее…
Слайд 5
Площадь треугольника
Теорема: Площадь треугольника равна половине произведения основания
на высоту, опущенную к этому основанию.
Дано:
ABC – треугольник
AB – основание
CH - высота
Площадь равна S
Доказать:
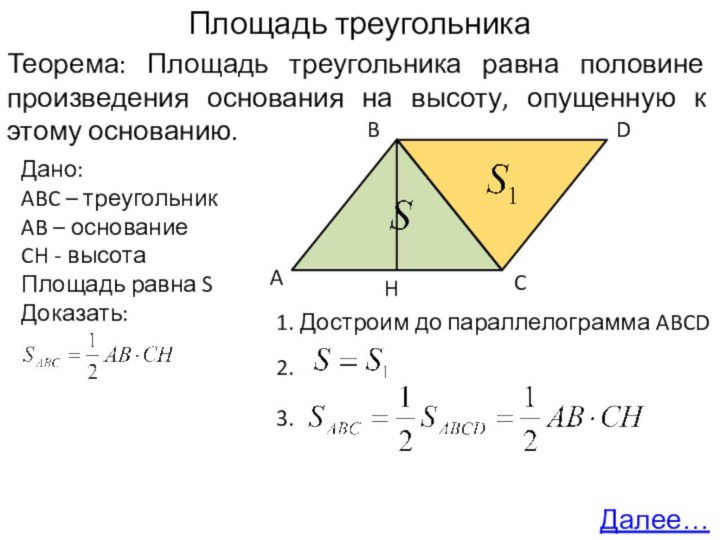
1. Достроим до параллелограмма ABCD
2.
3.
A
B
C
D
H
Далее…
Слайд 6
Следствия
Следствие 1: Площадь прямоугольного треугольника равна половине произведения
его катетов.
Следствие 2: Если высоты двух треугольников равны, то
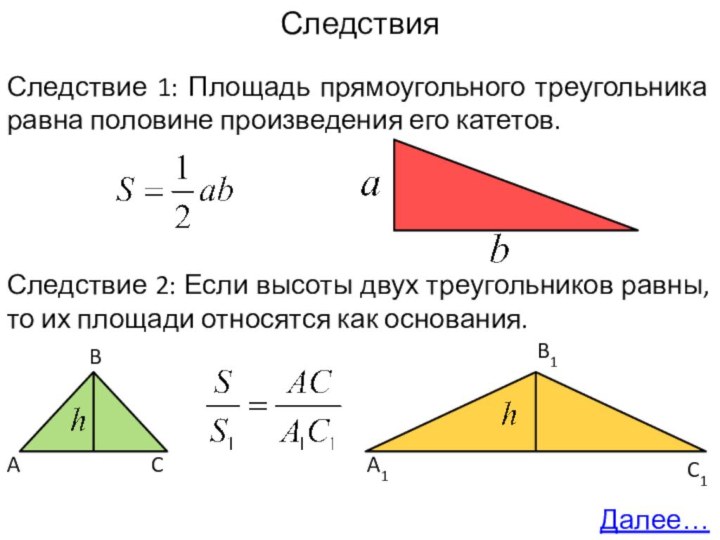
их площади относятся как основания.A
B
C
A1
B1
C1
Далее…
Слайд 7
Площадь трапеции
Теорема: Площадь трапеции равна произведению полусуммы её
оснований на высоту.
Дано: ABCD – трапеция
AD, BC
– основанияBH – высота
Площадь равна S
Доказать:
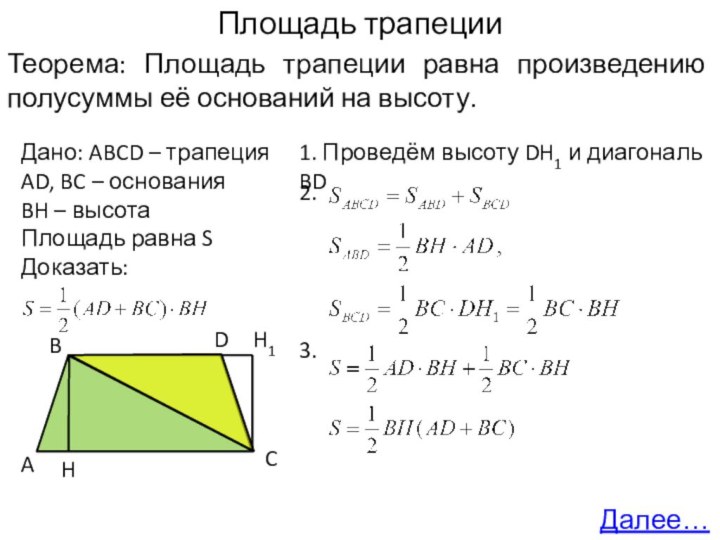
1. Проведём высоту DH1 и диагональ BD
2.
3.
A
B
C
D
H
H1
Далее…
Слайд 8 Теорема: Если угол одного треугольника равен углу другого
треугольника, то площади этих треугольников относятся как произведения сторон,
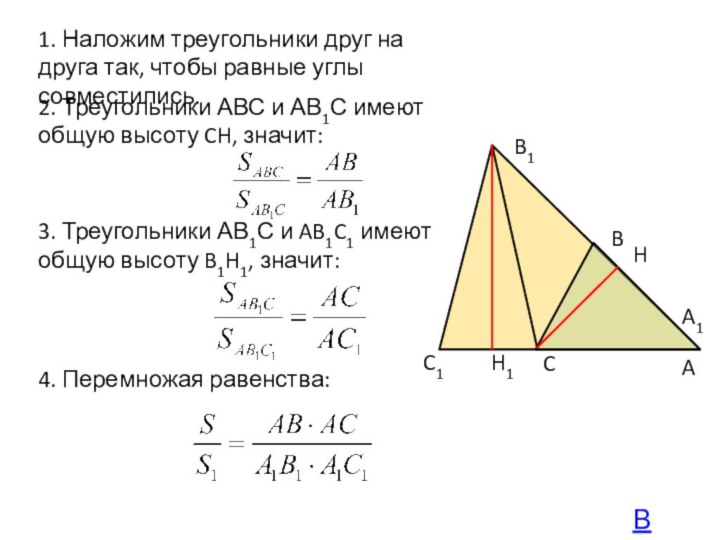
заключающих равные углы.Дано: ABC и A1B1C1 – треугольники
Угол А равен углу A1
Площади равны S и S1
соответственно
Доказать:
A
B
C
A1
B1
C1
Далее…
