Слайд 2
Оглавление
1.1 ТОЧКА
Проецирование точки на плоскости проекций
Точка на
комплексном чертеже
1.2 ПРЯМАЯ
Следы прямой
Определение истинной величины отрезка прямой и
углов наклона прямой к плоскостям проекций
1.3 ПЛОСКОСТЬ
Следы плоскости
Пересечение двух плоскостей
Плоскости общего положения
Геометрические фигуры
Точка встречи прямой с плоскостью общего положения , определение видимости прямой относительно плоскости
2 ГЕОМЕТРИЧЕСКИЕ ТЕЛА
Пересечение прямой с геометрическими телами
3 ЗАДАЧИ
Слайд 4
Построить проекции точек с координатами:
x
z
y
y
A (x; y; z)
z=0
A2
A1
A3
ax
az
ay
ay
o
Слайд 5
Построить проекции точек с координатами:
x
z
y
y
A (x; y; z)
z=0
A2
A1
A3
ax
az
ay
ay
o
Слайд 6
Построить проекции точек с координатами:
x
z
y
y
A (x; y; z)
y=0
A2
A1
A3
ax
az
ay
ay
o
Слайд 7
Построить проекции точек с координатами:
x
z
y
y
A (x; y; z)
y=0
A2
A1
A3
ax
az
ay
ay
o
Слайд 8
Построить проекции точек с координатами:
x
z
y
y
A(x; y; z) x=0
A2
A1
A3
ax
az
ay
ay
o
Слайд 9
Построить проекции точек с координатами:
x
z
y
y
A (x; y; z)
x=0
A2
A1
A3
ax
az
ay
ay
o
назад
назад
далее
Слайд 10
Точка на комплексном чертеже
Точка на комплексном чертеже
Слайд 11
Построить проекции точек с координатами:
x
z
y
y
A(x; y; z)
A2
A1
A3
ax
az
ay
ay
o
Слайд 12
Построить проекции точек с координатами:
x
z
y
y
A(x; y;z)
A2
A1
A3
ax
az
ay
ay
o
Слайд 13
Построить проекции точек с координатами:
x
z
y
y
B(x; -y;z)
B2
B1
B3
bx
bz
by
by
-y
-y
-z
-x
o
Слайд 14
Построить проекции точек с координатами:
x
z
y
y
B(x; -y;z)
B2
B1
B3
bx
bz
by
by
-y
-y
-z
-x
o
Слайд 15
Построить проекции точек с координатами:
x
z
y
y
C(x; -y;-z)
C2
C1
C3
cx
cz
cy
cy
-y
-y
-z
-x
o
Слайд 16
Построить проекции точек с координатами:
x
z
y
y
C(x; -y;-z)
C2
C1
C3
cx
cz
cy
cy
-y
-y
-z
-x
o
Слайд 17
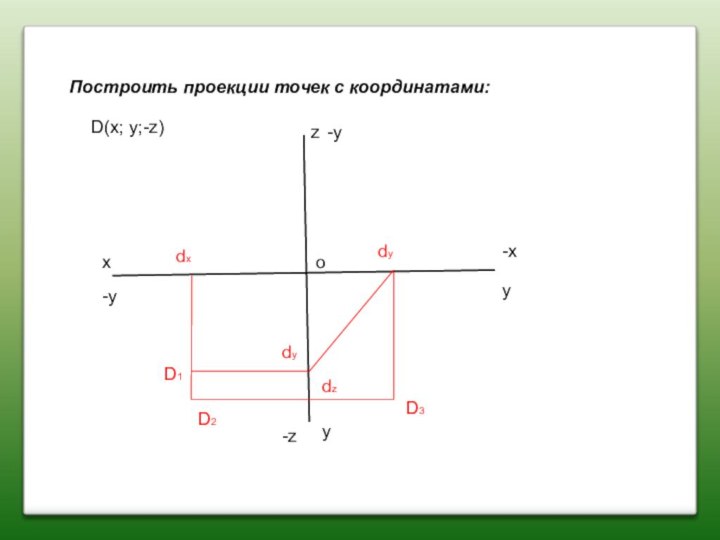
Построить проекции точек с координатами:
x
z
y
y
D(x; y;-z)
D2
D1
D3
dx
dz
dy
dy
-y
-y
-z
-x
o
Слайд 18
Построить проекции точек с координатами:
x
z
y
y
D(x; y;-z)
D2
D1
D3
dx
dz
dy
dy
-y
-y
-z
-x
o
Слайд 19
Построить проекции точек с координатами:
x
z
y
y
E(-x; y;z)
E2
E1
E3
ex
ez
ey
ey
-y
-y
-z
-x
o
Слайд 20
Построить проекции точек с координатами:
x
z
y
y
E(-x; y;z)
E2
E1
E3
ex
ez
ey
ey
-y
-y
-z
-x
o
Слайд 21
Построить проекции точек с координатами:
x
z
y
y
F(-x;- y; z)
F2
F1
F3
fx
fz
fy
fy
-y
-y
-z
-x
o
Слайд 22
Построить проекции точек с координатами:
x
z
y
y
F(-x;- y;z)
F2
F1
F3
fx
fz
fy
fy
-y
-y
-z
-x
o
Слайд 23
Построить проекции точек с координатами:
x
z
y
y
G(-x;- y;-z)
G2
G1
G3
gx
gz
gy
gy
-y
-y
-z
-x
o
Слайд 24
Построить проекции точек с координатами:
x
z
y
y
G(-x;- y;-z)
G2
G1
G3
fx
gz
gy
gy
-y
-y
-z
-x
o
Слайд 25
Построить проекции точек с координатами:
x
z
y
y
S(-x;y;-z)
S2
S1
S3
sx
sz
sy
sy
-y
-y
-z
-x
o
Слайд 26
Построить проекции точек с координатами:
x
z
y
y
S(-x;y;-z)
S2
S1
S3
sx
sz
sy
sy
-y
-y
-z
-x
o
назад
назад
далее
Слайд 27
Точка на комплексном чертеже
Следы прямой
Слайд 28
ЗАДАЧА Построить следы прямой АВ, покапать видимость прямой,
дать характеристики положения прямой в пространстве относительно плоскостей проекций.
А2
А1
В2
В1
х
о
Слайд 29
А2
А1
В2
В1
х
о
2. Соединить одноименные
проекции точек и
определить горизонтальный след прямой - точку Н (Н2 H1)
Н2
Н 1
Слайд 30
А2
А1
В2
В1
х
о
2. Определить фронтальный след прямой АВ - точку
F (F2,F1)
Н2
Н 1
F2
F1
Слайд 31
А2
А1
В2
В1
х
о
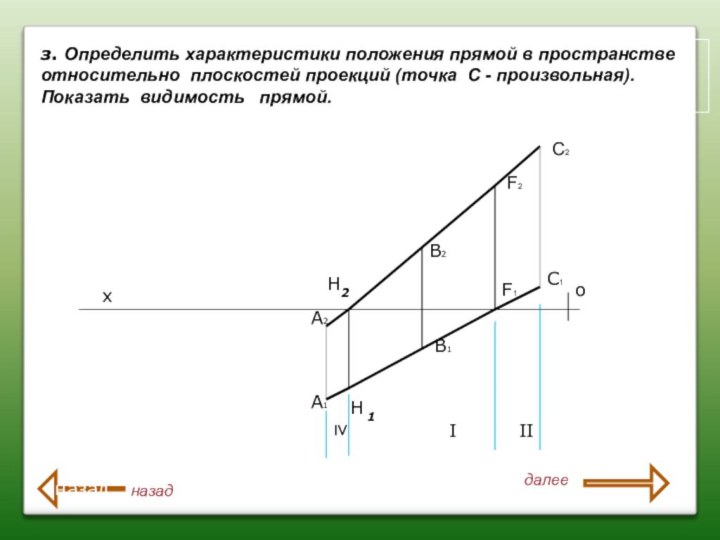
з. Определить характеристики положения прямой в пространстве
относительно плоскостей проекций (точка С - произвольная).
Показать видимость
прямой
Н2
Н 1
F2
F1
Слайд 32
А2
А1
В2
В1
х
о
з. Определить характеристики положения прямой в пространстве
относительно плоскостей проекций (точка С - произвольная).
Показать видимость
прямой.
Н2
Н 1
F2
F1
С1
С2
Ι
≥
ΙΙ
назад
назад
далее
Слайд 33
Точка на комплексном чертеже
Определение истинной величины отрезка прямой
и углов наклона прямой к плоскостям проекций
Слайд 34
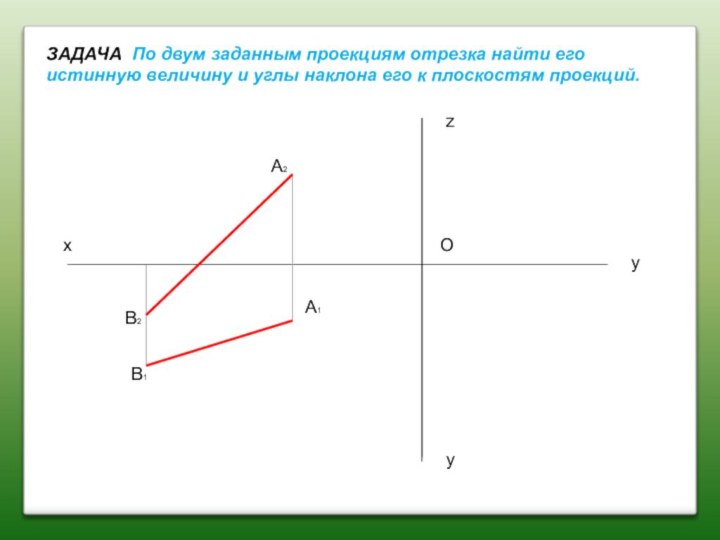
ЗАДАЧА По двум заданным проекциям отрезка найти его
истинную величину и углы наклона его к плоскостям проекций.
О
х
у
z
y
А1
А2
В1
В2
Слайд 35
1. Построить профильную проекцию заданного отрезка А В
О
х
у
z
y
А1
А2
В1
В2
А3
В3
Слайд 36
2. Определить следы отрезка и показать видимость его.
О
х
у
z
y
А1
А2
В1
В2
А3
В3
Н2
Н1
Н3
Н3
Слайд 37
3. Определить графи чески алгебраическую разность координат концов
заданного отрезка: х = хв - хА У
= Ув - УА Z = ZA - Zв
О
х
у
z
y
А1
А2
В1
В2
А3
В3
Н2
Н1
Н3
Δх
Δ у
Δ z
Н3
Слайд 38
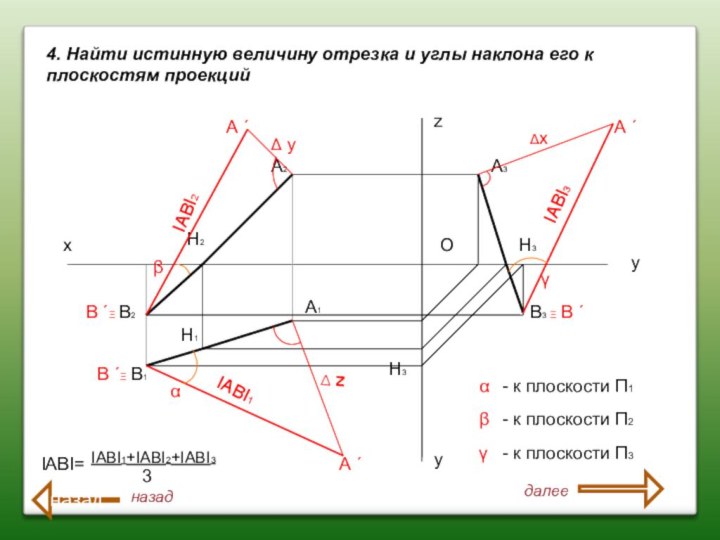
4. Найти истинную величину отрезка и углы наклона
его к плоскостям проекций
О
х
у
z
y
А1
А2
В1
В2
А3
В3
Н2
Н1
Н3
В ´Ξ
В ´Ξ
Ξ В
´
А ´
А ´
А ´
ΙАВΙ1
ΙАВΙ3
ΙАВΙ2
Δх
Δ z
Δ у
β
α
γ
α
β
γ
- к плоскости П1
- к плоскости П2
- к плоскости П3
ΙАВΙ=
ΙАВΙ1+ΙАВΙ2+ΙАВΙ3
3
Н3
назад
назад
далее
Слайд 39
Точка на комплексном чертеже
Следы плоскости
Слайд 40
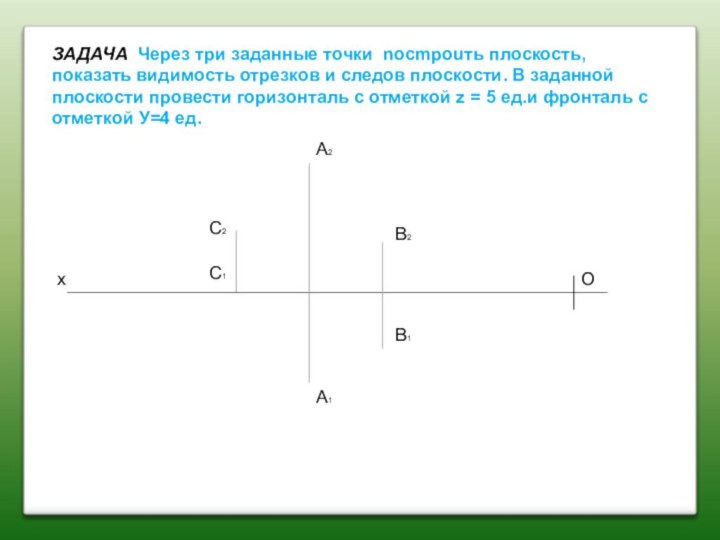
ЗАДАЧА Через три заданные точки nоcmроuть плоскость, показать
видимость отрезков и следов плоскости. В заданной плоскости провести
горизонталь с отметкой z = 5 ед.и фронталь с отметкой У=4 ед.
О
х
С2
С1
А2
А1
В2
В1
Слайд 41
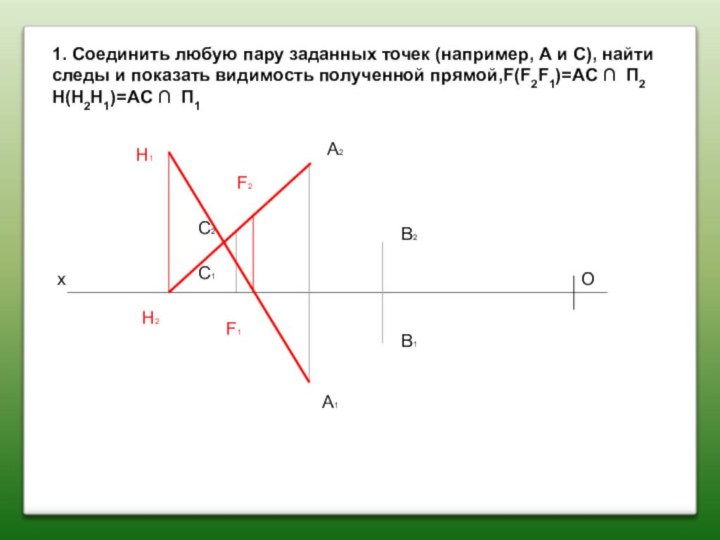
1. Соединить любую пару заданных точек (например, А
и С), найти следы и показать видимость полученной прямой,F(F2F1)=AC
∩ П2 H(H2H1)=AC ∩ П1
О
х
С2
С1
А2
А1
В2
В1
F1
F2
Н2
Н1
Слайд 42
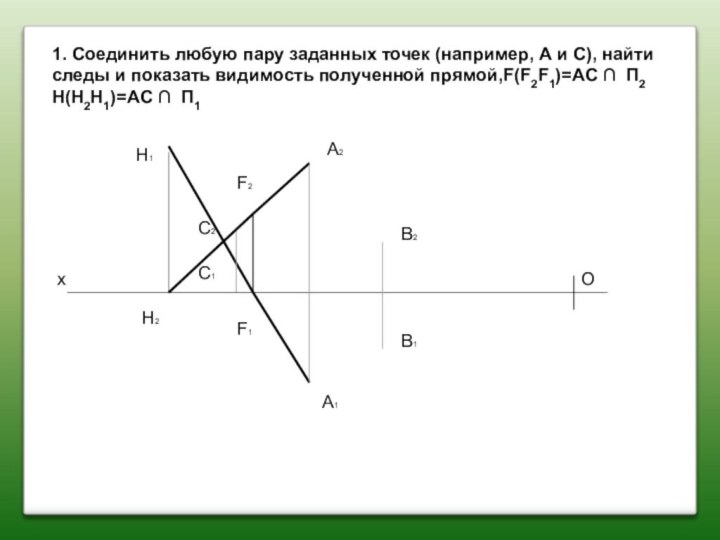
1. Соединить любую пару заданных точек (например, А
и С), найти следы и показать видимость полученной прямой,F(F2F1)=AC
∩ П2 H(H2H1)=AC ∩ П1
О
х
С2
С1
А2
А1
В2
В1
F1
F2
Н2
Н1
Слайд 43
2. Соединить другую пару заданных точек (например, А
и В), найти также следы и показamь видимость этой
прямой F1(F21,F11)=АB ∩ П2 H1(H21,H11)=АВ ∩ П1
О
х
С2
С1
А2
А1
В2
В1
F1
F2
Н2
Н1
Н11
Н21
F11
F21
Слайд 44
2. Соединить другую пару заданных точек (например, А
и В), найти также следы и показamь видимость этой
прямой F1(F21,F11)=АB ∩ П2 H1(H21,H11)=АВ ∩ П1
О
х
С2
С1
А2
А1
В2
В1
F1
F2
Н2
Н1
Н11
Н21
F11
F21
Слайд 45
3. Через следы прямых провести соответствующие следы плоскости
FF1= f o а Н Hi = hoа
Следы плоскостей должны пересекаться на оси 0х ; Х а = hо а ∩ fо а ; Ха Є Ох
О
х
С2
С1
А2
А1
В2
В1
F1
F2
Н2
Н1
Н11
Н21
F11
F21
hо а
fо а
Ха
Слайд 46
4 Показать видимость следов плоскости
foa - всегда видны
выше оси Ох
h0а - всегда видны ниже оси Ох
О
х
С2
С1
А2
А1
В2
В1
F1
F2
Н2
Н1
Н11
Н21
F11
F21
fо
а
Ха
hо а
Слайд 47
5. Пpoвecmu горизонталь плоскости 1 2 (1222,1121) с
отметкой z=5 1222|| Ох 1121|| h0a
О
х
С2
С1
А2
А1
В2
В1
F1
F2
Н2
Н1
Н11
Н21
F11
F21
fо
а
Ха
hо а
Ι Ι
Ι Ι
z=5
12
11
22
21
Слайд 48
6. Провесmи фронталь плоскости 34(3242;3141) С отметкой у=4
3141 || 0х 3242
|| foа
О
х
С2
С1
А2
А1
В2
В1
F1
F2
Н2
Н1
Н11
Н21
F11
F21
fо а
Ха
hо а
12
11
22
21
у=4
31
32
41
42
К2
К1
Проверка:
горизонталь и фронталь должны пересечься в одной точке К (К2 К1) К (К2К1) = 12 ∩ 34
назад
назад
далее
Слайд 49
Точка на комплексном чертеже
Пересечение двух плоскостей
(плоскости общего положения)
Слайд 50
Задача Построить линию пересечения 2-х плоскостей заданных следами,
когда следы плоскостей пересекаются в пределах чертежа, Дать харак-теристику
положения линии пересечения в пространстве относительно плоскостей проекций. Показать видимость следов плоскостей и линии пересечения
х
о
foa
foв
hoв
hoa
Слайд 51
1.Пpoвecmu вспомогательную секущую плоскость γ II П1 (произвольно)
х
о
foα
foβ
hoβ
hoα
foγ
Слайд 52
2. Определить линию пересечения плоскости α со вспомогamельной
плоскостью γ (это будет горизонталь плоскости α) α ∩
γ=MN
х
о
foα
foβ
hoβ
hoα
foγ
N2
N1
M1
M2
Слайд 53
3. Определить линию пересечения плоскости β со вспомoгательной
плоскостью γ (это будет горизонталь плоскости γ), β ∩
γ =12
х
о
foα
foβ
hoβ
hoα
foγ
N2
N1
M1
M2
12
11
21
22
Слайд 54
4. Определить точку К(К2, К1) принадлежащую линии пересечения
плоскостей α и β NM ∩ 12=K
х
о
foα
foβ
hoβ
hoα
foγ
N2
N1
M1
M2
22
21
12
11
K1
K2
Слайд 55
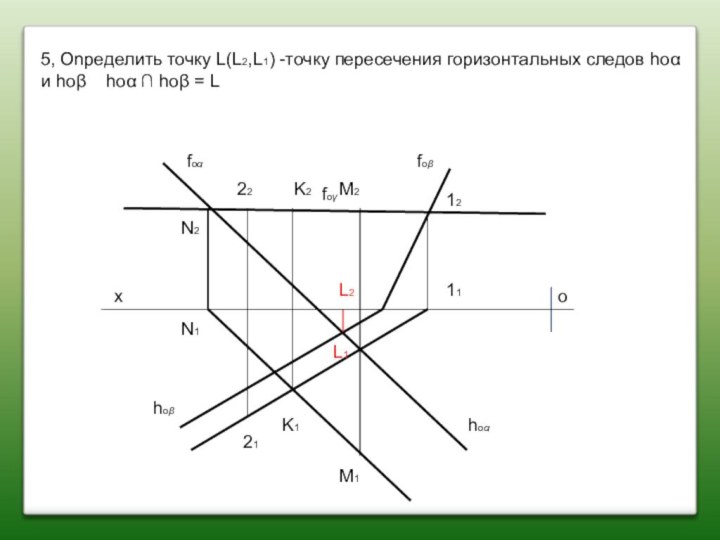
5, Onределить точку L(L2,L1) -точку пересечения горизонтальных следов
hoα и hoβ hoα ∩ hoβ = L
х
о
foα
foβ
hoβ
hoα
foγ
N2
N1
M1
M2
K2
22
21
K1
12
11
L2
L1
Слайд 56
6. Определить линию КL (К2L2, К1L1)-пересечения плоскостей α
и β
α ∩ β =KL
х
о
foα
foβ
hoβ
hoα
foγ
N2
N1
M1
M2
L2
L1
12
11
22
21
K2
K1
Слайд 57
7, Определить характеристику линии пересечения относительна плоскостей проекций(П1П2).
х
о
foα
foβ
hoβ
hoα
foγ
N2
N1
M1
M2
L2
L1
12
11
22
21
K2
K1
п. п.
н.п
KL- I -Пл.П1 – IV - Пл.П2 - III
назад
назад
далее
Слайд 58
Точка на комплексном чертеже
Пересечение двух плоскостей
(Заданных геометрическими
фигурами )
Слайд 59
x
o
A2
A1
D1
D2
B2
B1
C2
C1
E2
E1
K2
K1
Задача: Построить линию пересечения двух плоскостей, заданных плоскими
фигурами:Δ АВС и Δ ДКЕ показать видимость.
Слайд 60
x
o
A2
A1
D1
D2
B2
B1
C2
C1
E2
E1
K2
K1
F1
F2
21
22
11
12
31
32
Воспользуемся вспомогательной секущей плоскостью βΙΙ П2 проходящей через(·)
А Δ АВС эта плоскость пересечет Δ АВС по
фронтали А1(А212)
Δ АВС ∩β=А1 плоскость β пересекает Δ ДКЕ по фронтали2;3 Δ ДКЕ ∩β= 23
Точка пересечения фронталей А1 и 23 даёт искомую (·) F = А1 ∩ 23
Слайд 61
x
o
A2
A1
D1
D2
B2
B1
C2
C1
E2
E1
K2
K1
F1
F2
21
22
11
12
31
32
41
51
51
41
f
h
x
R2
R1
2. Для получения второй точки линии пересечения Δ
АВС и Δ ДКЕ восполь-
зуемся плоскостью γ П1
и проходящей через сторону КЕ Δ ДКЕ
Δ ДКЕ ∩ γ =КЕ Δ АВС ∩ γ=45 КЕ ∩ 45= (·)R(R2R1)
Т
Слайд 62
x
o
A2
A1
D1
D2
B2
B1
C2
C1
E2
E1
K2
K1
F1
F2
21
22
11
12
31
32
41
51
51
41
f
h α
xα
R2
R1
3. Соединив одноименные проекции точек F
u R, получим проекции линии пересечения плоскостей Δ АВС
∩ Δ ДКЕ =FR
Слайд 63
x
o
A2
A1
D1
D2
B2
B1
C2
C1
E2
E1
K2
K1
F1
F2
21
22
11
12
31
32
41
51
51
41
f
h α
xα
R2
R1
4. Пользуясь методом конкурирующих точек, определяем видимость
заданных плоскостей относительно друг друга
Слайд 64
x
o
A2
A1
D1
D2
B2
B1
C2
C1
E2
E1
K2
K1
F1
F2
21
22
11
12
31
32
41
51
51
41
f α
h α
xα
R2
R1
5. Даем характеристику найденной линии пересечения
относительно плоскостей проекций.
.(FR) – I – пл.П2 – II
– пл.П1 - III
назад
назад
далее
Слайд 65
Точка на комплексном чертеже
Точка встречи прямой с плоскостью
общего положения , определение видимости прямой относительно плоскости
Слайд 66
Задача: определить точку пересечения прямой EF с плоскостью
, заданной плоскостью фигуры - треугольником АВС показать видимость
х
о
А2
A1
F2
F1
B2
B1
C1
C2
E2
E1
Слайд 67
1. Через EF провести
плоскость α П1,
hоa совпадает с Е1 F1 fоa Ox.
х
о
А2
A1
F2
F1
B2
B1
C1
C2
E2
E1
x
α
f α
h α
Т
Т
Слайд 68
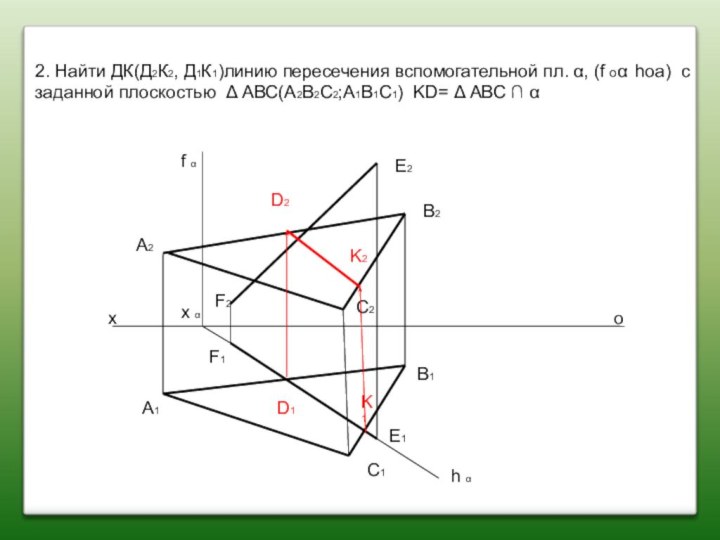
2. Найти ДК(Д2К2, Д1К1)линию пересечения вспомогательной пл. α,
(f оα hoa) с заданной плоскостью Δ АВС(А2В2С2;А1В1С1) KD=
Δ АВС ∩ α
х
о
А2
A1
F2
F1
B2
B1
C1
C2
E2
E1
x α
f α
h α
D1
K1
K2
D2
Слайд 69
3 Найти (•)М(M2M1) -(•) пересечения линии ДК
(Д2К2)(Д1К1) и прямой EF(E2F2; E1F1) (•) M=DК∩EF
.
х
о
А2
A1
F2
F1
B2
B1
C2
C1
E2
E1
x α
f
α
h α
D1
K1
K2
D2
M2
M1
Слайд 70
4. Используя конкурирующие точки 1(1211) 2(2221) Определить видимость.ΔАВС
представляет собой плоскость односторонней видимости, поэтому один и тот
же участок заданной прямой будет виден сверху(М1Е1)и спереди (M2Е2)
.
х
о
А2
A1
F2
F1
B2
B1
C2
C1
E2
E1
x α
f α
h α
D1
K1
K2
D2
M2
M1
Слайд 71
х
о
А2
A1
F2
F1
B2
B1
C2
C1
E2
E1
x α
f α
h α
D1
K1
K2
D2
M2
M1
5. Показываем видимость
назад
назад
далее
Слайд 72
Точка на комплексном чертеже
Пересечение прямой с геометрическими телами
Слайд 73
S2
S1
T2
T1
F2
F1
X
O
A2
A1
C2
C1
B2
B1
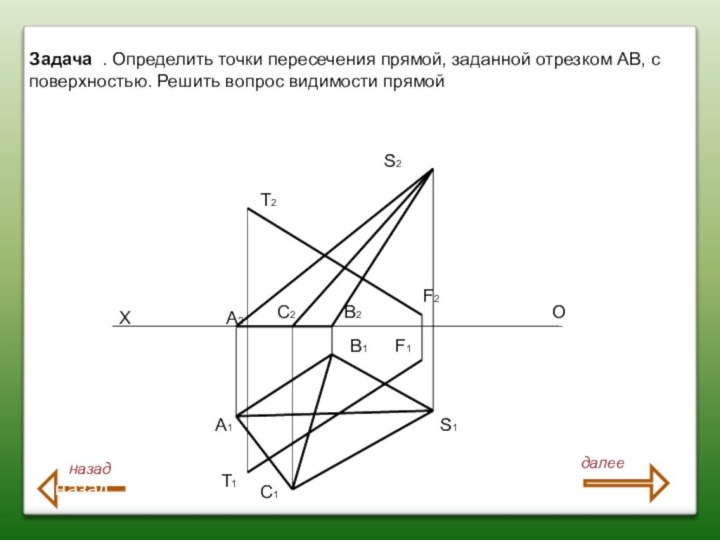
Задача : Построить точку пересечения прямой линии TF
с поверхностью многогранника. Показать видимость ребер многогранника секущей
прямой линии.
Слайд 74
S2
S1
T2
T1
F2
F1
X
O
A2
A1
C2
C1
B2
B1
1. Определяем видимость ребер многогранника, используя правило видимости
и метод конкурирующих точек 1(1211)2(2221).
Слайд 75
S2
S1
T2
T1
F2
F1
X
O
A2
A1
C2
C1
B2
B1
fOα
hOα
Xα
2. Через прямую ТF проводим вспомогательную
плоскосmь α , перпендикулярную фронтальной плоскости проекций П2: след
f0 α совпадает с Т2 F2 hOα оcu Ox.
Т
Слайд 76
S2
S1
T2
T1
F2
F1
X
O
A2
A1
C2
C1
B2
B1
fOα
hOα
Xα
12
22
32
11
21
31
3. Строим линию пересечения вспомогательной плоскости
α (fOα hOα) с поверхностью заданного многогранника фронтальная
проекция сечения плоскости α с поверхностью пирамиды (122232) совпала с фронтальным следом fOα плоскости α . гopuзонтальная проекция сечения 1121З1 определилась по точкам 1121З1 лежащим на соответствующих ребрах пирамиды ('построение показано стрелками),
Слайд 77
S2
S1
T2
T1
F2
F1
X
O
A2
A1
C2
C1
B2
B1
fOα
hOα
Xα
12
22
32
11
21
31
K1
R1
K1
R1
4. Найдем точки пересечения заданной пряной ТF с
контуром сечения 123 - точки К (К2
К1) и R(R2R1) По линиям связи отмечаем точки К2 и R2 на фронтальной проекции прямой Т2F2. Это и будут искомые точки (вxoдa и выxoдa) пересечения прямой с поверхностью многогранника (пирамиды).
Слайд 78
S2
S1
T2
T1
F2
F1
X
O
A2
A1
C2
C1
B2
B1
fOα
hOα
Xα
12
22
32
11
21
31
K1
R1
K1
R1
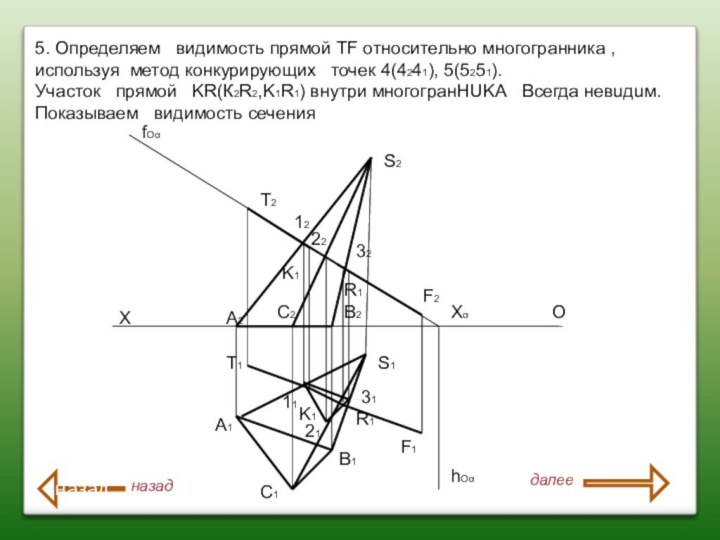
5. Определяем видимость прямой TF относительно многогранника
, используя метод конкурирующих точек 4(4241), 5(5251).
Участок
прямой KR(К2R2,K1R1) внутри многогранHUKА Всегда невuдuм.
Показываем видимость сечения
назад
назад
далее
Слайд 80
A2
A1
B2
B1
S2
S1
Задача: Определить точки пересечения прямой AВ с поверхностью
конуса. Показать видимость прямой.
Слайд 81
A2
A1
B2
B1
S2
S1
12
22
21
11
H12
H12
H22
H21
1 Через прямую АВ проводим вспомогательную плоскость. в
качестве вспомогательной плоскости принимаем плоскость, проходящую через вepшину
конуса S, и две точки 1и 2, произвольно взятые на прямой AВ. Определяем горизонтальные следы Н, (Н21,Н11) и
Н2(Н22Н21) пересекающихся прямых S1и S2. Точки 1и2 следует выбрать с таким расчетом, чтобы горизонтальные следы Н1 и H2 получились в пределах чертежа.
Слайд 82
A2
A1
B2
B1
S2
S1
11
21
12
22
31
32
41
42
H12
H12
H22
H22
ho α
2. Через гориз. следы прямых (н1 и
нг) проводим горизонтальный след ho α
плоскости α Так
как конус своим основанием расположен на плоскости, определяем точки 3 и 4 пересечения основания со следом
Слайд 83
A2
A1
B2
B1
S2
S1
11
21
12
22
31
32
41
41
H12
H12
H22
H22
ho α
S3 и S4 - образующие.
Слайд 84
A2
A1
B2
B1
S2
S1
11
21
12
22
31
32
41
41
H12
H12
H22
H22
K1
L1
L2
K2
ho α
3. Определяем линию пересечения вспомогательной плоскости
α
с конусом - это образующие S3 и S4.
Слайд 85
A2
A1
B2
B1
S2
S1
11
21
12
22
31
32
41
41
H12
H12
H22
H22
K1
L1
L2
K2
ho α
В пересечении образующих S3 И S4 с
заданной прямой определяем искомые
Точки.AВ ∩ S3 = К AВ
∩ S4 = L . Определяем видимость прямой линии AВ.
назад
назад
далее
Слайд 87
C2
C1
A2
A1
B2
B1
П2
П1
О
Х
Задача : 0пределить moчки пересечения прямой AВ
с поверхностью
сферы, показать видимость прямой.
Слайд 88
ho α
C2
C1
A2
A1
B2
B1
П2
П1
О
Х
Х1
П4
П1
О1
C4
A4
B4
1.Через прямую AВ проводим пл. α П1(след
hoα сoвnадает с горизонтальной проекцией прямой А1В1). (α ┴П1,)
∩ ( A1В1 h0α).
∩
Слайд 89
ho α
C2
C1
A2
A1
B2
B1
П2
П1
О
Х
Х1
П4
П1
О1
C4
A4
B1
K4
L4
L4
K4
K2
L2
R
R
Любая плоскость пересекающая поверхность сферы, пересекает, по
окружности, проекции которой при донном расположении прямой проецируются на
пл. П2 в виде эллипса. Чтобы избежать построения эллипса. применим метод перемены пл. проекций, заменив пл. Пг пл.П4 // А1 В1 Тогда ось О1,Х1 будет // А1В1
2. Проецируем на пл. П4 заданную прямую AВ и cфepy. Тогда сечение сферы пл. α на пл. П4 изобразится в виде окружности радиуса R. 3. В пересечении полученного сечения с пряной AВ и определятся искомые точки KuL (К4,L4) которые обратным проецированием определяем в заданной системе,
Слайд 90
ho α
C2
C1
A2
A1
B2
B1
П2
П1
О
Х
Х1
П4
П1
О1
C4
A4
B1
K4
L4
L1
K1
K2
L2
3. Определяем видимость прямой
назад
назад
далее
Слайд 91
Точка на комплексном чертеже
ЗАДАЧИ
Слайд 92
Задача По заданным координатам точек А; В; С;
D; E; F;G; К построить их горизонтальные, фронтальные и
профильные проекции. Определить, в каких октантах расположены точки;
назад
назад
далее
Слайд 93
Задача Построить проекции отрезка прямой А В по
заданным координатам его концов. Найти следы прямой.
назад
назад
далее
Слайд 94
Задача . Определить натуральную длину отрезка прямой АВ
и углы наклона этой прямой к плоскостям проекций π1
и π2
x
A2
A1
B2
B1
z
0
y
назад
назад
далее
Слайд 95
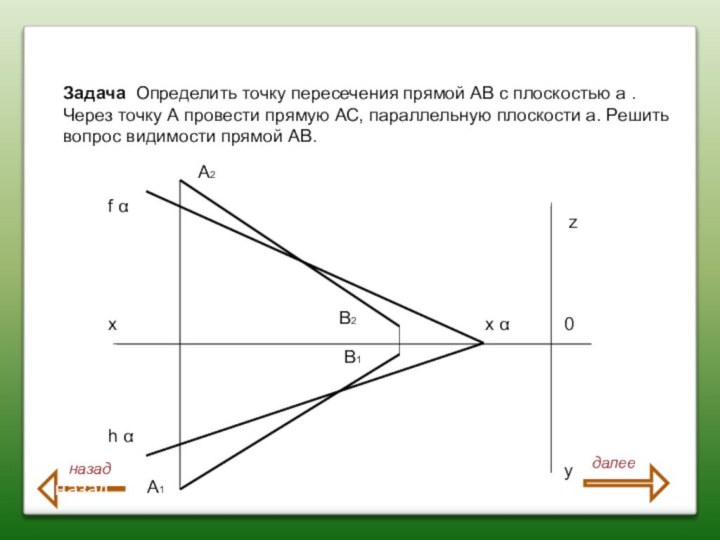
Задача Определить точку пересечения прямой АВ с плоскостью
а . Через точку А провести прямую АС, параллельную
плоскости а. Решить вопрос видимости прямой АВ.
f α
h α
A1
А2
B2
B1
x α
z
0
y
x
назад
назад
далее
Слайд 96
Задача Построить следы плоскости а, заданной тремя точками
А,В,С.В плоскости а построить горизонталь, отстоящую на расстоянии двух
единиц от горизонтальной плоскости π1 и фронталь отстоящую на расстоянии трех единиц от фронтальной плоскости проекций π2.
A2
A1
B1
B2
C1
C2
z
0
y
x
назад
назад
далее
Слайд 97
Задача По заданным координатам вершин построить проекции треугольников
ABC и DEF. Определить линию их пересечения. Решить вопрос
видимости объектов.
назад
назад
далее