Презентация на тему к проекту Теорема Вариньона и ее практическое применение

ПАРАЛЛЕЛОГРАММ ВАРИНЬОНА, БИМЕДИАНЫ ЧЕТЫРЕХУГОЛЬНИКА, ТЕОРЕМА ВАРИНЬОНА И СЛЕДСТВИЯ ИЗ

НЕЁ

ПРОБЛЕМЫ – ВЫЯСНИТЬ, ДЕЙСТВИТЕЛЬНО ЛИ ПАРАЛЛЕЛОГРАММ ВАРИНЬОНА ПОЗВОЛЯЕТ РАЦИОНАЛЬНЕЙ ПОЛУЧИТЬ РЕШЕНИЕ ЗАДАЧИ

ГИПОТЕЗА ИССЛЕДОВАНИЯ – ПАРАЛЛЕЛОГРАММ ВАРИНЬОНА НАДЕЖНЫЙ ПОМОЩНИК В РЕШЕНИИ ЗАДАЧ

применять ее с наименьшими временными затратами
ЗАДАЧИ:
А)Изучить теоретический материал: параллелограмм

Вариньона, бимедианы четырехугольника , теорему Вариньона и следствия из нее.
Б)Сравнить количество времени, необходимое для решения задач традиционным способом и с помощью теоремы Вариньона.
В)Выяснить практическое применение данной теоремы в задачах по геометрии школьного курса и в конкурсных задачах.

сторон

член Парижской Академии наук, профессор математики колледжа Мазарини. Ему

принадлежит одна из основных теорем о бимедианах четырехугольника.
Вариньон написал учебник по элементарной геометрии, в котором эта теорема впервые появилась.

выпуклого четырехугольника, является параллелограммом, и его площадь равна половине

площади данного четырехугольника

Выпуклый четырехугольник

Самопересекающийся четырехугольник

Вогнутый четырехугольник

1)KLMN-параллелограмм;

2)SKLMN=SABCD/2
Доказательство
1. Рассмотрим одну из сторон четырехугольника KLMN , например KL . Так как KL - средняя линия  ABC , то KL ║AC . По тем причинам MN ║AC . → KL ║NM и KL= MN= AC/2 . →  KLMN  - параллелограмм. Этот параллелограмм называется параллелограммом Вариньона данного четырехугольника ABCD.
2. Средняя линия отсекает от него , S которого в 4 раза < S исходного . Поэтому сама ∑ S 1-ого и 3-го треугольников равна ¼ S всего четырехугольника. То же и относительно ∑ S 2-го и 4-го треугольников. Поэтому S KLMN составляет ½ S ABCD
Теорема доказана.

лежит на середине отрезка, соединяющего середины сторон исходного четырёхугольника

(в этой же точке пересекаются отрезки, соединяющие середины противоположных сторон — диагонали вариньоновского параллелограмма).

2. Периметр параллелограмма Вариньона равен сумме диагоналей исходного четырёхугольника.

3. Площадь параллелограмма Вариньона равна половине площади исходного четырёхугольника.

4. Для прямоугольника и равнобедренной трапеции параллелограммом Вариньона является ромб, а для ромба — прямоугольник.

треугольника. Получаем:



Формулировка: Суммы площадей накрест лежащих четырехугольников, образованных пересечением

бимедиан  LN и KM выпуклого четырехугольника ABCD  равны.

четырехугольника и теорему Вариньона, которые встречаются в школьном курсе

геометрии (№567, 568)
Задача 1.
Докажите, что а) середины сторон прямоугольника являются вершинами ромба. И наоборот, б) середины сторон ромба являются вершинами прямоугольника.
Доказательство.
а) Диагонали прямоугольника равны, поэтому середины сторон прямоугольника являются вершинами ромба;
Стороны прямоугольника перпендикулярны, поэтому бимедианы перпендикулярны, тогда середины сторон прямоугольника являются вершинами ромба.
б) диагонали ромба перпендикулярны, поэтому середины сторон ромба являются вершинами прямоугольника;
Стороны ромба равны, поэтому середины сторон ромба являются вершинами прямоугольника.

на 2n равных частей, а затем точки деления на

противоположных сторонах соединены так, чтобы получилась «косоугольная шахматная доска», состоящая из белых и черных «клеток» (n = 2). Доказать, что сумма площадей всех белых «клеток» равна сумме площадей всех черных «клеток».

ДОКАЗАТЕЛЬСТВО
Из следствия следует, что точки пересечения отрезков на этой доске делят каждый на равные части.
Тогда в любом «маленьком» четырехугольнике, куда входят ровно две белые и две черные клетки, выполняются условия теоремы о бабочках.
Нужное равенство установлено.

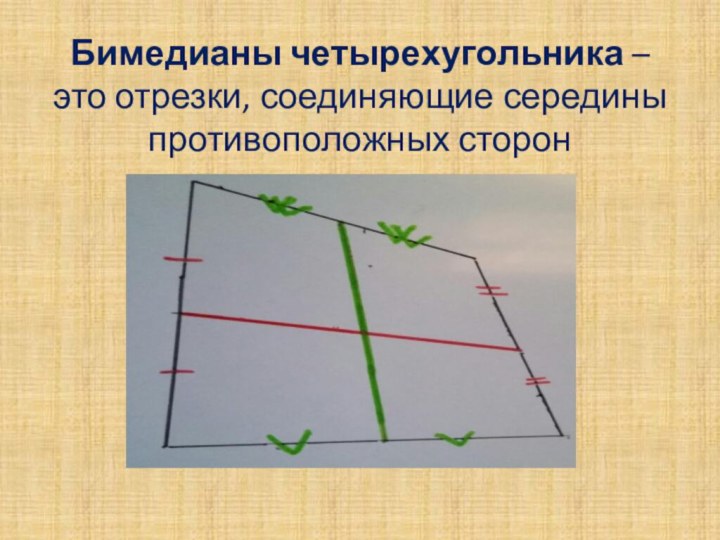
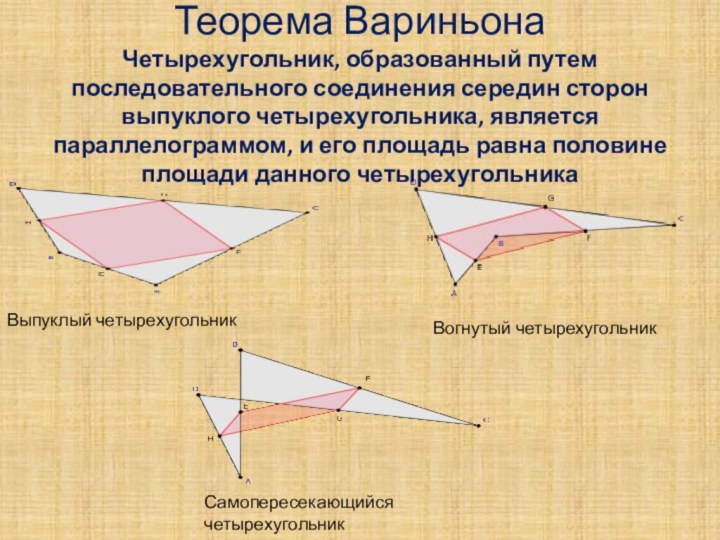
её использования.

Докажите, что середины сторон прямоугольника являются вершинами ромба.

И наоборот.

1-ый способ 1- AC – диагональ. FM - средняя линия треугольника ABC. NK – средняя линия треугольника ADC. Треугольники ABC и ADC равны по третьему признаку равенства треугольников (AB=DC, BC=AD, AC – общая сторона) => KN=FM. Также KN||FM (AC||FM, AC||KN) => KFMN- параллелограмм. 2- из первого следует, что KN=FM. Аналогично можно доказать, что FK=MN.  3- ABCD – прямоугольник => AC=BD. => KF=FM=MN=NK=> KFMN – ромб. 

2-ой способ  А) Диагонали прямоугольника равны, поэтому середины сторон прямоугольника являются вершинами ромба (из следствия теоремы Вариньона); Б) Стороны прямоугольника перпендикулярны, поэтому бимедианы перпендикулярны, тогда середины сторон прямоугольника являются вершинами ромба (из следствия теоремы Вариньона).

старое, чего мы не знаем», – сказал американский литератор

Лоренс Питер.

Пьер Вариньон жил в 18 веке, но теорема Вариньона как нельзя актуальна именно в наши дни, когда, чтобы всё успеть, необходимо гораздо больше, чем 24 часа в сутки.
Поэтому была поставлена цель: изучить теорему Вариньона и научиться применять ее на практике с наименьшими временными затратами.
Теорема Вариньона – красивейшая опорная задача, которая помогает решить, что называется, в один присест, массу планиметрических задач, в том числе повышенной сложности и олимпиадных.

четырехугольника // Математика . 2006 - №22.
2. Прасолов В.В.

Задачи по планиметрии. – Т.1,2 –М.: Наука, 1995
3. Штейнгауз Г. Математический калейдоскоп. - М.:Наука, 1981
4. BestReferat.ru// Бимедианы четырехугольника
5. dic.academic.ru// Что такое теорема о бабочках?
6. infourok.ru> issledovatelskaya… teorema variona // Исследовательская работа «Теорема Вариньона»
7. peoplе.su // Пьер Вариньон биография
8. referat.yabotanik.ru// бимедианы четырехугольника/ реферат по математике.
9. ru.vikipedia/org> Теорема Вариньона (геометрия)
10. treugolniki.ru>teorema-varinjоna// Лекции и примеры решения задач