Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

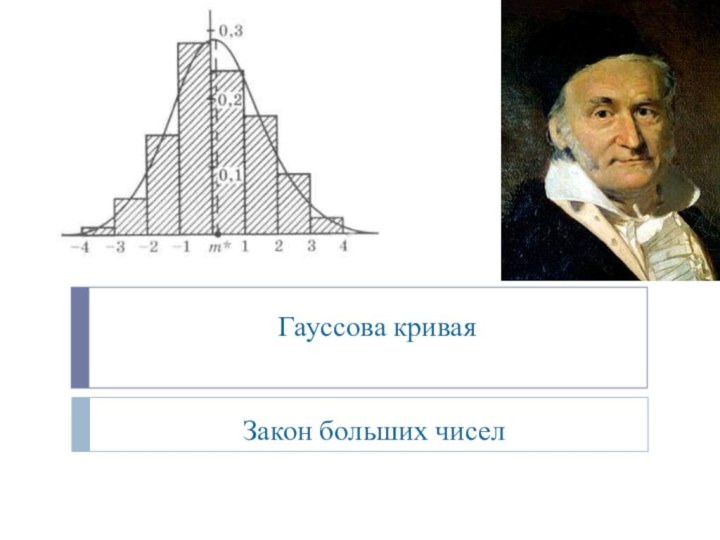
Презентация на тему к уроку на тему: Гауссова кривая (11 класс)

Содержание

2. Карл Фридрих ГауссРодился: 30 апреля 1777 года в городе
4. График функции y = (x) называют гауссовой кривой
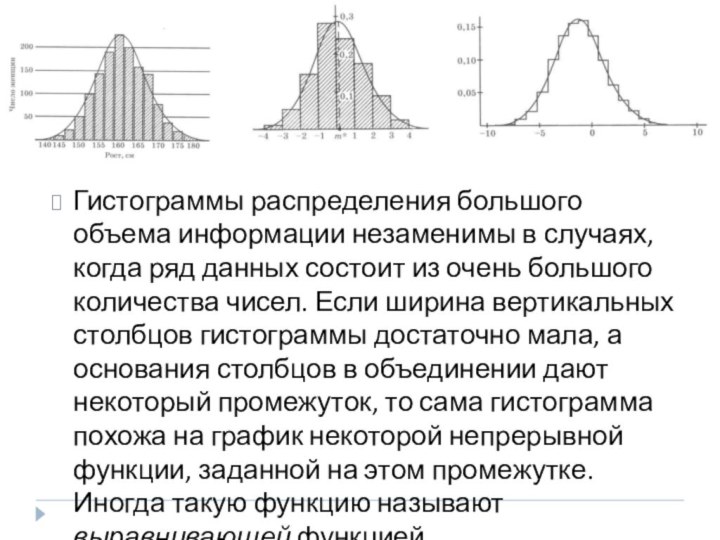
5. Гистограммы распределения большого объема информации незаменимы в
6. Рост женщин по выборке из 1375 женщин
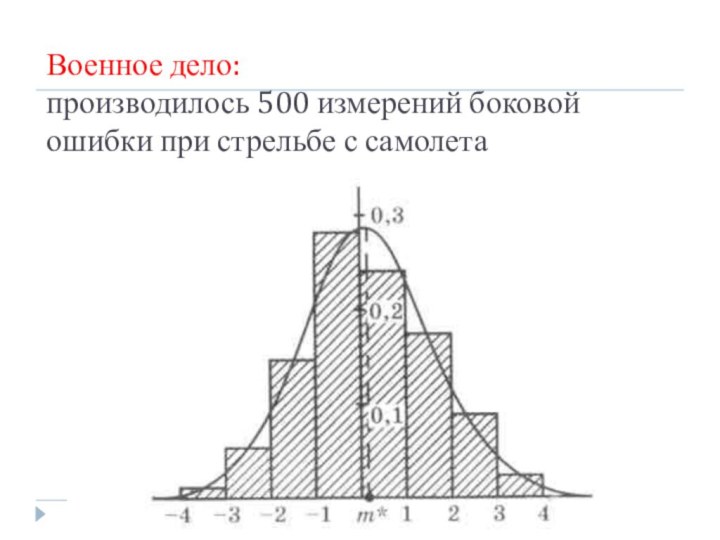
7. Военное дело: производилось 500 измерений боковой ошибки при стрельбе с самолета
8. Биология. Измерение размера 12000 бобов (изучались величины отклонений от среднего размера
9. Графики функций выравнивающих гистограммы похожи
10. Доска ГальтонаДля наглядной демонстрации действии гауссова закона распределения иногда используют специальное устройство — доску Гальтона
11. Существует способ приближенных вычислений вероятности Pn(k) наступления
12. Алгоритм использования функции у =
13. Вероятности Pn(k), как правило, весьма
15. График функции y=Ф(х)
16. Алгоритм использования функции у = Ф(х) в
17. Скачать презентацию
18. Похожие презентации

Карл Фридрих ГауссРодился: 30 апреля 1777 года в городе БрауншвейгУмер: 23 февраля 1855 в возрасте 77 лет.В алгебре открыл кольцо целых комплексных гауссовых чисел, создал для них теорию делимости и с их помощью решил немало алгебраических проблем. Указал знакомую теперь всем геометрическую модель комплексных чисел и действий

Главная
Разное
Презентация к уроку на тему: Гауссова кривая (11 класс)

Карл Фридрих ГауссРодился: 30 апреля 1777 года в городе БрауншвейгУмер: 23 февраля 1855 в возрасте 77 лет.В

Презентация к уроку на тему: Гауссова кривая (11 класс)

График функции y = (x) называют гауссовой кривой

Гистограммы распределения большого объема информации незаменимы в случаях, когда ряд данных состоит

Военное дело: производилось 500 измерений боковой ошибки при стрельбе с самолета

Биология. Измерение размера 12000 бобов (изучались величины отклонений от среднего размера

Графики функций выравнивающих гистограммы похожи друг на друга. Все эти

Доска ГальтонаДля наглядной демонстрации действии гауссова закона распределения иногда используют специальное устройство — доску Гальтона

Существует способ приближенных вычислений вероятности Pn(k) наступления k «успехов» в n независимых

Алгоритм использования функции у = (х) в приближенных вычисленияхпроверить

Вероятности Pn(k), как правило, весьма малы. Поэтому при

Алгоритм использования функции у = Ф(х) в приближенных вычислениях проверить справедливость неравенства

Закон больших чисел Для каждого положительного числа r при неограниченном увеличении

Слайды презентации

Слайд 2 Карл Фридрих Гаусс
Родился: 30 апреля 1777 года в городе Брауншвейг
Умер:

Карл Фридрих ГауссРодился: 30 апреля 1777 года в городе БрауншвейгУмер: 23 февраля 1855 в возрасте 77

23 февраля 1855 в возрасте 77 лет.

В алгебре открыл кольцо целых комплексных гауссовых чисел,

создал для них теорию делимости и с их помощью решил немало алгебраических проблем. Указал знакомую теперь всем геометрическую модель комплексных чисел и действий с ними.

Слайд 3

Слайд 4 График функции y = (x) называют

гауссовой кривой

Слайд 5 Гистограммы распределения большого объема информации незаменимы в случаях,

Гистограммы распределения большого объема информации незаменимы в случаях, когда ряд данных

когда ряд данных состоит из очень большого количества чисел.

Если ширина вертикальных столбцов гистограммы достаточно мала, а основания столбцов в объединении дают некоторый промежуток, то сама гистограмма похожа на график некоторой непрерывной функции, заданной на этом промежутке. Иногда такую функцию называют выравнивающей функцией.

Слайд 6 Рост женщин по выборке из 1375 женщин

Слайд 7 Военное дело: производилось 500 измерений боковой ошибки при

стрельбе с самолета

Слайд 8 Биология. Измерение размера 12000 бобов (изучались величины отклонений от

среднего размера

Слайд 9
Графики функций выравнивающих гистограммы похожи друг

на друга. Все эти кривые распределения получаются из гауссовой

кривой. Ее часто называют кривой нормального распределения.

Слайд 10 Доска Гальтона

Для наглядной демонстрации действии гауссова закона распределения

иногда используют специальное устройство — доску Гальтона

Слайд 11 Существует способ приближенных вычислений вероятности Pn(k) наступления k

Существует способ приближенных вычислений вероятности Pn(k) наступления k «успехов» в n

«успехов» в n независимых повторениях эксперимента с помощью гауссовой

функции.
Для гауссовой функции имеются подробные таблицы ее значений. Эти таблицы составлены для значений аргумента х с шагом 0,01.

Слайд 12 Алгоритм использования функции у = (х)

Алгоритм использования функции у = (х) в приближенных вычисленияхпроверить справедливость

в приближенных вычислениях
проверить справедливость неравенства npq >10;

вычислить xk по

формуле xk = ;

по таблице значений гауссовой функции вычислить ϕ(xk);
предыдущий результат разделить на

Слайд 13 Вероятности Pn(k), как правило, весьма малы.

Вероятности Pn(k), как правило, весьма малы. Поэтому при большом

Поэтому при большом числе n в схеме

Бернулли для числа k «успехов» устанавливают не одно точное значение, а некоторые рамки, в пределах которых разрешено меняться числу k.
Вероятность того, что число «успехов» k в n испытаниях Бернулли находится в пределах от k1 до k2, обозначают так: Pn(k1 ≤ k ≤ k2).