Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Деление окружности сопряжения

Содержание

2. Содержание: Что такое сопряжение.Основные элементы сопряжения и их виды.Как разделить окружность на равные части.Сопряжение пересекающихся прямых дугой окружности определенного радиуса.
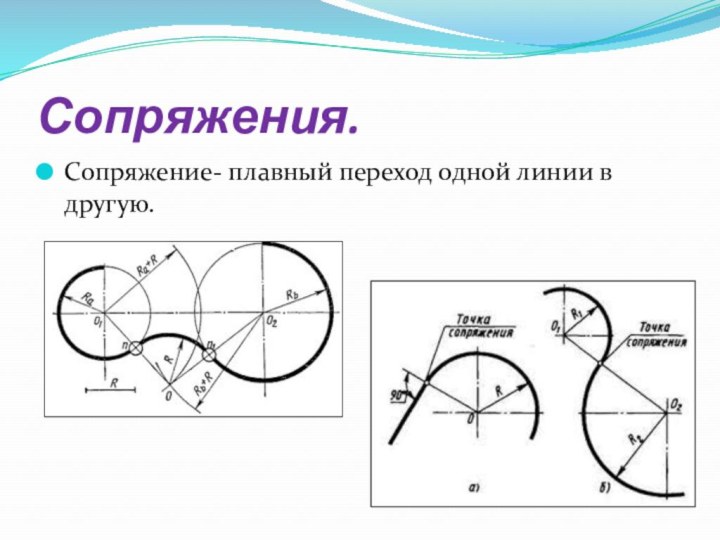
3. Сопряжения.Сопряжение- плавный переход одной линии в другую.
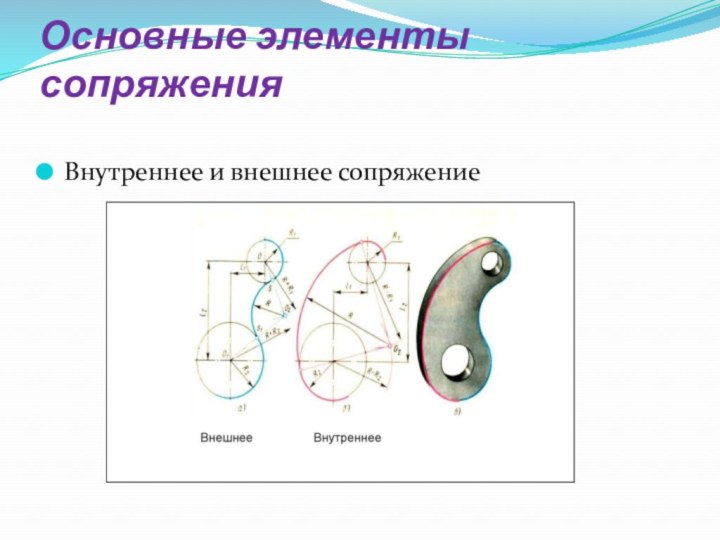
4. Основные элементы сопряженияВнутреннее и внешнее сопряжение
5. Сопряжение двух сторон прямого, острого и тупого углов с дугой.
6. Непосредственные сопряжения.-сопряжения, в которых одна линия плавно переходит в другую без промежуточных линий.
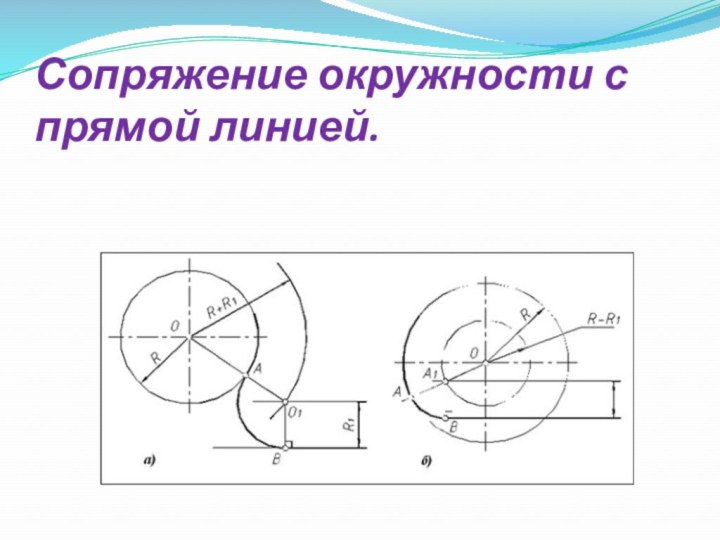
7. Сопряжение окружности с прямой линией.
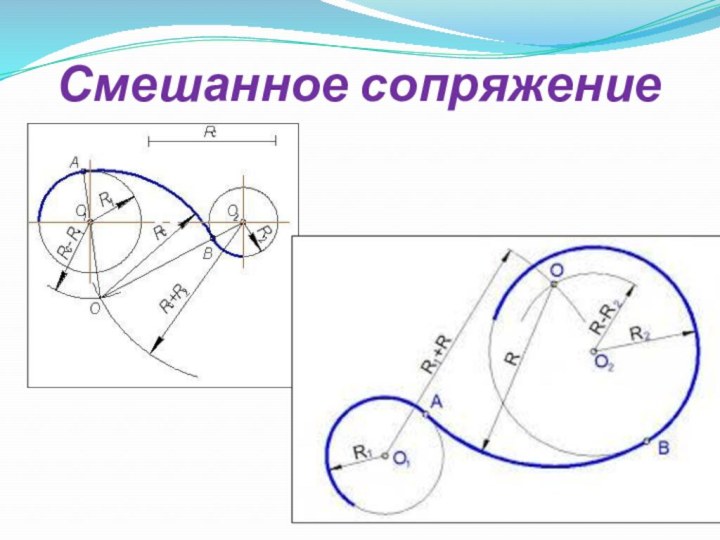
9. Смешанное сопряжение
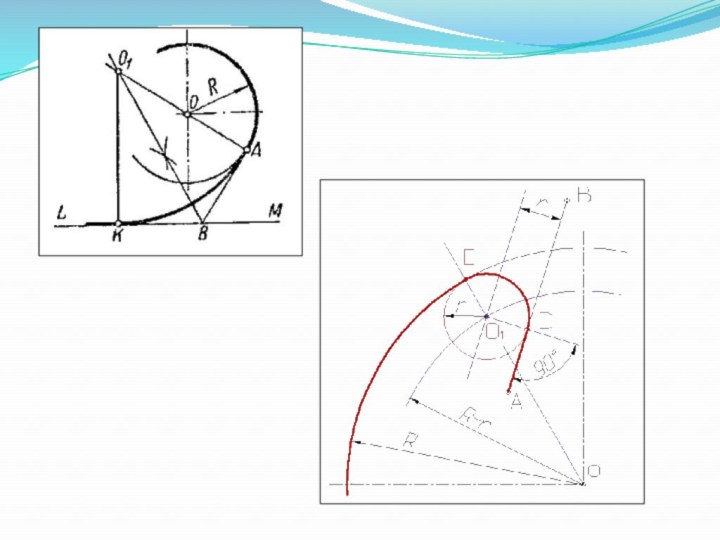
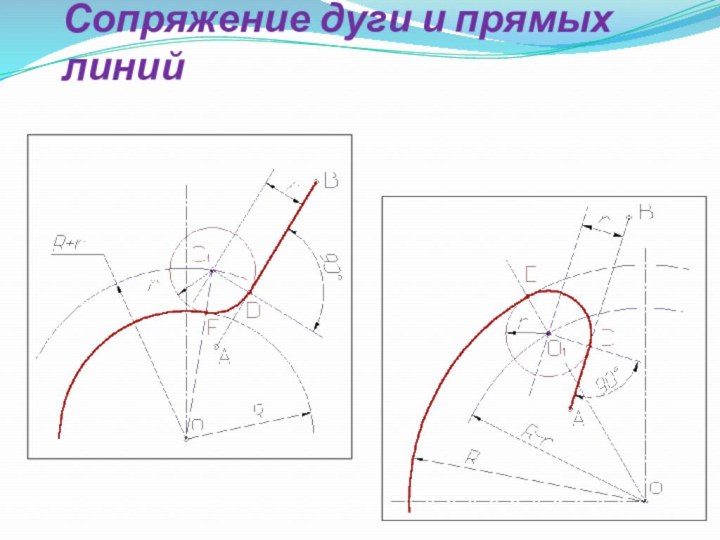
10. Сопряжение дуги и прямых линий
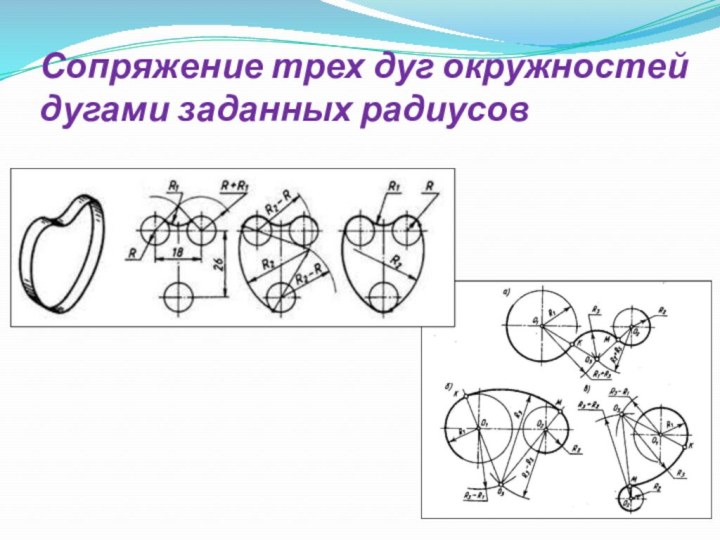
11. Сопряжение трех дуг окружностей дугами заданных радиусов
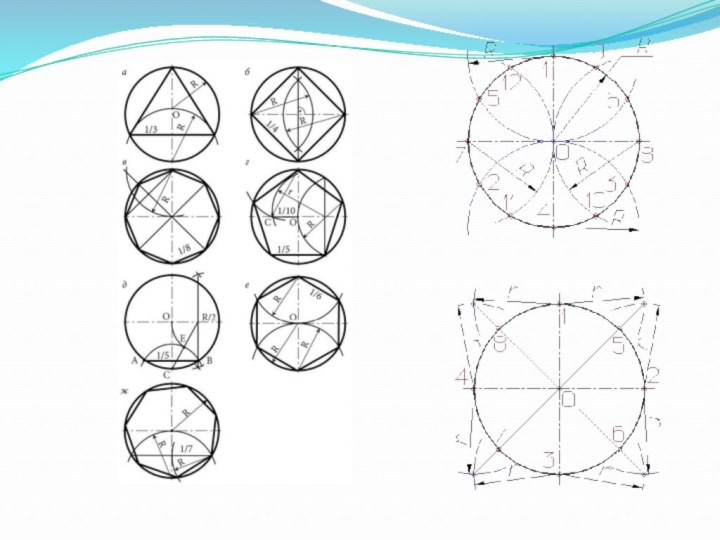
12. Деление окружности на равные частиВ основе построения
14. Деление окружности на две, четыре и
15. Деление окружности на восемь равных частей можно выполнять при помощи циркуля или при помощи линейки и угольника с углами. Прием 1:«Деление окружности на восемь равных частей с помощью циркуля». Из точек 1 и 7 провести две дуги произвольного радиуса.Через полученную точку пересечения этих дуг и центр окружности провести диаметр провести диаметр 4‐8.Таким же образом построить второй диаметр 2‐6 (рис. 1а).
16. Прием 2: «Деление окружности на восемь равных частей с помощью угольника с углами и линейки»:Провести две взаимно перпендикулярные вертикальную и горизонтальную штрихпунктирные линии, тем самым окружность будет поделена на 4 части.Переместить линейку параллельно горизонтальной штрихпунктирной линии вниз, поставить над линейкой угольник так, чтобы гипотенуза проходила через центр окружности и получить диаметр 2‐6.Перевернуть угольник и построить второй диаметр 8-4 (рис. 1б)
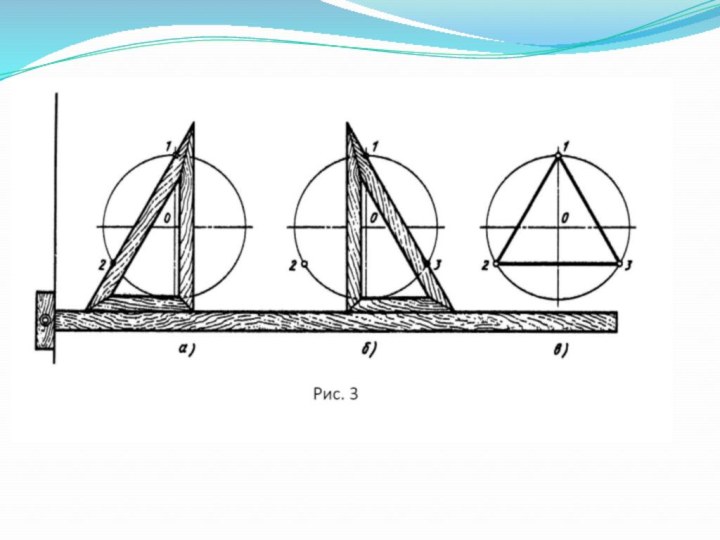
17. Деление окружности на три равные части и построение правильного вписанного треугольника можно выполнить с помощью циркуля или угольника с углами 30, 60 и 90
19. Прием 2«Деление окружности на равные части при помощи линейки и угольника с углами 30, 60 и 90°»: Провести две взаимно перпендикулярные вертикальную и горизонтальную штрихпунктирные линии.Переместить линейку горизонтально штрихпунктирной линии вниз, поставить над линейкой угольник так, чтобы сторона с углом 60° угольника касалась линейки (см. рис.3). Провести линии через точку 1 до пересечения с окружностью в точках 2 и 3(рис.3 а и б).Точки 2 и 3 соединить и получить правильный вписанный треугольник (рис.3 в).
21. Деление окружности на шесть равных частей и построение правильного вписанного шестиугольника можно выполнить при помощи циркуля или угольника с углами 30,60 и 90 ° и линейки.
23. Прием 2 Первый случай:Провести две взаимно перпендикулярные
25. Второй случай:Провести две взаимно перпендикулярные вертикальную и
26. Деление окружности на двенадцать равных частей и построение правильного вписанного двенадцатиугольника можно выполнить при помощи циркуля или угольника с углами 30,60 и 90 ° и линейки. Прием 1:«Деление окружности на двенадцать равных частей при помощи циркуля» Провести две взаимно перпендикулярные вертикальную и горизонтальную штрихпунктирные линии. Из четырех концов двух взаимно перпендикулярных штрихпунктирных линий окружности провести дуги, равные радиусу данной окружности, до пересечения с окружностью. Последовательно соединить полученные точки и получить правильный вписанный двенадцатиугольник.
28. Прием 2:«Деление окружности на двенадцать равных частей при помощи линейки и угольника с углами 30,60 и 90 °»Провести две взаимно перпендикулярные вертикальную и горизонтальную штрихпунктирные линии.Переместить линейку параллельно горизонтальной штрихпунктирной линии вниз, поставить над линейкой угольник так, чтобы угол 60° угольника касалась линейки . ( рис.5)Провести линии через точки пересечения горизонтальной штрихпунктирной линии с окружностью до пересечения с окружностью. Поставить над линейкой угольник так, чтобы угол 30° угольника касалась линейки (рис.6)Провести линии через точки пересечения вертикальной штрихпунктирной линии с окружностью до пересечения с окружностью.Последовательно соединить полученные точки и получить правильный вписанный двенадцатиугольник.
30. Сопряжение пересекающихся прямых дугой окружности данного радиуса Провести две линии центров параллельно каждой на расстоянии, равном радиусу R дуги сопряжения (рис.10). Точка их пересечения будет центром дуги сопряжения.Из центра сопряжения O провести перпендикуляры на заданные прямые и получить точки сопряжения К и К1.Из точки О радиусом R провести дугу сопряжения.
31. Сопряжение окружности и прямой линии дугой заданного радиуса R.Из центра O данной окружности радиуса R провести дугу вспомогательной окружности радиуса R+R1.Провести прямую, параллельную заданной, на расстоянии R1. Точка пересечения проведенной прямой и дуги вспомогательной окружности будет центром дуги сопряжения O1 .Соединить найденный центр O1 и центр окружности О и получить точку сопряжения К.Опустить перпендикуляр с центра дуги окружности O1 на заданную прямую и получить точку сопряжения K1.Из точки O1 радиусом R1 провести дугу сопряжения.Внешнее касание:
33. Внутреннее касание.Из центра O данной окружности радиуса R провести дугу вспомогательной окружности радиуса R+R1.Провести прямую, параллельную заданной, на расстоянии R1. Точка пересечения проведенной прямой и дуги вспомогательной окружности будет центром дуги сопряжения O1 .Соединить найденный центр O1 и центр окружности О и получить точку сопряжения К.Опустить перпендикуляр с центра дуги окружности O1 на заданную прямую и получить точку сопряжения K1.Из точки O1 радиусом R1 провести дугу сопряжения.
35. Сопряжение двух окружностей дугой заданного
37. Из центра O1 данной окружности радиуса R1
39. Из центра O1 данной окружности радиуса R1
41. Скачать презентацию
42. Похожие презентации

Содержание: Что такое сопряжение.Основные элементы сопряжения и их виды.Как разделить окружность на равные части.Сопряжение пересекающихся прямых дугой окружности определенного радиуса.

Главная
Разное
Презентация Деление окружности сопряжения

МБОУ СОШ №68Тема:»Деление окружности сопряжения»Подготовила: Керницкая Ю.В.

Содержание: Что такое сопряжение.Основные элементы сопряжения и их виды.Как разделить окружность на равные части.Сопряжение пересекающихся прямых дугой окружности определенного радиуса.

Сопряжения.Сопряжение- плавный переход одной линии в другую.

Основные элементы сопряженияВнутреннее и внешнее сопряжение

Сопряжение двух сторон прямого, острого и тупого углов с дугой.

Непосредственные сопряжения.-сопряжения, в которых одна линия плавно переходит в другую без промежуточных линий.

Презентация Деление окружности сопряжения

Сопряжение трех дуг окружностей дугами заданных радиусов

Деление окружности на равные частиВ основе построения правильных различных многоугольников лежит деление

Деление окружности на две, четыре и восемь частей Существует два способа деления окружности на равные части и построение правильных вписанных многоугольников: с помощью циркуля или с помощью угольников и линейки (рекомендуется взять линейку на роликах, т.е рейсшину). Деление окружности на две и четыре равные части

Деление окружности на восемь равных частей можно выполнять при помощи циркуля или при помощи линейки и угольника с углами. Прием 1:«Деление окружности на восемь равных частей с помощью циркуля». Из точек 1 и 7 провести две дуги произвольного радиуса.Через полученную точку пересечения этих дуг и центр окружности провести диаметр провести диаметр 4‐8.Таким же образом построить второй диаметр 2‐6 (рис. 1а).

Прием 2: «Деление окружности на восемь равных частей с помощью угольника с углами и линейки»:Провести две взаимно перпендикулярные вертикальную и горизонтальную штрихпунктирные линии, тем самым окружность будет поделена на 4 части.Переместить линейку параллельно горизонтальной штрихпунктирной линии вниз, поставить над линейкой угольник так, чтобы гипотенуза проходила через центр окружности и получить диаметр 2‐6.Перевернуть угольник и построить второй диаметр 8-4 (рис. 1б)

Деление окружности на три равные части и построение правильного вписанного треугольника можно выполнить с помощью циркуля или угольника с углами 30, 60 и 90 и линейки.Деление окружности на три,

Прием 2«Деление окружности на равные части при помощи линейки и угольника с углами 30, 60 и 90°»: Провести две взаимно перпендикулярные вертикальную и горизонтальную штрихпунктирные линии.Переместить линейку горизонтально штрихпунктирной линии вниз, поставить над линейкой угольник так, чтобы сторона с углом 60° угольника касалась линейки (см. рис.3). Провести линии через точку 1 до пересечения с окружностью в точках 2 и 3(рис.3 а и б).Точки 2 и 3 соединить и получить правильный вписанный треугольник (рис.3 в).

Деление окружности на шесть равных частей и построение правильного вписанного шестиугольника можно выполнить при помощи циркуля или угольника с углами 30,60 и 90 ° и линейки.

Прием 2 Первый случай:Провести две взаимно перпендикулярные вертикальную и горизонтальную штрихпунктирные линии.Переместить

Второй случай:Провести две взаимно перпендикулярные вертикальную и горизонтальную штрихпунктирные линии.Переместить линейку параллельно

Деление окружности на двенадцать равных частей и построение правильного вписанного двенадцатиугольника можно выполнить при помощи циркуля или угольника с углами 30,60 и 90 ° и линейки. Прием 1:«Деление окружности на двенадцать равных частей при помощи циркуля» Провести две взаимно перпендикулярные вертикальную и горизонтальную штрихпунктирные линии. Из четырех концов двух взаимно перпендикулярных штрихпунктирных линий окружности провести дуги, равные радиусу данной окружности, до пересечения с окружностью. Последовательно соединить полученные точки и получить правильный вписанный двенадцатиугольник.

Прием 2:«Деление окружности на двенадцать равных частей при помощи линейки и угольника с углами 30,60 и 90 °»Провести две взаимно перпендикулярные вертикальную и горизонтальную штрихпунктирные линии.Переместить линейку параллельно горизонтальной штрихпунктирной линии вниз, поставить над линейкой угольник так, чтобы угол 60° угольника касалась линейки . ( рис.5)Провести линии через точки пересечения горизонтальной штрихпунктирной линии с окружностью до пересечения с окружностью. Поставить над линейкой угольник так, чтобы угол 30° угольника касалась линейки (рис.6)Провести линии через точки пересечения вертикальной штрихпунктирной линии с окружностью до пересечения с окружностью.Последовательно соединить полученные точки и получить правильный вписанный двенадцатиугольник.

Сопряжение пересекающихся прямых дугой окружности данного радиуса Провести две линии центров параллельно каждой на расстоянии, равном радиусу R дуги сопряжения (рис.10). Точка их пересечения будет центром дуги сопряжения.Из центра сопряжения O провести перпендикуляры на заданные прямые и получить точки сопряжения К и К1.Из точки О радиусом R провести дугу сопряжения.

Сопряжение окружности и прямой линии дугой заданного радиуса R.Из центра O данной окружности радиуса R провести дугу вспомогательной окружности радиуса R+R1.Провести прямую, параллельную заданной, на расстоянии R1. Точка пересечения проведенной прямой и дуги вспомогательной окружности будет центром дуги сопряжения O1 .Соединить найденный центр O1 и центр окружности О и получить точку сопряжения К.Опустить перпендикуляр с центра дуги окружности O1 на заданную прямую и получить точку сопряжения K1.Из точки O1 радиусом R1 провести дугу сопряжения.Внешнее касание:

Внутреннее касание.Из центра O данной окружности радиуса R провести дугу вспомогательной окружности радиуса R+R1.Провести прямую, параллельную заданной, на расстоянии R1. Точка пересечения проведенной прямой и дуги вспомогательной окружности будет центром дуги сопряжения O1 .Соединить найденный центр O1 и центр окружности О и получить точку сопряжения К.Опустить перпендикуляр с центра дуги окружности O1 на заданную прямую и получить точку сопряжения K1.Из точки O1 радиусом R1 провести дугу сопряжения.

Сопряжение двух окружностей дугой заданного радиуса R3.Внешнее касание:Из центра O1

Из центра O1 данной окружности радиуса R1 провести дугу вспомогательной окружности радиуса

Спасибо за внимание!Всех с наступающим Новым Годом!

Слайды презентации

Слайд 2 Содержание:
Что такое сопряжение.
Основные элементы сопряжения и их

виды.
Как разделить окружность на равные части.
Сопряжение пересекающихся прямых дугой окружности определенного радиуса.

Слайд 3 Сопряжения.
Сопряжение- плавный переход одной линии в другую.

Слайд 4 Основные элементы сопряжения
Внутреннее и внешнее сопряжение

Слайд 5 Сопряжение двух сторон прямого, острого и тупого углов

с дугой.

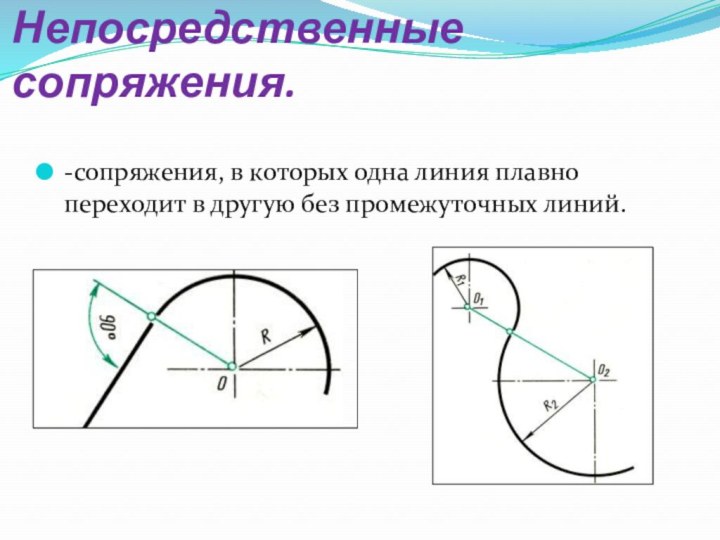
Слайд 6 Непосредственные сопряжения.
-сопряжения, в которых одна линия плавно переходит

в другую без промежуточных линий.

Слайд 7 Сопряжение окружности с прямой линией.

Слайд 9 Смешанное сопряжение

Слайд 10 Сопряжение дуги и прямых линий

Слайд 11 Сопряжение трех дуг окружностей дугами заданных радиусов

Слайд 12 Деление окружности на равные части
В основе построения правильных

различных многоугольников лежит деление описанной вокруг них окружности на

равные части

Слайд 14 Деление окружности на две, четыре и восемь

частей
Существует два способа деления окружности на равные части и построение правильных вписанных многоугольников: с помощью циркуля или с помощью угольников и линейки (рекомендуется взять линейку на роликах, т.е рейсшину). Деление окружности на две и четыре равные части можно выполнить, используя штрихпунктирные линии, изображающие центр окружности.

Эти штрихпунктирные линии делят окружность на равные части: вертикальная на две части (правую и левую), горизонтальная также на две части (верхнее и нижнее). В результате эта окружность разделена штрихпунктирными линиями на четыре равные части.(рис .1

а).

Слайд 15 Деление окружности на восемь равных частей можно выполнять при помощи циркуля или при помощи линейки и угольника с углами.
Прием 1:
«Деление окружности на восемь равных частей с помощью циркуля».
Из точек 1 и 7 провести две дуги произвольного радиуса.
Через полученную точку пересечения этих дуг и центр окружности провести диаметр провести диаметр 4‐8.
Таким же образом построить второй диаметр 2‐6 (рис. 1а).

Слайд 16 Прием 2: «Деление окружности на восемь равных частей с помощью угольника с углами и линейки»:
Провести две взаимно перпендикулярные вертикальную и горизонтальную штрихпунктирные линии, тем самым окружность будет поделена на 4 части.
Переместить линейку параллельно горизонтальной штрихпунктирной линии вниз, поставить над линейкой угольник так, чтобы гипотенуза проходила через центр окружности и получить диаметр 2‐6.
Перевернуть угольник и построить второй диаметр 8-4 (рис.

1б)

Слайд 17 Деление окружности на три равные части и построение правильного вписанного треугольника можно выполнить с помощью циркуля или угольника с углами 30, 60 и 90 и

линейки.

Деление окружности на три, шесть и двенадцать равных частей

Слайд 19 Прием 2
«Деление окружности на равные части при помощи линейки и угольника с углами 30, 60 и 90°»:
Провести две взаимно перпендикулярные вертикальную и горизонтальную штрихпунктирные линии.
Переместить линейку горизонтально штрихпунктирной линии вниз, поставить над линейкой угольник так, чтобы сторона с углом 60° угольника касалась линейки (см. рис.3).

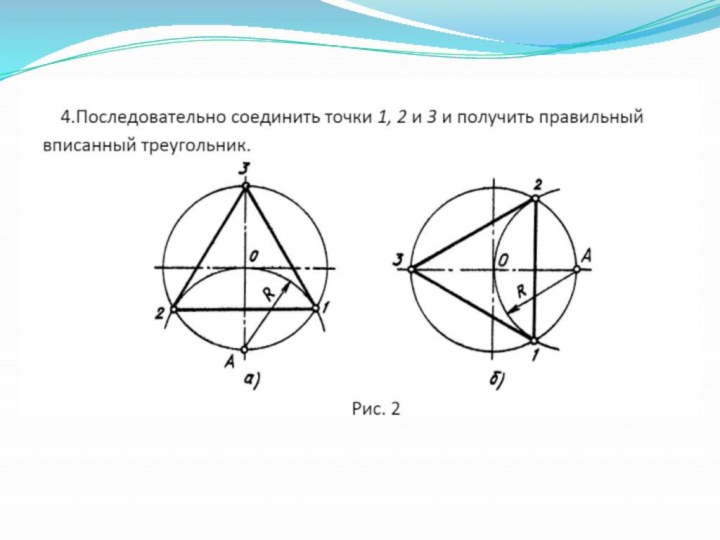
Провести линии через точку 1 до пересечения с окружностью в точках 2 и 3(рис.3 а и б).
Точки 2 и 3 соединить и получить правильный вписанный треугольник (рис.3 в).

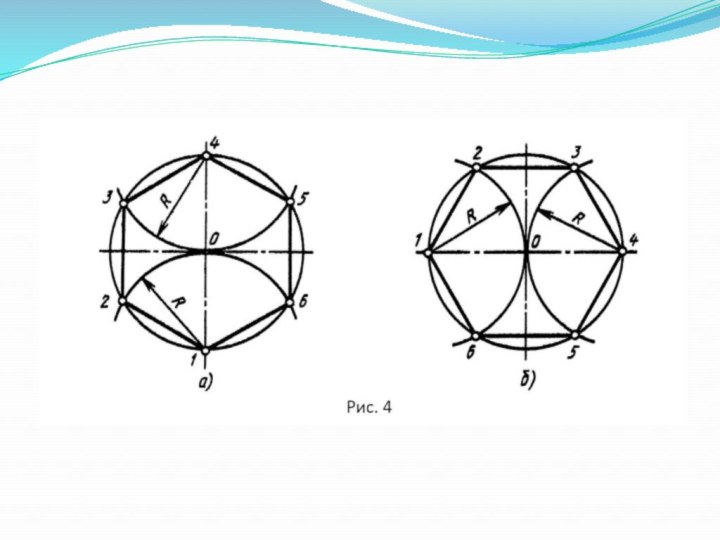
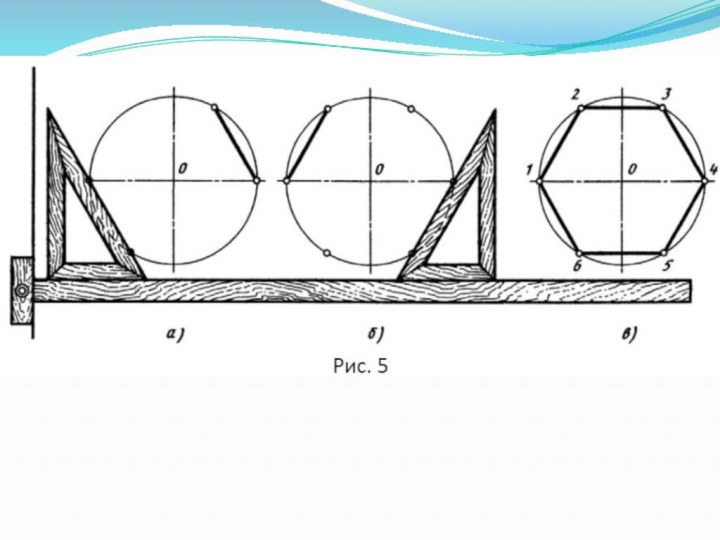
Слайд 21 Деление окружности на шесть равных частей и построение правильного вписанного шестиугольника можно выполнить при помощи циркуля или угольника с углами 30,60 и 90 ° и линейки.

Слайд 23 Прием 2
Первый случай:
Провести две взаимно перпендикулярные вертикальную

Прием 2 Первый случай:Провести две взаимно перпендикулярные вертикальную и горизонтальную штрихпунктирные

и горизонтальную штрихпунктирные линии.
Переместить линейку параллельно горизонтальной штрихпунктирной линии

вниз, поставить над линейкой угольник так, чтобы угол 60° угольника касался линейки (см. рис. 5)
Провести линии через точки пересечения горизонтальной штрихпунктирной линии с окружностью до пересечения с окружностью.
Соединить все полученные точки и получить правильный вписанный шестиугольник (рис. 5)

Слайд 24

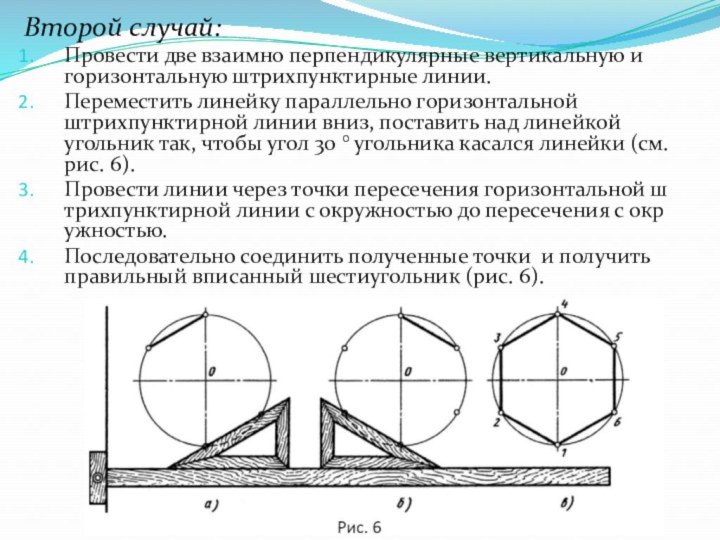
Слайд 25 Второй случай:
Провести две взаимно перпендикулярные вертикальную и горизонтальную

Второй случай:Провести две взаимно перпендикулярные вертикальную и горизонтальную штрихпунктирные линии.Переместить линейку

штрихпунктирные линии.
Переместить линейку параллельно горизонтальной штрихпунктирной линии вниз, поставить

над линейкой угольник так, чтобы угол 30 ° угольника касался линейки (см. рис. 6).
Провести линии через точки пересечения горизонтальной штрихпунктирной линии с окружностью до пересечения с окружностью.
Последовательно соединить полученные точки и получить правильный вписанный шестиугольник (рис. 6).

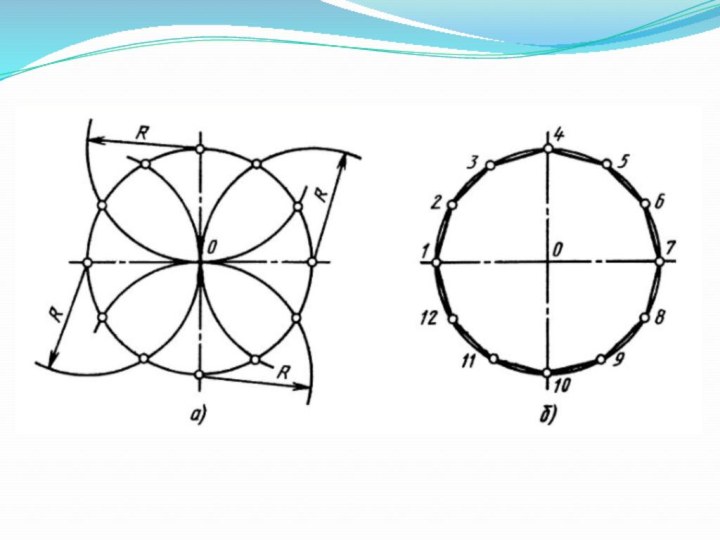
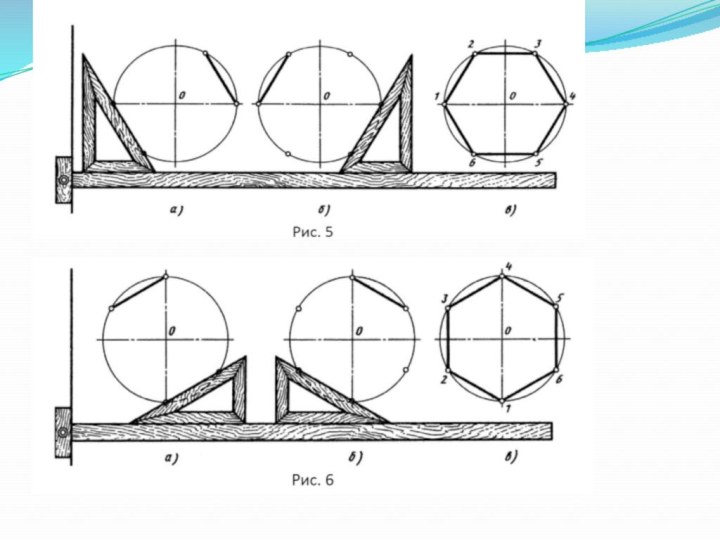
Слайд 26 Деление окружности на двенадцать равных частей и построение правильного вписанного двенадцатиугольника можно выполнить при помощи циркуля или угольника с углами 30,60 и 90 ° и линейки.
Прием 1:«Деление окружности на двенадцать равных частей при помощи циркуля»
Провести две взаимно перпендикулярные вертикальную и горизонтальную штрихпунктирные линии.

Из четырех концов двух взаимно перпендикулярных штрихпунктирных линий окружности провести дуги, равные радиусу данной окружности, до пересечения с окружностью.
Последовательно соединить полученные точки и получить правильный вписанный двенадцатиугольник.

Слайд 27

Слайд 28 Прием 2:«Деление окружности на двенадцать равных частей при помощи линейки и угольника с углами 30,60 и 90 °»

Провести две взаимно перпендикулярные вертикальную и горизонтальную штрихпунктирные линии.

Переместить линейку параллельно горизонтальной штрихпунктирной линии вниз, поставить над линейкой угольник так, чтобы угол 60° угольника касалась линейки . ( рис.5)

Провести линии через точки пересечения горизонтальной штрихпунктирной линии с окружностью до пересечения с окружностью.

Поставить над линейкой угольник так, чтобы угол 30° угольника касалась линейки (рис.6)
Провести линии через точки пересечения вертикальной штрихпунктирной линии с окружностью до пересечения с окружностью.
Последовательно соединить полученные точки и получить правильный вписанный двенадцатиугольник.

Слайд 29

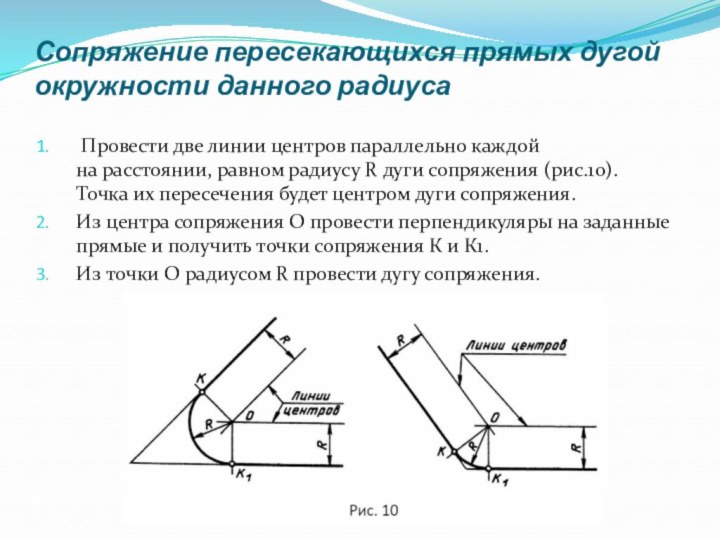
Слайд 30 Сопряжение пересекающихся прямых дугой окружности данного радиуса
Провести две линии центров параллельно каждой на расстоянии, равном радиусу R дуги сопряжения (рис.10). Точка их пересечения будет центром дуги сопряжения.
Из центра сопряжения O провести перпендикуляры на заданные прямые и получить

точки сопряжения К и К1.
Из точки О радиусом R провести дугу сопряжения.

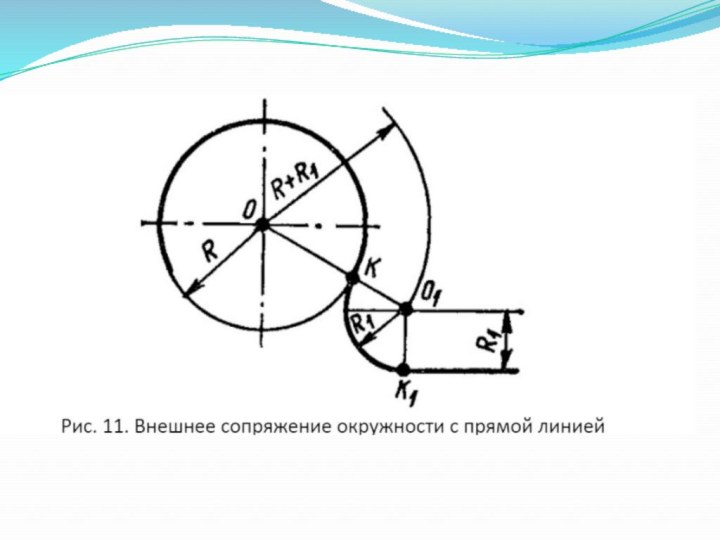
Слайд 31 Сопряжение окружности и прямой линии дугой заданного радиуса R.
Из центра O данной окружности радиуса R провести дугу вспомогательной окружности радиуса R+R1.
Провести прямую, параллельную заданной, на расстоянии R1. Точка пересечения проведенной прямой и

дуги вспомогательной окружности будет центром дуги сопряжения O1 .
Соединить найденный центр O1 и центр окружности О и получить точку сопряжения К.
Опустить перпендикуляр с центра дуги окружности O1 на заданную прямую и получить точку сопряжения K1.
Из точки O1 радиусом R1 провести дугу сопряжения.
Внешнее касание:

Слайд 32

Слайд 33 Внутреннее касание.
Из центра O данной окружности радиуса R провести дугу вспомогательной окружности радиуса R+R1.
Провести прямую, параллельную заданной, на расстоянии R1. Точка пересечения проведенной прямой и дуги вспомогательной окружности будет центром дуги сопряжения

O1 .
Соединить найденный центр O1 и центр окружности О и получить точку сопряжения К.
Опустить перпендикуляр с центра дуги окружности O1 на заданную прямую и получить точку сопряжения K1.
Из точки O1 радиусом R1 провести дугу сопряжения.

Слайд 34

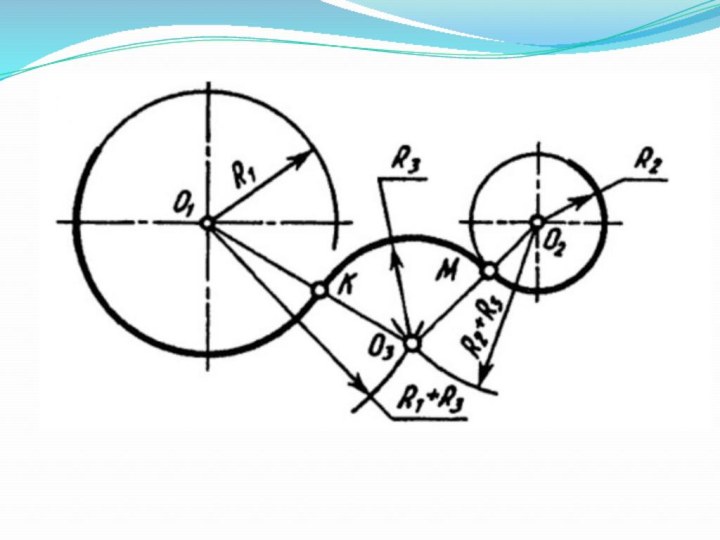
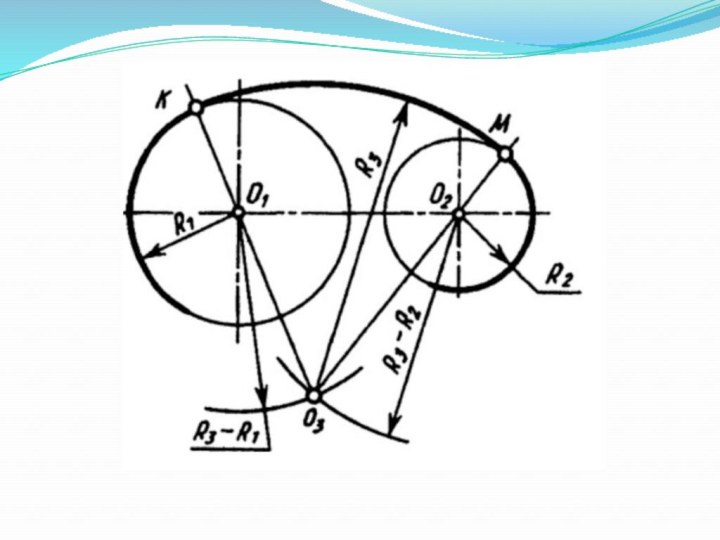
Слайд 35 Сопряжение двух окружностей дугой заданного радиуса

R3.
Внешнее касание:
Из центра O1 данной окружности радиуса R1 провести

дугу вспомогательной окружности радиуса R1+R2.
Из центра O2 данной окружности радиуса R2 провести дугу вспомогательной окружности радиуса R1+R2. Точка пересечения этих вспомогательных дуг окружности будет центром дуги сопряжения O2.
Соединить найденный центр О2 и центр окружности О1 и получить точку сопряжения К.
Соединить найденный центр О2 и центр окружности О1 и получить точку сопряжения М.
Из точки O2 радиусом R2 провести дугу сопряжения.

Слайд 36

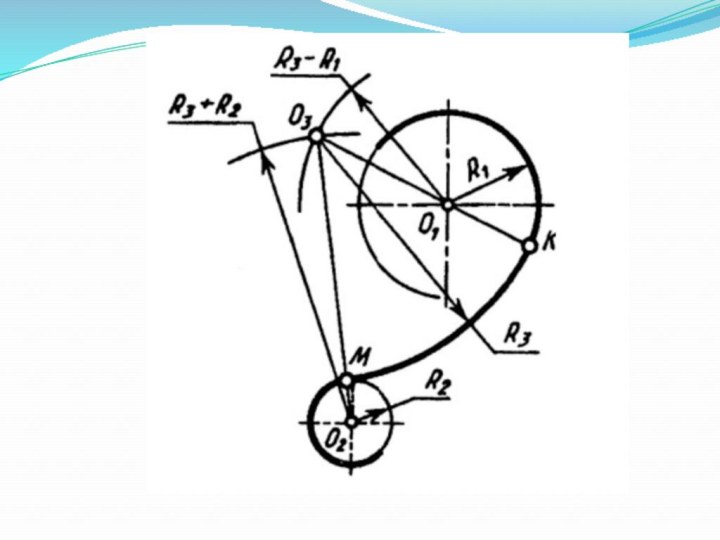
Слайд 37 Из центра O1 данной окружности радиуса R1 провести

Из центра O1 данной окружности радиуса R1 провести дугу вспомогательной окружности

дугу вспомогательной окружности радиуса R1-R2.
Из центра O2 данной окружности

радиуса R2 провести дугу вспомогательной окружности радиуса R1-R2. Точка пересечения этих вспомогательных дуг окружности будет центром дуги сопряжения O2.
Соединить найденный центр О2 и центр окружности О1 и получить точку сопряжения К.
Соединить найденный центр О2 и центр окружности О1 и получить точку сопряжения М.
Из точки O2 радиусом R2 провести дугу сопряжения.

Внутреннее касание:

Слайд 38

Слайд 39 Из центра O1 данной окружности радиуса R1 провести

дугу вспомогательной окружности радиуса R2-R1.
Из центра O1 данной окружности

радиуса R1 провести дугу вспомогательной окружности радиуса R2+R1. . Точка пересечения этих вспомогательных дуг окружности будет центром дуги сопряжения O2.
Соединить найденный центр О2 и центр окружности О1 и получить точку сопряжения К.
Соединить найденный центр О2 и центр окружности О1 и получить точку сопряжения М.
Из точки O2 радиусом R2 провести дугу сопряжения.

Смешанное касание (внутреннее и внешнее).