Слайд 2
Понятия фрактал и фрактальная геометрия, появившиеся в конце

70-х, с середины 80-х прочно вошли в обиход математиков
и программистов. Слово фрактал образовано от латинского fractus и в переводе означает состоящий из фрагментов. Оно было предложено Бенуа Мандельбротом в 1975 году для обозначения нерегулярных, но самоподобных структур, которыми он занимался.
Рождение фрактальной геометрии принято связывать с выходом в 1977 году книги Мандельброта `The Fractal Geometry of Nature'. В его работах использованы научные результаты других ученых, работавших в период 1875-1925 годов в той же области (Пуанкаре, Фату, Жюлиа, Кантор, Хаусдорф). Но только в наше время удалось объединить их работы в единую систему.
Роль фракталов в машинной графике сегодня достаточно велика. Они приходят на помощь, например, когда требуется, с помощью нескольких коэффициентов, задать линии и поверхности очень сложной формы. Фрактальная геометрия незаменима при генерации искусственных облаков, гор, поверхности моря, шероховатой поверхности. Фактически найден способ легкого представления сложных неевклидовых объектов, образы которых весьма похожи на природные.
Одним из основных свойств фракталов является самоподобие. В самом простом случае небольшая часть фрактала содержит информацию о всем фрактале. ВАЖНО!
Определение фрактала, данное Мандельбротом, звучит так: "Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому"
Слайд 3
Фрактал Мандельброта есть множество точек C
на комплексной плоскости, для которых
последовательность Zi,
определяемая итерациями
Z0 = 0,
Z1 = Z02 + C,
Z2 = Z12 + C,
…
Zi+1 = Zi2 + C,
конечна (то есть не
уходит в бесконечность).
Слайд 4
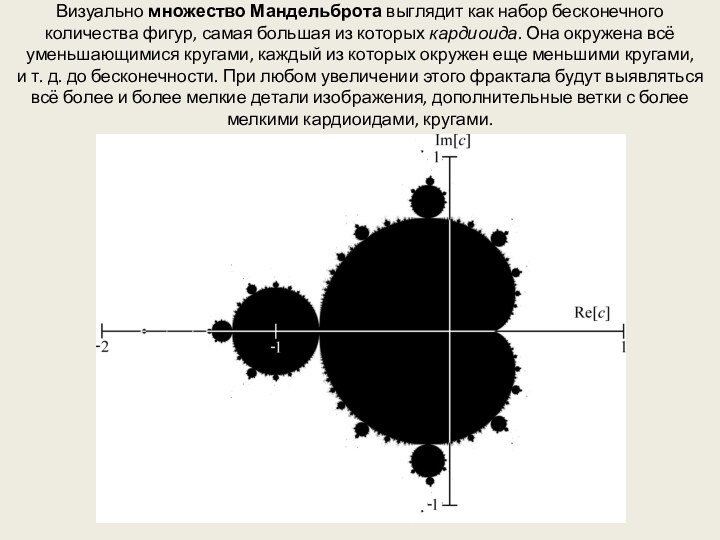
Визуально множество Мандельброта выглядит как набор бесконечного количества
фигур, самая большая из которых кардиоида. Она окружена всё
уменьшающимися кругами, каждый из которых окружен еще меньшими кругами, и т. д. до бесконечности. При любом увеличении этого фрактала будут выявляться всё более и более мелкие детали изображения, дополнительные ветки с более мелкими кардиоидами, кругами.
Слайд 5
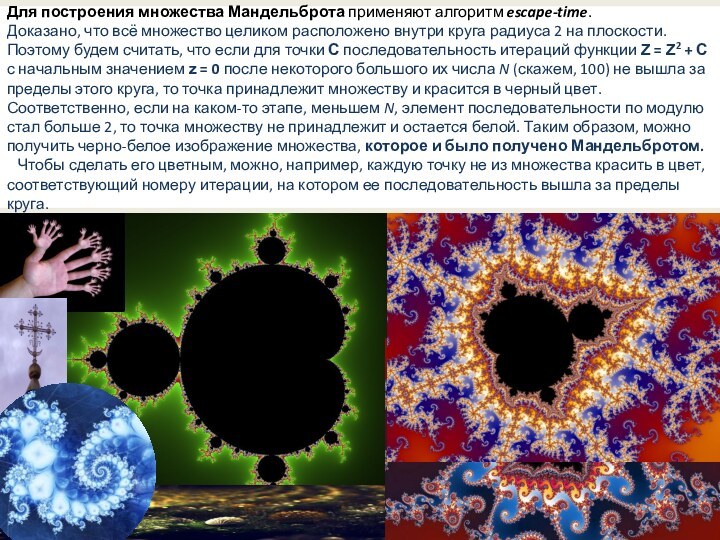
Для построения множества Мандельброта применяют алгоритм escape-time.
Доказано, что
всё множество целиком расположено внутри круга радиуса 2 на плоскости.
Поэтому будем считать, что если для точки C последовательность итераций функции Z = Z2 + C с начальным значением z = 0 после некоторого большого их числа N (скажем, 100) не вышла за пределы этого круга, то точка принадлежит множеству и красится в черный цвет. Соответственно, если на каком-то этапе, меньшем N, элемент последовательности по модулю стал больше 2, то точка множеству не принадлежит и остается белой. Таким образом, можно получить черно-белое изображение множества, которое и было получено Мандельбротом.
Чтобы сделать его цветным, можно, например, каждую точку не из множества красить в цвет, соответствующий номеру итерации, на котором ее последовательность вышла за пределы круга.
Слайд 6
Фильмы о фракталах
http://www.youtube.com/watch?v=pYHSNFNxy50
ПОСМОТРЕТЬ фрактал самому:
http://elementy.ru/posters/fractals/Mandelbrot#nop
Построение фрактала, 7 м
http://video.yandex.ru/users/ksseha/view/7/
Полёт
в глубину фрактала
http://www.youtube.com/watch?v=bO9ugnn8DbE
http://www.youtube.com/watch?v=KOkGEs9JTrI
http://www.youtube.com/watch?v=Pzg4XvaBnT4