Слайд 2
Задача регрессионного анализа
Задача регрессионного анализ (РА) состоит в
построении модели, позволяющей по значениям независимых переменных получать оценки
значений зависимой переменной.
Используется также для выявления связи переменных.
Слайд 3
Типы переменных регрессионной модели
Зависимая (результирующая) – в модели
играет роль функции, значение которой определяется значениями объясняющих переменных.
Независимые
(объясняющие) – в модели играют роль аргументов, определяют значения результирующей переменной. Их называют предикторами, или факторными признаками.
Слайд 4
Типы переменных регрессионной модели
Зависимая переменная:
непрерывная
Независимые переменные
непрерывные,
дискретные,
категориальные
Слайд 8
Формула для прямой линии
Прямая линия описывается линейной функцией
y = a + bx,
Где a – это точка,
в которой прямая пересекает ось y, b – тангенс угла наклона прямой.
Если b>0, то прямая идет «вверх», т.е. с увеличением x увеличивается y. Связь положительна.
Если b<0, то прямая идет «вниз», т.е. с увеличением x уменьшается y. Связь отрицательна.
Если b=0, то прямая идет параллельно оси x (y=a). Изменения x не влияют на значение y. Связь отсутствует.
Слайд 9
Как интерпретировать коэффициент b?
Знак b говорит о направлении
связи.
Значение b показывает, насколько измениться y если x
изменить на единицу.
Например, y = 2 + 5x.
Если x1 = 5, то y1 = 27. Если x2 = 6, то н2 = 32. y2 – y1 = 32 – 27 = 5 = b.
В данном случае b>0, поэтому y растет с увеличением x.
Слайд 10
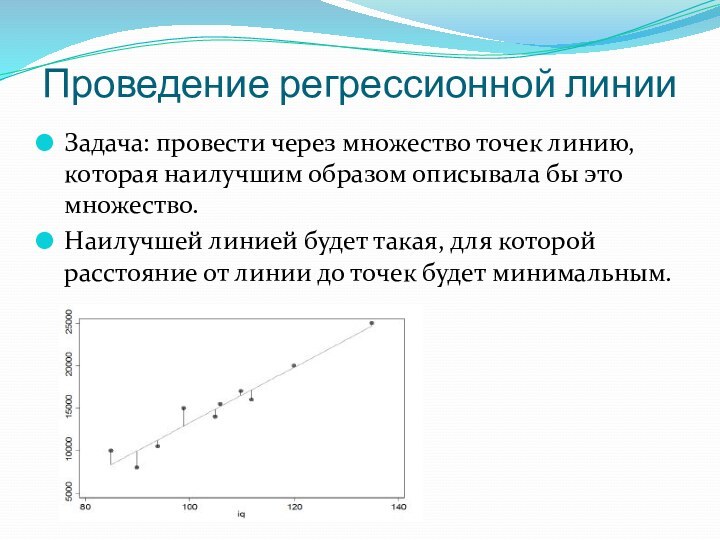
Проведение регрессионной линии
Задача: провести через множество точек линию,
которая наилучшим образом описывала бы это множество.
Наилучшей линией будет
такая, для которой расстояние от линии до точек будет минимальным.
Слайд 11
Метод наименьших квадратов (МНК)
Сумма расстояний будет близка к
нулю, т.к. часть из них являются положительными, часть –
отрицательными величинами. Поэтому:
Можно сложить модули расстояний.
Можно сложить квадраты расстояний. По ряду статистических причин в качестве наилучшего метода для построения регрессионной линии используется метод наименьших квадратов.
Слайд 12
Вернемся к примеры об IQ и доходе
Зарплата =
-19403 + 327 * IQ
a = -19403, b =
327.
Соответственно, согласно этой модели, с увеличением IQ на один пункт зарплата увеличивается на 327 руб. в месяц.
Слайд 13
Ожидаемые значения
Регрессионная формула позволяет определить ожидаемые (предсказанные) значения
y для определённого уровня х.
В примере для IQ =
90 ожидаемое значение зарплаты будет = -19403 + 327*90 = 10027 руб.
Ожидаемые значения y отличаются от реальных значений в базе (у Любы IQ = 90, а зарплата = 8000).
Разница между ожидаемыми и реальными значениями называется остатками (residuals), или ошибками. В случае Любы остаток равен 10027 – 8000 = 2027. Люба получает меньше, чем предсказывает регрессионное уравнение.
Слайд 14
Источники ошибок
Ошибки (остатки) являются неотъемлемой частью регрессионных уравнений.
Случаи, когда одна переменная идеально предсказывает другую (все точки
находятся на регрессионной прямой), являются исключением (и не интересны).
Ошибки состоят из двух компонентов:
Ошибки измерения.
Вероятностный компонент, неизменно присущий отношению между двумя переменными.
Слайд 15
Регрессия – вероятностная модель
Формула регрессионной функции:
E(y) = a
+ βx, где E(y) – ожидаемое значение (среднее) y
на определенном уровне x.
Иначе эту же формулу можно записать так:
y = a + βx + ε, где ε – ошибка.
Слайд 16
Значимость и сила связи
Значимость и сила статистической связи
– два разных понятия.
Значимость: действительно ли x и
y связаны?
Сила: как сильно связаны x и y?
Размер коэффициента b говорит о силе связи. Однако его интерпретация сильно зависит от единиц измерения x. Например, если в нашем примере IQ/10, то коэффициент b уменьшится в 10 раз.
Следовательно, коэффициенты при разных переменных НЕЛЬЗЯ непосредственно сравнивать (но можно сравнивать, если переменные измерены по одной и той же шкале).
Слайд 17
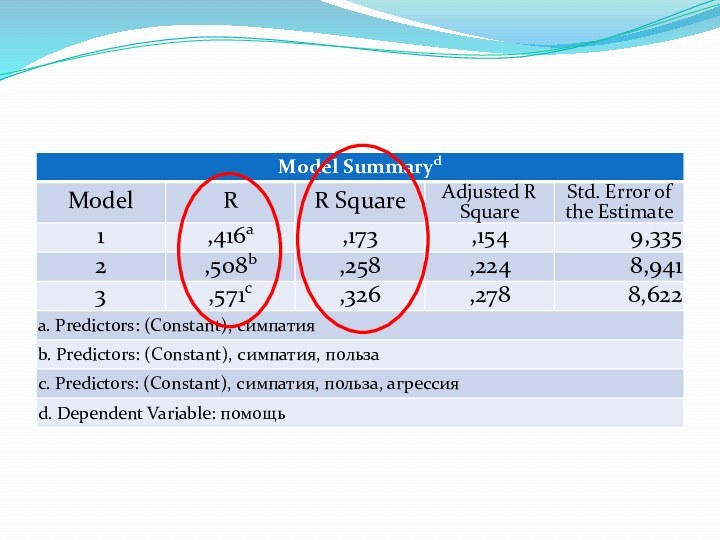
Коэффициент детерминации R-квадрат
R-квадрат является квадратом коэффициента корреляции
R-квадрат принимает
значения от 0 до 1.
1 указывает на идеальную
связь, 0 – на отсутствие связи. Чем больше значение, тем сильнее связь.
R-квадрат можно интерпретировать как долю дисперсии зависимой переменной, которую «объясняет» независимая переменная.
R-квадрат имеет смысл, только когда речь идет о линейной связи.
Слайд 18
Статистическая связь и причинность
Наличие статистической связи не означает
наличия причинной связи между переменными и не позволяет утверждать,
что зависимая переменная влияет на независимую.
Слайд 19
Условия использования РА
Все переменные должны быть случайными, подчиняться
нормальному распределению.
Линейная регрессия используется тогда(и только тогда!), когда зависимая
переменная является интервальной(метрической).
Зависимость между переменными является линейной.
Математическое ожидание остатков должно приближаться к нулю, т.е. они должны быть нормально распределены.
Отсутствие связи между зависимыми переменными (отсутствие мультиколлинеарности).
Слайд 20
Методы устранения или уменьшения мультиколлинеарности
Исключение одного из двух
сильно связанных факторов.
Переход от первоначальных факторов к их главным
компонентам.
Использование стратегии шагового отбора факторов.
Слайд 21
Построение модели
Качество результатов регрессионного анализа определяется качеством теоретического
обоснования спецификации модели.
Как выбирать переменные для включения в модель?
Теоретическая логика
Эксплораторная логика
Следует избегать стратегии «мусорной корзины».
Слайд 22
Этапы построения модели регрессии
Проверка распределения всех переменных на
нормальность
Проверка объясняющих переменных на наличие мультиколлинеарности
Построение линейного уравнения регрессии
Оценка
качества модели
Построение прогноза по модели регрессии
Слайд 23
1. Проверка распределения всех переменных на нормальность
Критерий Колмогорова-Смирнова
Переменные,
не являющиеся нормально распределенными, не могут использоваться в модели
Слайд 24
2. Проверка объясняющих переменных на наличие мультиколлинеарности
Анализ матрицы
коэффициентов парной корреляции
Если коэффициент парной корреляции между двумя переменными
больше 0.8, то явление мультиколлинеарности можно считать установленным
Слайд 25
Методы устранения или уменьшения мультиколлинеарности
Исключение одного из двух
сильно связанных факторов.
Переход от первоначальных факторов к их главным
компонентам.
Использование стратегии шагового отбора факторов.
Слайд 26
3. Построение линейного уравнения регрессии
Analyze – Regression –
Linear…
Слайд 27
4. Оценка качества модели
Коэффициент детерминации R2 (Доля вариации
результативного признака под воздействием изучаемых факторов)
Коэффициент множественной корреляции R
(теснота связи зависимой переменной со всеми включенными в модель объясняющими факторами)
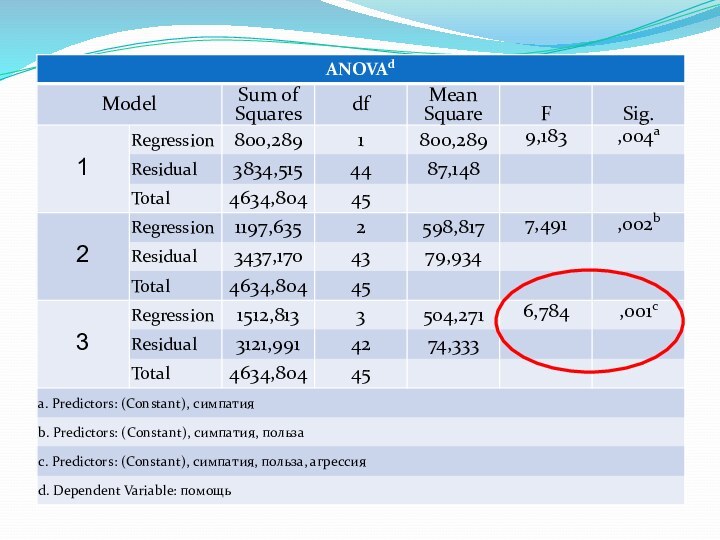
F-критерий Фишера (Проверка значимости уравнения регрессии)
Слайд 30
4. Оценка качества модели-2
Проверка распределение остатков
Критерий Колмогорова-Смирнова
Слайд 31
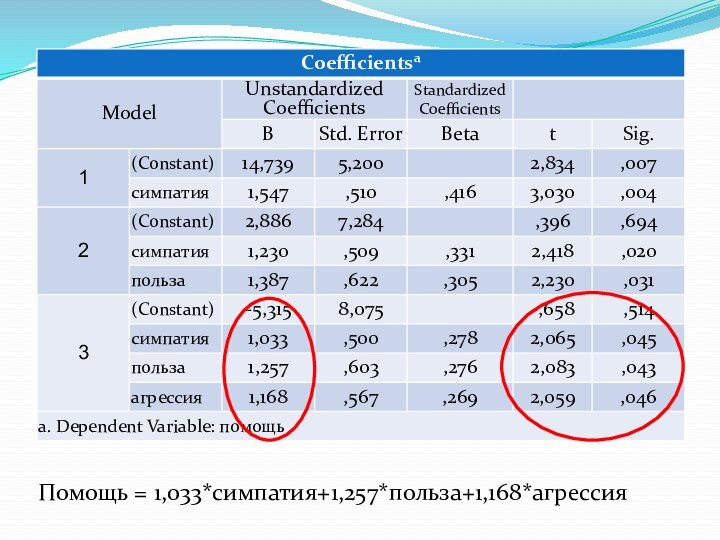
5. Построение прогноза по модели регрессии
Необходимо построить регрессионное
уравнение