- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Эффект Мёссбауэра
Содержание
- 2. ВведениеОткрыт в 1958 году.Эффект является ядерным аналогом
- 3. До 1958 г. наблюдение резонансного поглощения γ-квантов
- 4. Рис.1. Схема энергетических уровней ядраЭнергия отдачи ER
- 5. Для обычной оптической резонансной флюоресценции это условие
- 6. Резонансное поглощение не идет на свободных ядрах.
- 7. Основная идея МёссбауэраВ квантовой механике эффект кристаллической
- 8. При таких переходах без отдачи и происходит
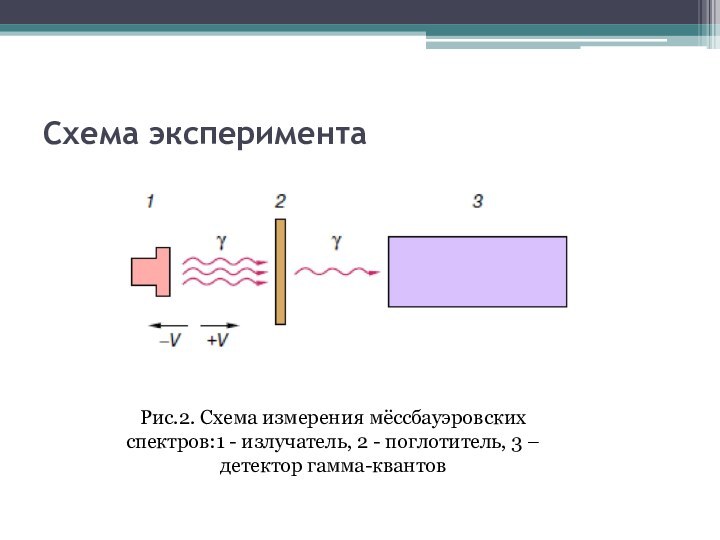
- 9. Схема экспериментаРис.2. Схема измерения мёссбауэровских спектров:1 - излучатель, 2 - поглотитель, 3 – детектор гамма-квантов
- 10. Имеется источник монохромных гамма-квантов, представляющий собой вещество,
- 11. Гамма-кванты, испускаемые излучателем, попадают на поглотитель. Те
- 12. Для того, чтобы получить спектральную линию (зависимость
- 13. Если излучатель и поглотитель неподвижны один относительно
- 14. Рис. 3. Мёссбауэровский спектр (а) и схема
- 15. Ширина экспериментального спектра, определяемая на полувысоте линии
- 16. КОЭФФИЦИЕНТ МЁССБАУЭРА Выше мы рассматривали ядра, жестко
- 17. В реальном твердом теле атомные ядра совершают
- 18. Чем выше температура тела, тем больше в
- 19. Изомерный сдвигЕсли излучатель и поглотитель содержат одни
- 20. Наличие разности в энергии перехода для излучателя
- 21. Рис. 4. Мёссбауэровский спектр (а) и схема
- 22. На рис. 4 представлен в качестве примера
- 23. МАГНИТНОЕ РАСЩЕПЛЕНИЕ МЁССБАУЭРОВСКИХ СПЕКТРОВ Энергия ядра может
- 24. При классическом описании скалярное произведение векторов магнитного
- 25. В частности, основное состояние ядер 57Fe и
- 26. Скачать презентацию
- 27. Похожие презентации
ВведениеОткрыт в 1958 году.Эффект является ядерным аналогом резонансной флюоресценции и состоит в том, что если одно ядро испускает γ-квант, то другое такое же ядро с большей вероятностью поглощает этот квант.























Слайд 3 До 1958 г. наблюдение резонансного поглощения γ-квантов ядрами
считалось невозможным, т.к. при вылете фотона ядро получает импульс
отдачи p, равный по величине импульсу фотона pя=-pγ=p; |pγ | = Eγ/c.Соответственно ядро приобретает кинетическую энергию ER=p2/2M, где M – масса ядра.
Поэтому энергия cp вылетающего фотона не точно равна энергии перехода E (т.е. разности уровней ядра), а связана с ней соотношением E= Eγ+ER, учитывающим, что энергия перехода делится между фотоном и ядром отдачи.
Слайд 4
Рис.1. Схема энергетических уровней ядра
Энергия отдачи ER с
хорошей точностью определяется формулой ER= Eγ2/2Mc2
Т.е. баланс энергии выражается
соотношением: Eγ = E - ER = E - Eγ2/2Mc2
Но Eγ/Mc2 мало, значит:
Eγ ≈ E - E2/2Mc2
ER ≈ E2/2Mc2
Пусть на переходе A→B гамма-квант поглощается. Тогда энергия поглощаемого кванта Eγп должна быть Eγп = E + ER.
Слайд 5 Для обычной оптической резонансной флюоресценции это условие баланса
энергии прекрасно выполняется.
Но для ядерного излучения это условие
нарушается, причем очень сильно, из-за того, что ER квадратично растет с энергией кванта, а энергии ядерных γ-квантов на несколько порядков больше энергий оптических фотонов. Слайд 6 Резонансное поглощение не идет на свободных ядрах. По
законам классической механики при переходе от свободных ядер к
твердому телу – кристаллу – ситуация не изменится. Под влиянием сил кристаллических связей эффект отдачи смягчится, но резонанса не будет.Амплитуда отдачи столь мала, что необходимо не классическое, а квантовое рассмотрение.
Слайд 7
Основная идея Мёссбауэра
В квантовой механике эффект кристаллической связи
проявляется статистическим образом, т.е. не так, как в классической.
Влияние кристаллической решетки мало в среднем.
В большинстве случаев ядра испытывают полную отдачу. В небольшом проценте случаев идут переходы без отдачи, в которых импульс фотона принимает на себя не отдельное ядро, а кристалл в целом.
Слайд 8
При таких переходах без отдачи и происходит резонансное
поглощение. Возможность наблюдения такого поглощения зависит от того, какой
процент переходов происходит без отдачи.Возможность наблюдения такого поглощения зависит от того, какой процент переходов происходит без отдачи.
Чем ниже энергия перехода и чем ниже температура кристалла, тем благоприятнее условия для перехода без отдачи.
Требуется глубокое охлаждение образца.
Слайд 9
Схема эксперимента
Рис.2. Схема измерения мёссбауэровских спектров:1 - излучатель,
2 - поглотитель, 3 – детектор гамма-квантов
Слайд 10 Имеется источник монохромных гамма-квантов, представляющий собой вещество, содержащее
короткоживущие изомеры определенных изотопов, например 57mFe и 119mSn для
изотопов 57Fe и 119Sn с временами жизни 140 и 25,4 нс соответственно.Затем ставится поглотитель — вещество, содержащее тот же самый изотоп, что и излучатель, а за ним детектор гамма-квантов.
Слайд 11
Гамма-кванты, испускаемые излучателем, попадают на поглотитель. Те из
них, энергия которых совпадает с разностью энергий возбужденного и
основного состояний ядер изотопа в поглотителе, возбуждают ядро, поглощаясь при этом, и не попадают на детектор.Кванты же других частот проходят через поглотитель свободно и регистрируются детектором.
Слайд 12 Для того, чтобы получить спектральную линию (зависимость поглощаемых
гамма-квантов от энергии), необходимо изменять энергию гамма-квантов излучателя. Поскольку
спектральные линии в эффекте Мёссбауэра очень узкие, девиация (изменение) частоты гамма-квантов излучателя должна быть небольшой. Для этого используют эффект Доплера — зависимость частоты излучения электромагнитной энергии от скорости движения источника излучения.При мёссбауэровских измерениях излучатель движется со скоростью ±V, поэтому вместо энергии или частоты по оси абсцисс откладывают скорость (обычно в мм/с), которая легко переводится в частоту или энергию, как будет показано ниже.
Слайд 13 Если излучатель и поглотитель неподвижны один относительно другого,
то в поглотителе реализуется условие резонансного поглощения гамма-квантов, испускаемых
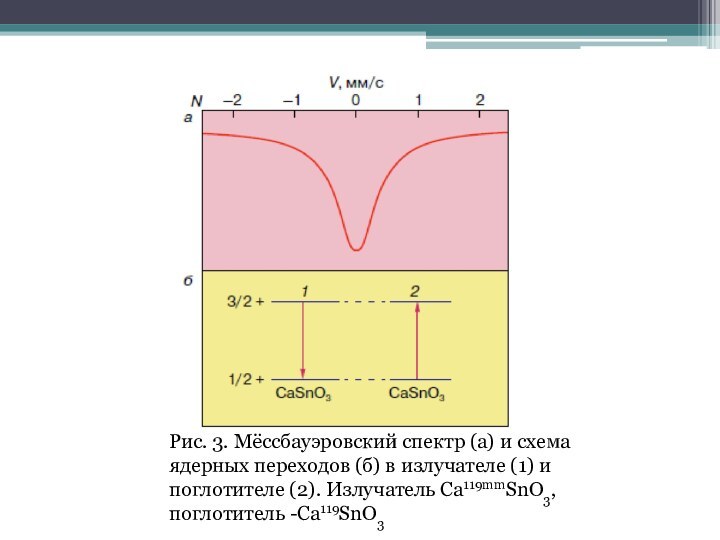
излучателем. Если же излучатель движется со скоростью ± V, то энергия испускаемых излучателем гамма-квантов за счет эффекта Доплера будет меняться в пределах ∆E=± Е0*V/c , где Е0 — разность энергий между возбужденным и основным состояниями мёссбауэровского ядра (энергия изомерного перехода); c — скорость света. Следовательно, часть гамма-квантов, испускаемых излучателем, энергия которых отличается от Е0, будет свободно проходить через поглотитель. Зависимость скорости счета N детектора от скорости движения источника V и называется мёссбауэровским спектром.Слайд 14 Рис. 3. Мёссбауэровский спектр (а) и схема ядерных
переходов (б) в излучателе (1) и поглотителе (2). Излучатель
Ca119mmSnO3, поглотитель -Ca119SnO3Слайд 15 Ширина экспериментального спектра, определяемая на полувысоте линии Гэксп=2Г,
Г=h/t, t-время жизни короткоживущего изотопа в возбужденном состоянии. То
есть экспериментальный спектр должен иметь ширину, равную удвоенной естественной ширине спектральной линии.Это связано с тем, что форма линии мёссбауэровского спектра является результатом наложения линий излучателя и поглотителя.
Слайд 16
КОЭФФИЦИЕНТ МЁССБАУЭРА
Выше мы рассматривали ядра, жестко закрепленные
в твердом теле. Если же ядро свободно, то излучение
гамма-кванта сопровождается появлением энергии отдачи ядра ER=E02/2Mc2, где М — масса ядра. В этом случае гамма-квант имеет энергию, отличную от энергии изомерного перехода на величину ER:ħω=E0-ER.
Обычно энергия отдачи равна приблизительно 10-2 эВ, но этого достаточно для того, чтобы резонансное поглощение исчезло. Поэтому эффект Мёссбауэра и наблюдается только в твердых телах.
Слайд 17 В реальном твердом теле атомные ядра совершают тепловое
колебательное движение относительно некоторого равновесного положения. Поэтому более адекватной
является модель твердого тела, согласно которой кристалл представляет собой совокупность жестко закрепленных осцилляторов, энергия колебательного движения каждого из которых может быть записана в виде E = ħω (n + 1/2),где ω — частота колебаний, n = 0, 1, 2, ...Увеличение (уменьшение) n на единицу рассматривается как исчезновение (появление) фонона — кванта тепловых колебаний кристаллической решетки. В связи с этим наряду с безотдачным испусканием (поглощением) гамма-квантов в твердом теле будут излучаться и гамма-кванты, энергия которых отличается от энергии изомерного перехода на ± ħω, ± 2 ħω и т.д.
Слайд 18 Чем выше температура тела, тем больше в нем
фононов. Следовательно, с повышением температуры число безотдачных гамма-квантов уменьшается.
Вероятность испускания f (поглощения f*) гамма-квантов без отдачи и называется коэффициентом Мёссбауэра.Этот коэффициент всегда меньше единицы, поэтому даже при неподвижном излучателе при измерениях мёссбауэровских спектров скорость счета детектора будет отлична от нуля (детектор регистрирует гамма-кванты, испускаемые с отдачей и прошедшие через поглотитель). Очевидно, что чем выше температура, тем меньше коэффициент Мёссбауэра.
Слайд 19
Изомерный сдвиг
Если излучатель и поглотитель содержат одни и
те же изотопы, но их электронные структуры различны, то
энергии переходов для ядра источника гамма-квантов и ядра-поглотителя оказываются также различными. Это обусловлено тем, что энергии основного и возбужденного состояний атомного ядра кроме всего прочего определяются и электронно-ядерным (сверхтонким) взаимодействием.В результате любая перестройка внешней оболочки мёссбауэровского атома приводит к изменению энергии испускаемых (поглощаемых) гамма-квантов.
Слайд 20 Наличие разности в энергии перехода для излучателя и
поглотителя приводит к тому, что при неподвижном излучателе не
наблюдается резонансного поглощения гамма-квантов в поглотителе.Для того, чтобы зарегистрировать мёссбауэровский спектр в этом случае, необходимо изменить энергию гамма-квантов, испускаемых излучателем, что достигается движением излучателя со скоростью ± V, то есть использованием эффекта Доплера.
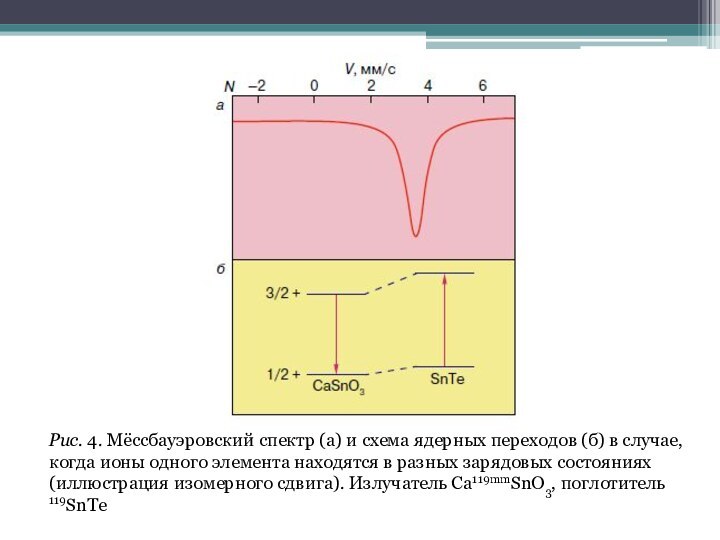
Слайд 21 Рис. 4. Мёссбауэровский спектр (а) и схема ядерных
переходов (б) в случае, когда ионы одного элемента находятся
в разных зарядовых состояниях (иллюстрация изомерного сдвига). Излучатель Са119mmSnO3, поглотитель 119SnTeСлайд 22 На рис. 4 представлен в качестве примера мёссбауэровский
спектр изотопа олова 119Sn для излучателя Ca119mmSnO3 и поглотителя
119SnTe. В излучателе олово находится в зарядовом состоянии Sn4+, а в поглотителе — Sn2+.В результате центр линии мёссбауэровского спектра поглотителя сдвинут относительно исходного перехода на V= 3,55 мм/c. Этот сдвиг и называется изомерным сдвигом мёссбауэровского спектра. Таким образом, мы приходим к выводу, что по величине изомерного сдвига при известном зарядовом состоянии мёссбауэровских атомов в излучателе можно определить зарядовое состояние аналогичных атомов в поглотителе.
Слайд 23
МАГНИТНОЕ РАСЩЕПЛЕНИЕ МЁССБАУЭРОВСКИХ СПЕКТРОВ
Энергия ядра может изменяться
в результате магнитного взаимодействия. Если в месте расположения ядра
действует магнитное поле В, а ядро имеет отличный от нуля магнитный момент μ, то энергия ядра в магнитном поле равна Eм=μВРис. 5. Магнитная структура мёссбауэровского спектра (а) и схема ядерных переходов (б) в присутствии магнитного поля на ядре. Излучатель 57Со, поглотитель - железо 57Fe
Слайд 24 При классическом описании скалярное произведение векторов магнитного момента
и магнитного поля может принимать любые значения от μВ
до -μВ, то есть энергия ядра может изменяться непрерывно.На самом деле это изменение энергии ядра в магнитном поле квантуется, то есть может принимать лишь значения, определяемые проекцией спина ядра I на направление магнитного поля. При этом число энергетических уровней равно 2I + 1.
Слайд 25 В частности, основное состояние ядер 57Fe и 119Sn
со спином 1/2 расщепляется на два, а возбужденное (I
= 3/2) — на четыре подуровня, как показано на рис. 5.Правила отбора разрешают переходы между подуровнями основного и возбужденного состояний только с изменением проекции спина на ± 1.
Эти переходы на рис. 5 отмечены стрелками. Соответственно в мёссбауэровском спектре наблюдаются шесть линий с отношением интенсивностей 3 : 2 : 1 : 1 : 2 : 3.





























