- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Геометрические Векторы
Содержание
- 2. Операции над векторамиСЛОЖЕНИЕОперацию сложения геометрических векторов можно
- 3. Правило треугольникаДля сложения двух векторов a и
- 4. Правило параллелограмма Для сложения двух векторов a
- 5. Сложение векторов с использованием координат.Каждая координата суммы
- 6. Модуль(длинна)ВектораМодуль(длинну)вектора можно узнать например при помощи теоремы
- 7. р
- 8. Скачать презентацию
- 9. Похожие презентации
Операции над векторамиСЛОЖЕНИЕОперацию сложения геометрических векторов можно определить несколькими в принципе эквивалентными способами, каждый из которых однако может быть удобнее или естественнее в зависимости от ситуации и типа рассматриваемых векторов. Так, правило треугольника наиболее простое и
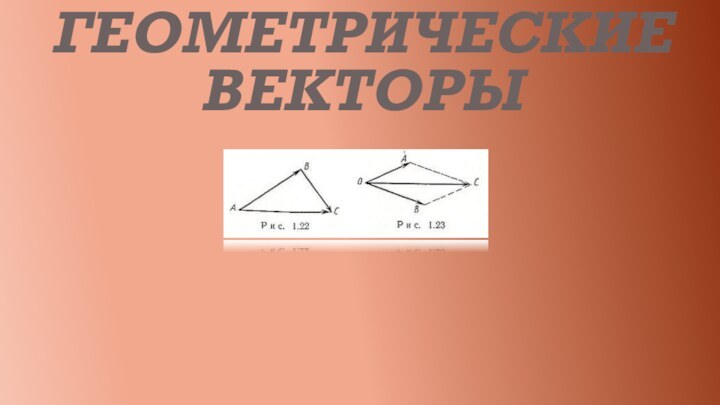







Слайд 3
Правило треугольника
Для сложения двух векторов a и b
по правилу треугольника оба эти вектора переносятся параллельно самим
себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора Это правило прямо и естественно обобщается для сложения любого количества векторов, переходя в правило ломаной: начало второго вектор совмещается с концом первого, начало третьего — с концом второго и т. д., сумма же nвекторов есть вектор, с началом, совпадающим с началом первого, и концом, совпадающим с концом n-го (то есть изображается направленным отрезком, замыкающим ломаную).Для сложения двух векторов и
Слайд 4
Правило параллелограмма
Для сложения двух векторов a и
b по правилу параллелограмма оба эти векторы переносятся параллельно самим себе
так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала
Слайд 5
Сложение векторов с использованием координат.
Каждая координата суммы векторов
есть сумма соответствующей координаты всех (двух или более) суммируемых
векторов. Например, для двумерного случая:
Слайд 6
Модуль(длинна)Вектора
Модуль(длинну)вектора можно узнать например при помощи теоремы косинусов
Где
— угол между отрезками, изображающими
данные векторы, когда начало одного вектора совпадает с концом другого.Или:
Где — угол между векторами (выходящими из одной точки).





























