- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Глава 1Излучение и вещество
Содержание
- 2. 1.1 Кинетическая теория свободных частицГлава 1. Излучение и вещество
- 3. Глава 1. Излучение и веществоУравнения состояния можно
- 4. Глава 1. Излучение и веществоДля изотропного распределения
- 5. 1.2 Функция распределения фермионов и бозонов по энергиямГлава 1. Излучение и вещество
- 6. Глава 1. Излучение и веществоФермионы – полуцелый
- 7. Функция распределения для невырожденных частицГлава 1. Излучение
- 8. Глава 1. Излучение и веществоКритерий вырождения для
- 9. Глава 1. Излучение и веществоПараметр вырождения определяется
- 10. Характерные астрофизические случаиГлава 1. Излучение и веществоДля
- 11. 1.3 Функция распределения Планка для фотоновГлава 1. Излучение и вещество
- 12. Глава 1. Излучение и веществоДля фотонов число
- 13. Глава 1. Излучение и вещество
- 14. 1.4 Уравнение состоянияГлава 1. Излучение и вещество
- 15. Глава 1. Излучение и веществоКлассический газНерелятивистский вырожденный Ферми-газ
- 16. Глава 1. Излучение и веществоРелятивистский вырожденный Ферми-газ (pF»m0c2 , pv(p) = pc(1 − m0c2/2p2) )Фотоны:
- 17. Глава 1. Излучение и веществоОбобщенная диаграмма Температура
- 18. 1.5 Излучение. Базовые понятияГлава 1. Излучение и вещество
- 19. Глава 1. Излучение и веществоИнтенсивность Iν [эрг
- 20. Глава 1. Излучение и вещество Плотность излучения
- 21. 1.6 Переходы в атомах и молекулахГлава 1. Излучение и вещество
- 22. Глава 1. Излучение и вещество
- 23. Глава 1. Излучение и веществоСпектрДискретный (связанные электроны)Непрерывный
- 24. Глава 1. Излучение и веществоУширение и профиль
- 25. 1.7 Перенос излученияГлава 1. Излучение и вещество
- 26. Глава 1. Излучение и веществоКоэффициент поглощенияпрохождение излучения
- 27. Глава 1. Излучение и веществоκν(T, ρ) как
- 28. Глава 1. Излучение и веществоКоэффициент излученияпорождение излучения в среде (не зависит от Iν)εν = εν(ρ,T)
- 29. Глава 1. Излучение и веществоУравнение переноса излученияоднородное
- 30. Глава 1. Излучение и веществоПеренос излучения при
- 31. 1.8 Линии излучения и поглощенияГлава 1. Излучение и вещество
- 32. Глава 1. Излучение и вещество
- 33. Глава 1. Излучение и вещество
- 34. Глава 1. Излучение и веществоПрименимость ЛТР
- 35. Скачать презентацию
- 36. Похожие презентации

















![Глава 1Излучение и вещество Глава 1. Излучение и веществоИнтенсивность Iν [эрг см−2с−1Гц−1страд-1 ] Iν = const](/img/tmb/13/1278963/07057b3e6e629fb01b0c436e0d3b15f5-720x.jpg)
![Глава 1Излучение и вещество Глава 1. Излучение и вещество Плотность излучения ρν [эрг см-3 Гц-1] Светимость](/img/tmb/13/1278963/94ad58ca37735b3dce636b6844f18508-720x.jpg)











Слайд 3
Глава 1. Излучение и вещество
Уравнения состояния можно получить
с использованием кинетической теории, как соответствующие моменты функции распределения
частиц по энергиямДля изотропной функции распределения частиц по импульсам n(p) в кубе с объемом L3 с числовой плотностью n0 = N/L3 выполняется условие нормировки:
Давление P определяется как перенесенный импульс за время dt через площадку L2:
Term1 – импульс, переносимый одной частицей; Term2 – общее число частиц, проходящих за dt через площадку; Term3 – плотность числа частиц с импульсом p.
Слайд 4
Глава 1. Излучение и вещество
Для изотропного распределения частиц
в сферической СК:
Давление определяется как момент от функции распределения
частиц по импульсамАналогично:
где ε = p2/2m или
Слайд 6
Глава 1. Излучение и вещество
Фермионы – полуцелый спин
(электроны, нейтроны, протоны); бозоны – целый спин (фотоны). При
высоких температурах и низкой плотности поведение не отличается (идеальный газ)Е – энергия частицы
dN – число частиц в диапазоне (E, E+dE)
dg = α d3x d3p/h3 – количество квантовых состояний в диапазоне (E, E+dE),
α – мультипликативность (мультиплетность), определяемая спином α=2s+1
+1 – фермионы (действует принцип запрета Паули: только одна частица в фазовой ячейке)
-1 – бозоны (принцип Паули не действует)
η – параметр вырождения ([хим. потенциал μ]/kT) [dU = TdS − PdV + μdN]
Для систем частиц, обладающих массой покоя (частицы не возникают и не уничтожаются),
η определяется из закона сохранения
Для фотонов N не сохраняется и η = 0.
Слайд 7
Функция распределения для невырожденных частиц
Глава 1. Излучение и
вещество
уравнение Максвелла
Функция распределения по энергиям невырожденных частиц для случая
ТР
Слайд 8
Глава 1. Излучение и вещество
Критерий вырождения для газа
частиц
длина волны де Бройля для частицы
r0 – среднее расстояние
между частицаминевырожденный случай
Критерий невырожденности (η << -1): r0 >> λdeBroglie
В астрофизике вырождаются обычно фермионные системы:
α/h3 – максимальная фазовая плотность (одна частица на фазовую ячейку)
Для нерелятивистских фермионов с ε = p2/2m
Система фермионов вырождается, когда температура << хим. потенциала, в таком случае f(ε) = 0 при μ = εF (энергия Ферми (наибольшая энергия частиц в системе) и соответствующий ей импульс Ферми pF)
Слайд 9
Глава 1. Излучение и вещество
Параметр вырождения определяется из
нормировки на сохранение полного числа частиц в системе:
Для однородного
и изотропного распределения частиц в фазовом пространстве:Решая относительно η и выражая через λdeBroglie и r0, получим
Слайд 10
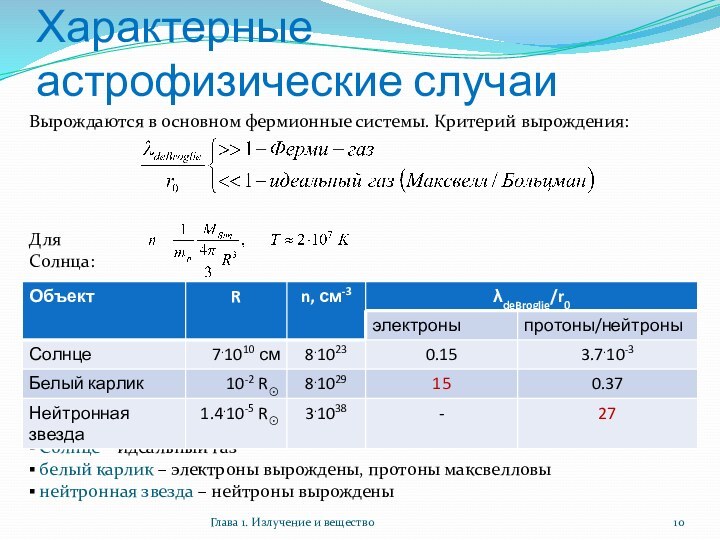
Характерные астрофизические случаи
Глава 1. Излучение и вещество
Для Солнца:
Солнце – идеальный газ
белый карлик – электроны вырождены,
протоны максвелловынейтронная звезда – нейтроны вырождены
Вырождаются в основном фермионные системы. Критерий вырождения:
Слайд 12
Глава 1. Излучение и вещество
Для фотонов число частиц
не сохраняется, η = 0
для изотропного распределения и двух
возможных поляризацийгде интенсивность Bν – энергия, проходящая через единичную поверхность в единицу времени в единичном телесном угле
функция Планка
закон
Стефана-Больцмана
приближение Рэлея-Джинса
приближение Вина
плотность энергии
Слайд 16
Глава 1. Излучение и вещество
Релятивистский вырожденный Ферми-газ (pF»m0c2
, pv(p) = pc(1 − m0c2/2p2) )
Фотоны:
Слайд 17
Глава 1. Излучение и вещество
Обобщенная диаграмма Температура –
Плотность
Обычные звезды:
P = nkT, ρ = μmpn,
Ukin = 3/2·P (μ = ρ/(mpn) – молекулярный вес)
Белые карлики:
давление вырожденных электронов
n = ne, ρ = μempne, μe = zμ, где z – число свободных электронов на атом
нерелятивистское вырождение
(ρ < 106 г см−3):
P = A1ρ5/3, Ukin= 3/2·P
релятивистское вырождение
(ρ > 106 г см−3):
P = A2(ρ4/3− B2ρ2/3),
P = 1/3·Ukin(1 + C2ρ−1/3)
Нейтронные звезды:
давление вырожденных нейтронов
n = nn, ρ = nmn
Уравнение состояния аналогично БК, но с иными A, B и ρcr
Слайд 19
Глава 1. Излучение и вещество
Интенсивность Iν [эрг см−2с−1Гц−1страд-1
]
Iν = const в отсутствие поглощения или излучения
в евклидовом пространстве
Поток энергии излучения Fν [эрг см-2 c-1 Гц-1]
Слайд 20
Глава 1. Излучение и вещество
Плотность излучения ρν
[эрг см-3 Гц-1]
Светимость Lν [эрг с-1]
Эффективная температура
Teff
Слайд 23
Глава 1. Излучение и вещество
Спектр
Дискретный (связанные электроны)
Непрерывный (свободные
электроны)
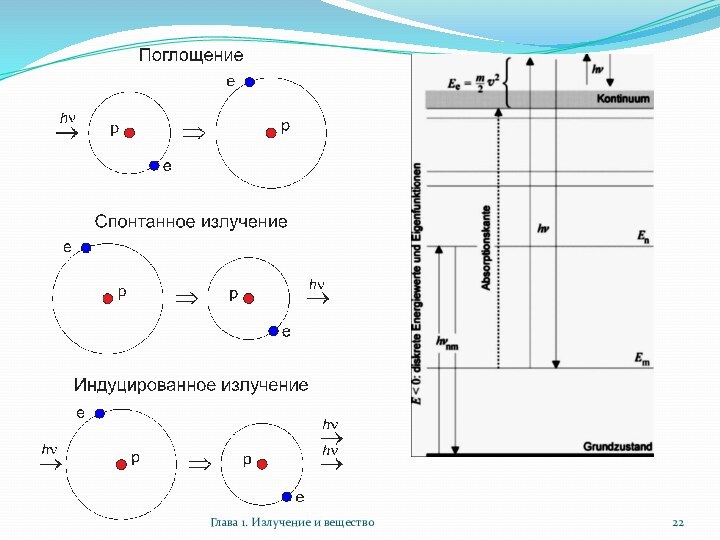
Взаимодействия между фотонами и электронами (в т.ч. связанными в
атомах и молекулах) ведут кпоглощению (dn = nlBluρludt)
спонтанному излучению (dn = nuAuldt)
вынужденному излучению (dn = nuBulρludt)
Возможные типы переходов:
связано-связанные (спектральные линии)
свободно-связанные (ионизационный/рекомбинационный континуум)
свободно-свободные (тормозное излучение в поле ионов)
полные вероятности переходов
Слайд 24
Глава 1. Излучение и вещество
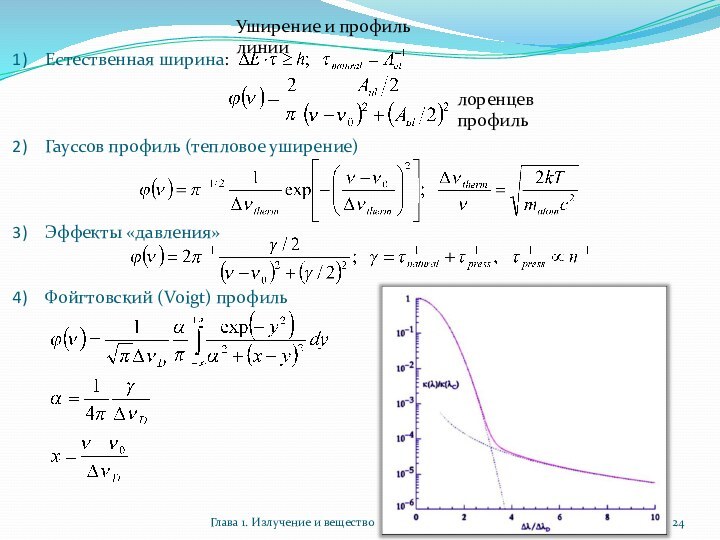
Уширение и профиль линии
Естественная
ширина:
Гауссов профиль (тепловое уширение)
Эффекты «давления»
Фойгтовский (Voigt) профиль
лоренцев профиль
Слайд 26
Глава 1. Излучение и вещество
Коэффициент поглощения
прохождение излучения через
среду с поглощением
вероятность поглощения фотона одиночным атомом
число поглощений в
dVСвязь между макро и микро параметрами среды
с учетом вынужденного излучения («просветление» среды)
свободно-связанные
линии
свободно-свободные
α – элемент
β – степень ионизации
bγα,β= nγα,β(NLTE) / nγα,β(LTE) ≈1
Слайд 27
Глава 1. Излучение и вещество
κν(T, ρ)
как правило
в
сравнительно узких интервалах ρ и T
κ/ρ [м2/частицу] от длины
волны в нм для Солнца (слева) Т=5000 К и τSco, T=28000 K
Слайд 28
Глава 1. Излучение и вещество
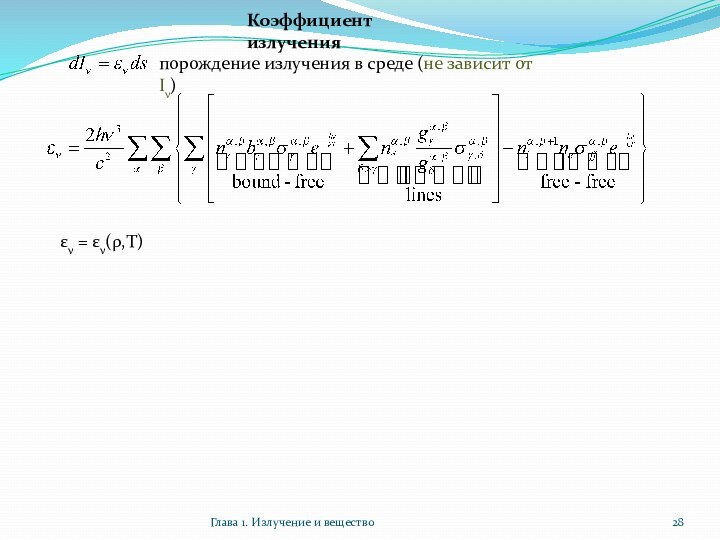
Коэффициент излучения
порождение излучения в
среде (не зависит от Iν)
εν = εν(ρ,T)
Слайд 29
Глава 1. Излучение и вещество
Уравнение переноса излучения
однородное ДУ
1-го порядка, решается аналитически при известных κ и ε,
в том случае, если они не зависят от Iνоптическая толщина среды
(безразмерная характеристика оптических свойств и геометрических размеров среды)
Sν – функция источника
Формальное решение
Слайд 30
Глава 1. Излучение и вещество
Перенос излучения при термодинамическом
равновесии
закон Кихгофа
При ТР Iν= Bν(T) и dIν/ds = 0
Локальное термодинамическое равновесие (ЛТР):
Максвеллово распределение по скоростям с одним значением T
Неупругие столкновения доминируют над радиативными процессами (числовая плотность не слишком мала, т. е. распределение по уровням энергии описывается соотношениями Больцмана и Саха, Sν= Bν(T) = εν/κν)
Приближение ЛТР хорошо работает в звездных атмосферах, в сравнительно малых объемах среды (T = const)





























