- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему ГМТ-1. Геометрическое место точек, равноудаленных от двух данных точек, есть плоскость, перпендикулярная к отрезку с концами в данных точках и проходящая через его середину.
Содержание
- 2. ГМТ-2. Геометрическое место точек, равноудаленных от двух
- 3. ГМТ-3. Геометрическое место точек, равноудаленных от граней
- 4. ГМТ-4. Геометрическое место точек, равноудаленных от всех
- 5. Описанные шарыСфера называется описанной около многогранника, если
- 6. Призма вписанная в шарТеорема. Шар можно описать
- 7. Следствие 1. Центр шара, описанного около прямой
- 8. Пирамида вписана в шарТеорема. Около пирамиды можно
- 9. Следствие 1. Центр шара, описанного около пирамиды,
- 10. Вписанные шарыСфера называется вписанной в многогранник, если
- 11. Шар вписан в пирамидуТеорема. Если боковые грани
- 12. Следствие 1. Центр шара, вписанного в пирамиду,
- 13. Шар вписан в призмуТеорема. Шар можно вписать
- 14. Скачать презентацию
- 15. Похожие презентации
ГМТ-2. Геометрическое место точек, равноудаленных от двух параллельных между собой плоскостей, есть плоскость, параллельная данным и проходящая через середину расстояния между ними.
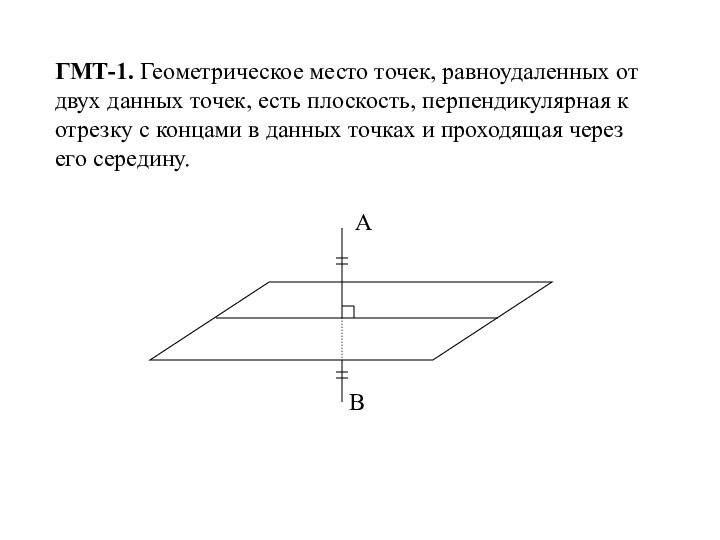

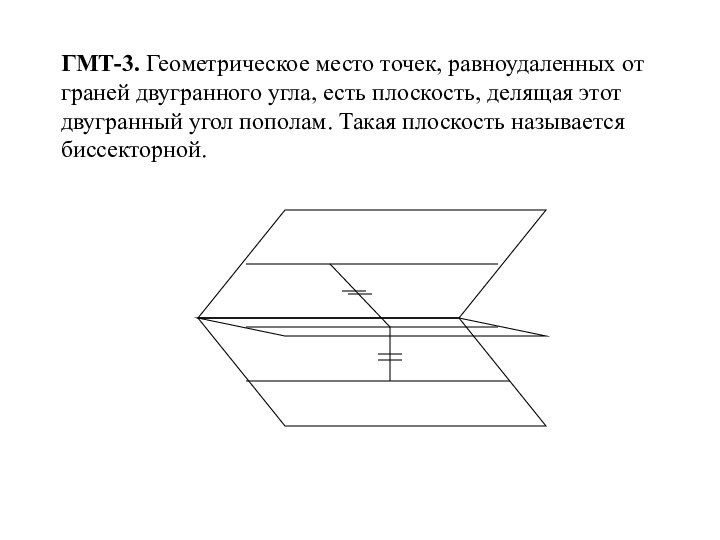











Слайд 3 ГМТ-3. Геометрическое место точек, равноудаленных от граней двугранного
угла, есть плоскость, делящая этот двугранный угол пополам. Такая
плоскость называется биссекторной.Слайд 4 ГМТ-4. Геометрическое место точек, равноудаленных от всех точек
окружности, есть прямая, перпендикулярная плоскости этой окружности, проходящая через
ее центр.
Слайд 5
Описанные шары
Сфера называется описанной около многогранника, если на
ней лежат все его вершины.
Центр шара, описанного около многогранника,
лежит в точке пересечения плоскостей, перпендикулярных ко всем ребрам многогранника и проходящих через их середины. Он может находится внутри, на поверхности и вне многогранника.
Слайд 6
Призма вписанная в шар
Теорема. Шар можно описать около
призмы в том и только том случае, если призма
прямая и около ее основания можно описать окружность.Слайд 7 Следствие 1. Центр шара, описанного около прямой призмы,
лежит на середине высоты призмы, проведенной через центр круга,
описанного около основания.Следствие 2. Шар, в частности можно описать:
Около прямой призмы
Около правильной призмы
Около прямоугольного параллелепипеда
Около прямой четырехугольной призмы, у которой сумма противоположных углов равна 180о.
Слайд 8
Пирамида вписана в шар
Теорема. Около пирамиды можно описать
шар в том и только в том случае, если
около ее основания можно описать окружность.Слайд 9 Следствие 1. Центр шара, описанного около пирамиды, лежит
в точке пересечения прямой, перпендикулярной основанию пирамиды, проходящей через
центр окружности, описанной около этого основания, и плоскости, перпендикулярной любому боковому ребру, проведенной через середину этого ребра.Следствие 2. Если боковые ребра пирамиды равны между собой (или равнонаклонены к плоскости основания), то около такой пирамиды можно описать шар.
Следствие 3. Шар, в частности можно описать:
Около треугольной пирамиды
Около правильной пирамиды
Около четырехугольной пирамиды
Слайд 10
Вписанные шары
Сфера называется вписанной в многогранник, если она
касается всех его граней.
Центр шара, вписанного в многогранник, лежит
в точке пересечения биссекторных плоскостей всех двугранных углов многогранника. Он расположен только внутри многогранника.
Слайд 11
Шар вписан в пирамиду
Теорема. Если боковые грани одинаково
наклонены к основанию, то в такую пирамиду можно вписать
шар.Слайд 12 Следствие 1. Центр шара, вписанного в пирамиду, у
которой боковые грани одинаково наклонены к основанию, лежит в
точке пересечения высоты пирамиды с биссектрисой линейного угла любого двугранного угла при основании пирамиды, стороной которой служит высота боковой грани, проведенная из вершины пирамиды.Следствие 2. В правильную пирамиду можно вписать шар.





























